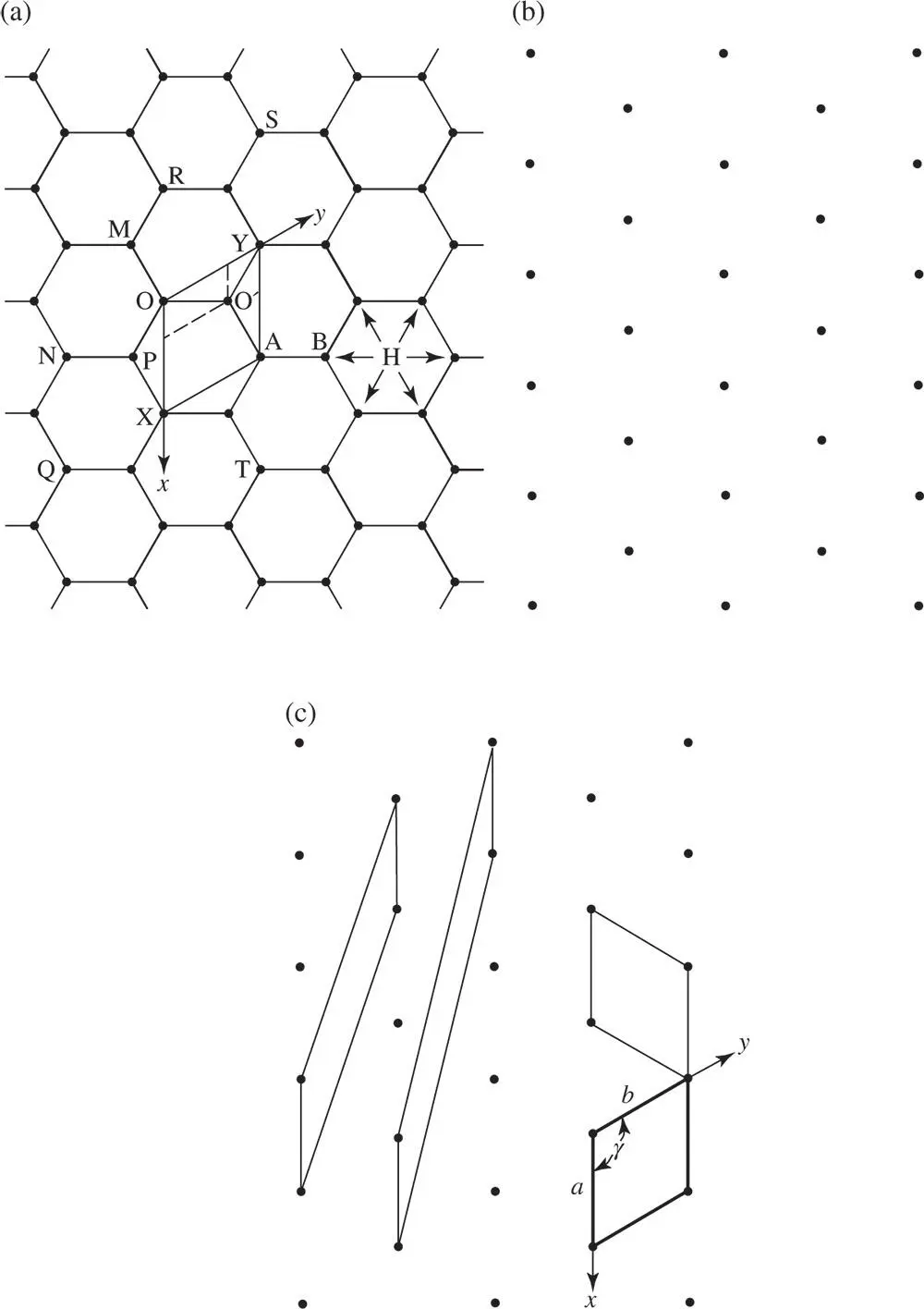
Figure 1.1(a) The arrangement of the atoms in graphene, a single sheet of graphite in which the centre of each atom is represented by a dot, some of which are labelled using capital letters, (b) the lattice of graphene, (c) various choices of primitive unit cells for graphene. In (c), the conventional unit cell is outlined in heavy lines and the corresponding x ‐ and y ‐axes are marked. In (a), H represents the position of an axis of six-fold rotational symmetry (see Section 1.4.2)
It is obvious that we can describe the whole arrangement of atoms and interatomic bonds shown in Figure 1.1a by choosing a small unit such as OXAY, describing the arrangement of the atoms and bonds within it, then moving the unit so that it occupies the position NQXO and repeating the description and then moving it to ROYS and so on, until we have filled all space with identical units and described the whole pattern. If the repetition of the unit is understood to occur automatically, then to describe the crystal we need only describe the arrangement of the atoms and interatomic bonds within one unit. The unit chosen we would call the ‘unit parallelogram’ in two dimensions (in three dimensions, the ‘unit cell’). In choosing the unit we always choose a parallelogram in two dimensions or a parallelepiped in three dimensions. The reason for this will become clear later.
Having chosen the unit, we describe the positions of the atoms inside it by choosing an origin O and taking axes O x and O y parallel to the sides, so that the angle between O x and O y is ≥90°. We state the lengths of the sides a and b , taking a equal to the distance OX and b equal to the distance OY ( Figure 1.1a), and we give the angle γ between O x and O y . In this case a = b = 2.45 Å 1(at 25 °C) and γ = 120°. To describe the positions of the atoms within the unit parallelogram, we note that there is one at each corner and one wholly inside the cell. The atoms at O, X, A and Y all have identical surroundings. 2
In describing the positions of the atoms we take the sides of the parallelogram, a and b , as units of length. Then the coordinates of the atom at O are (0, 0); those at X (1, 0); those at Y (0, 1); and those at A (1, 1). The coordinates of the atom at O′ are obtained by drawing lines through O′ parallel to the axes O x and O y . The coordinates of O′ are therefore 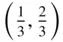 . To describe the contents fully inside the unit parallelogram – that is, to describe the positions of the atoms – we need only give the coordinates of the atom at the origin, (0, 0), and those of the atom at O′. The reason is that the atoms at X, A and Y have identical surroundings to those at O and an atom such as O, X, A or Y is shared between the four cells meeting at these points. The number of atoms contained within the area OXAY is two. O′ is within the area, giving one atom. O, X, A and Y provide four atoms each shared between four unit cells, giving an additional
. To describe the contents fully inside the unit parallelogram – that is, to describe the positions of the atoms – we need only give the coordinates of the atom at the origin, (0, 0), and those of the atom at O′. The reason is that the atoms at X, A and Y have identical surroundings to those at O and an atom such as O, X, A or Y is shared between the four cells meeting at these points. The number of atoms contained within the area OXAY is two. O′ is within the area, giving one atom. O, X, A and Y provide four atoms each shared between four unit cells, giving an additional 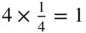 . A second way of arriving at the same result is to move the origin of the unit cell slightly away from the centre of the atom at O so that the coordinate of the O atom is (ε 1, ε 2) and the coordinate of the O′ atom is
. A second way of arriving at the same result is to move the origin of the unit cell slightly away from the centre of the atom at O so that the coordinate of the O atom is (ε 1, ε 2) and the coordinate of the O′ atom is 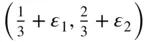 , where 0 < ε 1, ε 2≪ 1. Under these circumstances the centres of the atoms at X, A and Y lie outside the unit cell, so that the atom count within the unit cell is simply two. We note that the minimum number of atoms which a unit parallelogram could contain in a sheet of graphene is two, since the atoms at O and O′ have different environments.
, where 0 < ε 1, ε 2≪ 1. Under these circumstances the centres of the atoms at X, A and Y lie outside the unit cell, so that the atom count within the unit cell is simply two. We note that the minimum number of atoms which a unit parallelogram could contain in a sheet of graphene is two, since the atoms at O and O′ have different environments.
To describe the atomic positions in Figure 1.1a we chose OXAY as one unit parallelogram. We could equally well have chosen OXTA. The choice of a particular unit parallelogram or unit cell is arbitrary, subject to the constraint that the unit cell tessellates, that is, it repeats periodically, in this case in two dimensions. Therefore, NQPM is not a permissible choice – although NQPM is a parallelogram, it cannot be repeated to produce the graphene structure because P and M have environments which differ from those at N and Q.
The corners of the unit cell OXAY in Figure 1.1a all possess identical surroundings. We could choose and mark on the diagram all points with surroundings identical to those at O, X, A and so on. Such points are N, Q, R, S and so on. The array of all such points with surroundings identical to those of a given point we call the mesh or net in two dimensions (a lattice in three dimensions). Each of the points is called a lattice point.
A formal definition of the lattice is as follows: A lattice is a set of points in space such that the surroundings of one point are identical with those of all the others. The type of symmetry described by the lattice is referred to as translational symmetry . The lattice of the graphene crystal structure drawn in Figure 1.1a is shown in Figure 1.1b. It consists of a set of points with identical surroundings. Just a set of points: no atoms are involved. Various primitive unit cells are marked in Figure 1.1c. A primitive unit cell is defined as a unit parallelogram which contains just one lattice point. The conventional unit cell for graphene corresponding to OXAY in Figure 1.1a is outlined in Figure 1.1c in heavy lines and the corresponding x ‐ and y ‐axes are marked.
In general, the conventional primitive unit cell of a two‐dimensional net which shows no obvious symmetry is taken with its sides as short and as nearly equal as possible, with γ , the angle between the x ‐ and y ‐axes, taken to be obtuse, if it is not equal to 90°. However, the symmetry of the pattern must always be taken into account. The net shown in Figure 1.1b is very symmetric and in this case we can take the sides to be equal, so that a = b and γ = 120°.
Comparisons of Figures 1.1a and b emphasize that the choice of the origin for the lattice is arbitrary. If we had chosen O′ in Figure 1.1a as the origin instead of O and then marked all corresponding points in Figure 1.1a, we would have obtained the identical lattice with only a change of origin. The lattice then represents an essential aspect of the translational symmetry of the crystal however we choose the origin.
In three dimensions the definition of the lattice is the same as in two dimensions. The unit cell is now the parallelepiped containing just one lattice point. The origin is taken at a corner of the unit cell. The sides of the unit parallelepiped are taken as the axes of the crystal, x , y , z , using a right‐handed notation. The angles α , β , γ between the axes are called the axial angles (see Figure 1.2). The smallest separations of the lattice points along the x ‐, y ‐ and z ‐axes are denoted by a , b , c , respectively and called the lattice parameters.
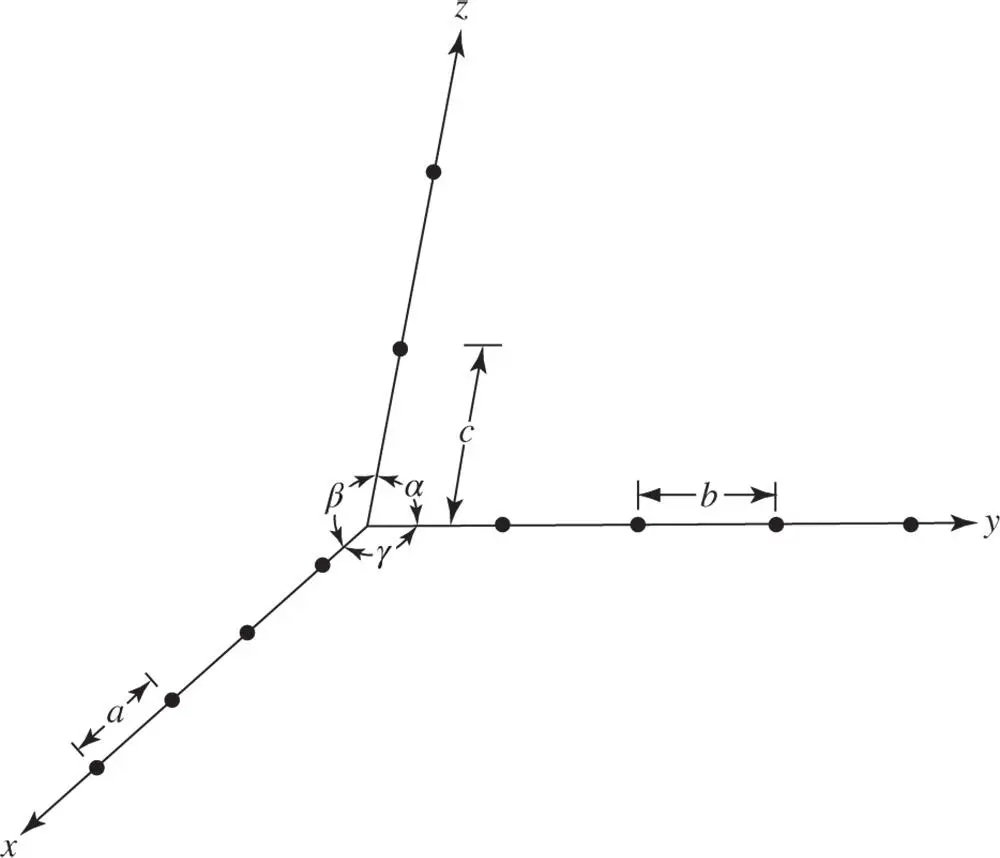
Figure 1.2Definition of the smallest separations a , b and c of the lattice points along the x ‐, y ‐ and z ‐axes respectively, together with the angles α , β and γ between the axes for a lattice in three dimensions
Читать дальше


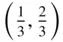 . To describe the contents fully inside the unit parallelogram – that is, to describe the positions of the atoms – we need only give the coordinates of the atom at the origin, (0, 0), and those of the atom at O′. The reason is that the atoms at X, A and Y have identical surroundings to those at O and an atom such as O, X, A or Y is shared between the four cells meeting at these points. The number of atoms contained within the area OXAY is two. O′ is within the area, giving one atom. O, X, A and Y provide four atoms each shared between four unit cells, giving an additional
. To describe the contents fully inside the unit parallelogram – that is, to describe the positions of the atoms – we need only give the coordinates of the atom at the origin, (0, 0), and those of the atom at O′. The reason is that the atoms at X, A and Y have identical surroundings to those at O and an atom such as O, X, A or Y is shared between the four cells meeting at these points. The number of atoms contained within the area OXAY is two. O′ is within the area, giving one atom. O, X, A and Y provide four atoms each shared between four unit cells, giving an additional 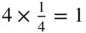 . A second way of arriving at the same result is to move the origin of the unit cell slightly away from the centre of the atom at O so that the coordinate of the O atom is (ε 1, ε 2) and the coordinate of the O′ atom is
. A second way of arriving at the same result is to move the origin of the unit cell slightly away from the centre of the atom at O so that the coordinate of the O atom is (ε 1, ε 2) and the coordinate of the O′ atom is 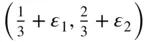 , where 0 < ε 1, ε 2≪ 1. Under these circumstances the centres of the atoms at X, A and Y lie outside the unit cell, so that the atom count within the unit cell is simply two. We note that the minimum number of atoms which a unit parallelogram could contain in a sheet of graphene is two, since the atoms at O and O′ have different environments.
, where 0 < ε 1, ε 2≪ 1. Under these circumstances the centres of the atoms at X, A and Y lie outside the unit cell, so that the atom count within the unit cell is simply two. We note that the minimum number of atoms which a unit parallelogram could contain in a sheet of graphene is two, since the atoms at O and O′ have different environments.











