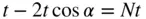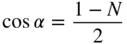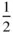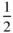(1.21) 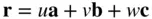
where u , v , w are positive or negative integers, or equal to zero. Inspection of Figure 1.11shows that to use this description we must be careful to choose a, band cso as to include all lattice points. We do this by, say, making athe shortest vector between lattice points in the lattice, or one of several shortest ones. We then choose bas the shortest not parallel to aand cas the shortest not coplanar with aand b. Thus a, band cdefine a primitive unit cell of the lattice in the same sense as in Section 1.1. Only one lattice point is included within the volume a· [ b× c], 7which is the volume of the primitive unit cell; under these circumstances a, band care called the lattice translation vectors.
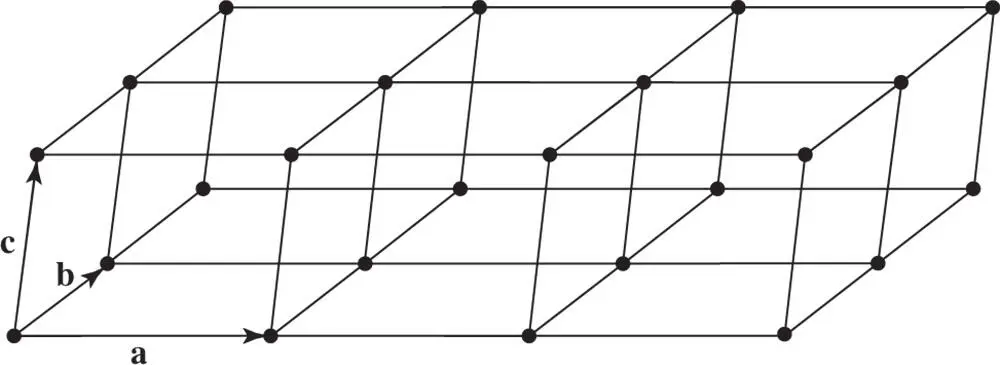
Figure 1.11Translation symmetry in a crystal
1.4.2 Rotational Symmetry
If one stood at the point marked H in Figure 1.1a and regarded the surroundings in a particular direction, say that indicated by one of the arrows, then on turning through an angle of 60° = 360°/6 the outlook would be identical. We say an axis of sixfold rotational symmetry passes normal to the paper through the point H. Similarly, at O′ an axis of threefold symmetry passes normal to the paper, since an identical outlook is found after a rotation of 360°/3 = 120°. A crystal possesses an n ‐fold axis of rotational symmetry if it coincides with itself upon rotation about the axis of 360°/ n = 2 π / n radians. In crystals, axes of rotational symmetry with values of n equal to one, two, three, four and six are the only ones found which are compatible with translational symmetry. These correspond to repetition every 360°, 180°, 120°, 90° and 60° and are called monad, diad, triad, tetrad and hexad axes, respectively. The reasons for these limitations on the value of n are explained in Section 1.5.
A centre of symmetry is a point where inversion through that point produces an identical arrangement. The operation of inversion moves the point with coordinates ( x , y , z ) to the position (− x , − y , − z ). For instance, in Figure 1.3(see also Figure 3.17), if we stood at the centre of the unit cell (coordinates 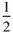 ,
, 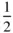 ,
, 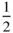 ) and looked in any direction [ uvw ], we would find an identical outlook if we looked in the direction
) and looked in any direction [ uvw ], we would find an identical outlook if we looked in the direction 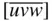 . Clearly, in a lattice, all lattice points are centres of symmetry of the lattice. This follows from Eq. (1.21), since u , v , w can be positive or negative. Of course, since the origin of a set of lattice points can be arbitrarily chosen in a given crystal structure, we must not assume that, in a given crystal with a centre of symmetry, the centres of symmetry necessarily lie where we have chosen to place the lattice points.
. Clearly, in a lattice, all lattice points are centres of symmetry of the lattice. This follows from Eq. (1.21), since u , v , w can be positive or negative. Of course, since the origin of a set of lattice points can be arbitrarily chosen in a given crystal structure, we must not assume that, in a given crystal with a centre of symmetry, the centres of symmetry necessarily lie where we have chosen to place the lattice points.
1.4.4 Reflection Symmetry
The fourth symmetry is reflection symmetry. The operation is that of reflection in a mirror. Mirror symmetry relates, for example, our left and right hands. The dotted plane running normal to the paper, marked m in Figure 1.12, reflects object A to A′, and vice versa. A′ cannot be moved about in the plane of the paper and made to superpose on A. The dotted plane is a mirror plane. It should be noted that the operation of inversion through a centre of symmetry also produces a right‐handed object from a left‐handed one.
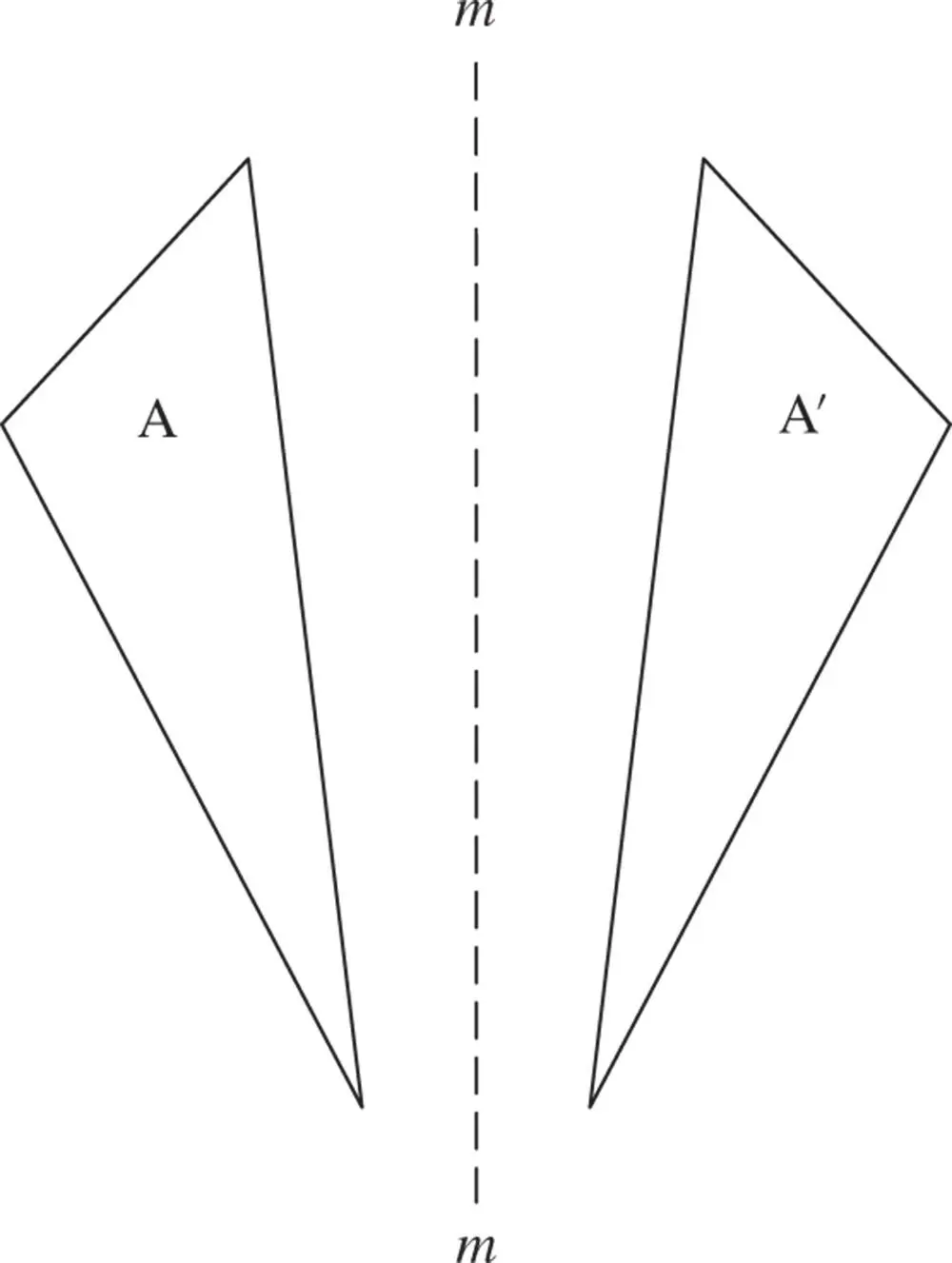
Figure 1.12Reflection symmetry
1.5 Restrictions on Symmetry Operations
All crystals show translational symmetry. 8A given crystal may, or may not, possess other symmetry operations. Axes of rotational symmetry must be consistent with the translational symmetry of the lattice. A onefold rotation axis is obviously consistent. To prove that in addition only diads, triads, tetrads and hexads can occur in a crystal, we consider just a two‐dimensional lattice or net.
Let A, A′, A″, … in Figure 1.13be lattice points of the mesh and let us choose the direction AA′A″ so that the lattice translation vector tof the mesh in this direction is the shortest lattice translation vector of the net. Suppose an axis of n ‐fold rotational symmetry runs normal to the net at A. Then the point A′ must be repeated at B by an anticlockwise rotation through an angle α = A′AB = 2 π / n . Also, since A′ is a lattice point exactly similar to A, there must be an n ‐fold axis of rotational symmetry passing normal to the paper through A′. This repeats A at B′ through a clockwise rotation, as shown in Figure 1.13. That these two rotations are in opposite senses does not matter – they are both a consequence of the n ‐fold axis of rotational symmetry under consideration.
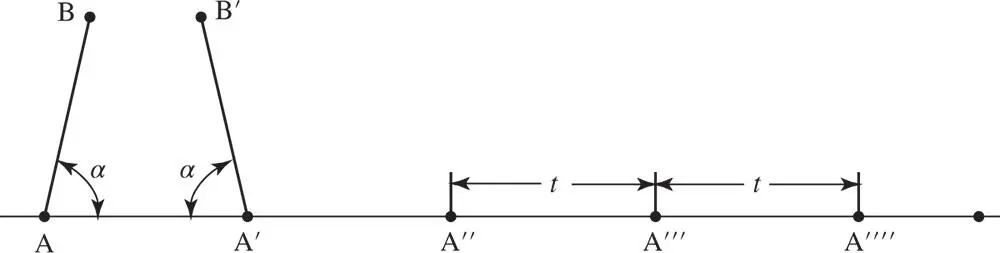
Figure 1.13Diagram to help determine which rotation axes are consistent with translational symmetry
B and B′ define a lattice row parallel to AA′. Therefore, the separation of B and B′ by Eq. (1.12) must be an integral number times t. Call this integer N . From Figure 1.13the separation of B and B′ is ( t − 2 t cos α ). Therefore, the possible values of α are restricted to those satisfying the equation:
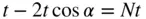
or:
(1.22) 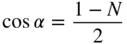
where N is an integer. Since −1 ≤ cos α ≤ 1 the only possible solutions are shown in Table 1.1. These correspond to onefold, sixfold, fourfold, threefold, and twofold axes of rotational symmetry. No other axis of rotational symmetry is consistent with the translational symmetry of a lattice and hence other axes do not occur in crystals. 9
Table 1.1Solutions of Eq. (1.22)
| N |
−1 |
0 |
1 |
2 |
3 |
| cos α |
1 |
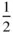 |
0 |
− 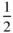 |
−1 |
| α |
0° |
60° |
90° |
120° |
180° |
Corresponding to the various allowed values of α derived from Eq. (1.22), three two‐dimensional lattices, also known as nets or meshes, are defined. These are shown as the first three diagrams on the left‐hand side of Figure 1.14. It should be noted that the hexad axis and the triad axis both require the same triequiangular mesh, the unit cell of which is a 120° rhombus (see Figure 1.14c).
Читать дальше

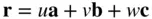

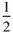 ,
, 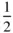 ,
, 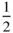 ) and looked in any direction [ uvw ], we would find an identical outlook if we looked in the direction
) and looked in any direction [ uvw ], we would find an identical outlook if we looked in the direction 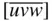 . Clearly, in a lattice, all lattice points are centres of symmetry of the lattice. This follows from Eq. (1.21), since u , v , w can be positive or negative. Of course, since the origin of a set of lattice points can be arbitrarily chosen in a given crystal structure, we must not assume that, in a given crystal with a centre of symmetry, the centres of symmetry necessarily lie where we have chosen to place the lattice points.
. Clearly, in a lattice, all lattice points are centres of symmetry of the lattice. This follows from Eq. (1.21), since u , v , w can be positive or negative. Of course, since the origin of a set of lattice points can be arbitrarily chosen in a given crystal structure, we must not assume that, in a given crystal with a centre of symmetry, the centres of symmetry necessarily lie where we have chosen to place the lattice points.