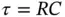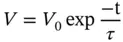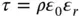Table 2.2Approximate capacitance of typical everyday objects.
| Electronic components and small assemblies |
0.1–30 pF |
| Drinks can, small metal parts |
10–20 pF |
| Tweezers held in hand |
25 pF |
| Small metal containers (1–50 l), trolleys |
10–100 pF |
| Larger metal containers (250–500 l) |
50–300 pF |
| Human body |
100–300 pF |
| Small signal MOSFET gate capacitance |
100 pF |
| Power MOSFET gate‐source capacitance |
900–1200 pF |
| Car |
800–1200 pF |
MOSFET, Metal Oxide Silicon Field Effect Transistor
A corollary of this is that the voltage and field surrounding a charged object may be suppressed by the presence of a nearby conducting object. If the capacitance of the system is increased, the voltage is decreased.
As an example, a charged garment that fits snugly to the body has voltage suppressed due to the proximity of its surfaces to the body. Even if the garment is highly charged, the external field may be limited due to this. If the garment flaps open, the body and garment surfaces move apart. “Capacitance” is reduced, and a high voltage and electrostatic field appears outside the garment.
The resistance and capacitance form a resistor‐capacitor (RC) network that has a characteristic time constant τ .
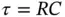
In a time τ , the voltage will decay to about 37% of its initial value.
In the example, if the charge current is suddenly halted at time t = 0 with initial voltage V 0, the voltage V on the capacitor reduces as
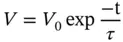
An electrostatic field meter monitoring the material surface would measure this exponential decay of voltage. The product of a material's resistivity ρ and permittivity ɛ 0 ɛ rgives a physical time constant for the material.
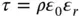
This behavior has important practical implications. If we consider a situation in which the capacitance is fixed at 100 pF (the order of magnitude of capacitance of a person) and the charging current 100 nA, we can consider the effect of different resistances. With a resistance of 1 GΩ, the voltage generated is only 100 V, and on cessation of the current, the voltage will fall to 37% of its initial value within 10 9× 10 −10= 0.1 seconds. The effect of a short duration charging current of this magnitude is unlikely to be noticed.
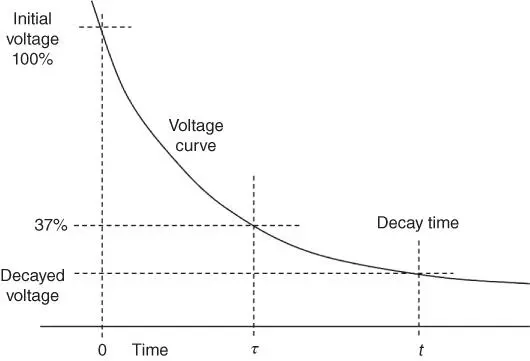
Figure 2.3Charge or voltage decay curve.
If the resistance is increased 10 GΩ, not only is the voltage generated increased to 1 kV, but on cessation of the current, the voltage will take 10 10× 10 −10= 1 seconds to fall to 37% of its initial value. The presence of this voltage may or may not be noticeable or cause a problem, depending on the circumstance.
If the resistance is increased 100 GΩ, not only is the voltage generated increased to 10 kV, but on cessation of the current, the voltage will take 10 seconds to fall to 37% of its initial value. The presence of this voltage for such a long time could lead to the person experiencing shocks on touching something or discharging to cause some problem.
In ESD control, a different definition of charge decay time is usually used in standard measurements, and often the time for charge to reduce to one‐tenth of its initial value is measured ( Figure 2.3). This value is theoretically equal to 2.3 τ .
In practice, the charge decay time is often measured from the starting voltage down to a certain threshold voltage, e.g. 100 V. Polymers may have time constants of many tens or hundreds of seconds, or even days under clean dry conditions.
In practice, the simple model does not always correspond well with material behavior. Measured charge decay curve may depart considerably from the ideal exponential, and the measured time “constant” varies with measurement conditions. Often with high resistance materials the decay time lengthens as the surface voltage drops and may become very long at low voltages.
2.3.4 Conductors and Insulators Revisited
In many engineering fields, conductors are often thought of as materials such as copper or aluminum that have very low resistance or resistivity (see Section 1.7), much less than 1 Ω. In ESD control, materials that have a much higher resistivity than this may be thought of as conductors. In practical electrostatic control, materials and equipment are often defined as conductors or insulators based on either a measured resistance or a charge decay time, or both. The model of Figure 2.1can be used to explain this.
As charge generation rate (current I ) in static electricity is often low, even a relatively high value of leakage resistance R ( Figure 2.1) may pass the current to give low voltage, V = IR . In ESD control, a resistance of 1 MΩ (10 6Ω) could be considered quite conductive and would reduce the electrostatic voltage in the previous example to 1 V. As an example, in a case where the charge generation currents normally experienced in practice are expected to be no more than 1 nA, calculations can be made on this basis. Alongside this, it may be wished to limit voltages to some level, e.g. 100 V. Given these constraints, the model and Ohm's law show that resistances up to V / I = 10 2/10 −9= 10 11Ω would be acceptable.
In an application (e.g. electrostatic hazards avoidance in industrial processes) where higher charge generation is expected, the allowable resistance may be considerably smaller (IEC 60079‐32‐1).
A second way of looking at the matter is to decide how long a transient charge built up on a material or object may tolerably be allowed to remain without problems occurring. This may be evaluated in terms of the charge decay time. If a conductor has capacitance around 10 pF, resistance to ground of 10 11Ω will give a charge decay time of one second, and in the absence of charge generation a stored charge will reduce to only 5% of its initial value within three seconds. In manual assembly and handling processes, this will usually be fast enough to avoid problems. For materials, this decay time corresponds to a permittivity of 10 −11Fm −1and resistivity of 10 11Ω. The permittivity of air is around 0.9 × 10 −11Fm −1, and many plastics are around 2 × 10 −11Fm −1. The presence of higher capacitance or material permittivity, or a requirement for faster charge decay, may lead to a lower maximum acceptable resistance.
2.3.5 The Effect of Relative Humidity
Water is an electrically conducting material. Moisture from the air forms a thin layer on the surface of many materials and can contribute to their apparent electrical conductivity. Some materials, especially natural materials such as paper, reduce by orders of magnitude in their resistivity as relative humidity increases from dry conditions.
As material surface resistance is increased under dry conditions, electrostatic charge build‐up is often greatly enhanced. Some ESD control materials use additives to attract moisture to a polymer surface and provide static dissipative behavior. These materials may not work well at low humidity. As a rule of thumb, electrostatic charge build‐up is generally increased for humidity less than about 30% rh.
Читать дальше