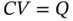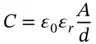Jeremy M. Smallwood - The ESD Control Program Handbook

In practice, triboelectrification is a variable phenomenon and is highly dependent on surface conditions, contaminants, and humidity. Small amounts of surface contaminants can have a large effect on triboelectrification. One result is that the order of triboelectric series is not unique. Different experiments and samples of the same materials may produce different results especially if the experimental conditions are varied. While it could be assumed from the triboelectric series that contact between two surfaces of the same material would not generate charge, this is generally not what happens in practice.

Any two materials in contact give charge separation that can lead to static electrical charge build‐up. This may or may not lead to charge and voltage build‐up, depending on the circumstances.

The key to this build‐up is the balance between charge generation and charge dissipation (or neutralization). If charge is dissipated (or neutralized) more quickly than it is generated, no static electricity builds up, and no effects are noticed. If charge is generated more quickly than it is dissipated (or neutralized), then high voltages and static electricity effects are quickly built up.

Table 2.1An example of a triboelectric series.

Static electricity can be modeled as a charge generator, and a simple electrical model can be used to understand many practical situations ( Figure 2.1).

The separation of charge is effectively a small electrical current represented by a current source I . The capacitor C represents the charge storage properties of the system and could be a material surface or a conducting object with a capacitance to earth. The resistance R represents charge dissipation processes (other than ESD) and can vary from less than 1 Ω to more than 10 14Ω for good insulators. (See Sections 1.7.3 and 2.3.4 for discussions on the meaning of insulators and conductors.)

If the current is constant (i.e. the effect of capacitance can be neglected), it's easy to see by Ohm's law that the voltage developed is highly dependent on the resistance R . If a charge generation rate of 1 nA (1 nCs −1) is present, with a resistance of 10 9Ω, a steady state voltage of 1 V is produced. If, however, the resistance was 10 12Ω, a voltage of 1 kV would be produced, and for a resistance of 10 14Ω, a voltage of 100 kV would theoretically be produced! For a charge generation rate of 1 μA, a resistance of 10 10Ω would yield a voltage of 10 kV. In practice, electrostatic sources rarely generate charge at this rate or on a steady current basis unless there is steady movement involved (e.g. in a conveyor system).

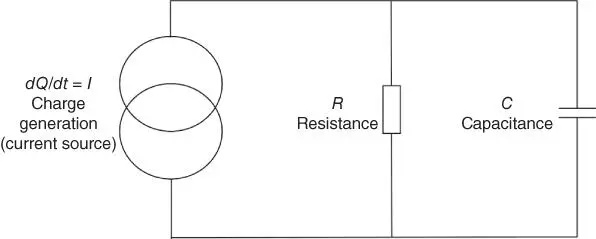
Figure 2.1A simple electrical model of electrostatic charge build‐up.

The rate of electrostatic charge generation is affected by many factors. Some of the key factors are as follows:

Relative position of the materials in the triboelectric series

Rate of separation of contact area (high rates of movement)

Condition of the surfaces that make contact

Rubbing of the contacting surfaces

Ambient humidity and temperature

The many factors involved in triboelectric charge separation make it a highly unpredictable phenomenon.

The capacitance C represents charge storage. There is a simple relation between charge Q and voltage V , and capacitance is the ratio of charge and voltage.

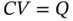
In practice, capacitance is usually a variable that depends on the materials and nearby objects and on the proximity to earth. Objects move around in daily life, and so their capacitance changes.

As an example, we can consider the human body. It is, in electrostatic terms, a conducting object, being mainly composed of water, which is a conducting material. Even if we neglect the nearby objects and earth, the human body can be approximated as a sphere that has a similar surface area. The “free space” capacitance of a sphere is given by 4πɛ 0 r , where r is the radius and ɛ 0is the permittivity of free space, 8.8 × 10 −12Fm −1. Typically, a 1 m radius sphere gives a useful approximation and has a “free space” capacitance around 110 pF.

Figure 2.2Parallel plate capacitor.

Nearby objects and earth increase this value. In fact, the human feet, on the earth, approximate two parallel plate capacitors in parallel with the free space capacitance. Each capacitor is made up of two electrodes: the sole of the foot and the earth. These are separated by a layer of material (the shoe sole, typically an insulating polymer of relative permittivity ɛ raround 2.5). Each foot capacitance varies from moment to moment as the feet are lifted and replaced on the ground during walking. Each foot capacitance can be modeled as a parallel plate capacitor ( Figure 2.2), with plates of area A separated by a distance d and capacitance C given by

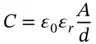
In general, if either the area A or the distance of separation d are changed, then the capacitance will change. If the charge is held constant, increasing the capacitance will decrease the body voltage, and reducing capacitance will increase body voltage. Reducing capacitance can be achieved by reducing the area (e.g. standing on tip‐toe) or increasing the separation distance (e.g. raising the foot from the floor).

The previous equation shows that if the charge on conductor is unchanged and the capacitance changes, then the voltage of the conductor changes. For example, if a person's body capacitance changes between 50 and 150 pF while walking and the charge on their body is constant at 5 nC, their body voltage will vary between 100 V (at 50 pF) and 33 V (at 150 pF). If a printed circuit board (PCB) conductor has a capacitance of 20 pF and charge 5 nC when resting close to a large earthed machine part, its voltage will be 250 V. If its capacitance is reduced to 5 pF when far away from this machine part, its voltage will rise to 1000 V.

It can be useful to have an idea of the approximate capacitance of everyday objects, especially when estimating the possible effect of ESD to or from such items. Table 2.2gives some examples (IEC 61340‐1).

The variable ratio between charge and voltage behaves similarly for nonconductors.

When seated in a chair, the body generates charge on the clothes surfaces in contact with the chair. This forms a large area of charged material with a small distance between the charges (the two surfaces are in contact). The person's body voltage is low in this situation even though their clothing may be highly charged. On rising from the chair, the person can take much of the separated charge with them. The effective “capacitance” between the body and the chair is rapidly reduced (separation is rapidly increased), and a high body voltage quickly results if the charge cannot dissipate to ground. It is common to feel a shock on touching something metal after rising from a chair or car seat – voltages over 10 kV have been measured on people after getting out of a car seat (Pirici et al. 2003; Andersson et al. 2014).