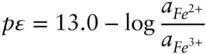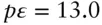The greater the p ε, the greater the tendency of species to lose their transferable, or valence, electrons. In a qualitative way, we can think of the negative of pε as a measure of the availability of electrons. pε can be related in a general way to the relative abundance of electron acceptors. When an electron acceptor, such as oxygen, is abundant relative to the abundance of electron donors, the pε is high and electron donors will be in electron-poor valence states (e.g., Mn 4+instead of Mn 2+). pε , and E H, are particularly useful concepts when combined with pH to produce diagrams representing the stability fields of various species. We will briefly consider how these are constructed.
pε –pH and E H–pH diagrams are commonly used tools of aqueous geochemistry, and it is important to become familiar with them. An example, the pε –pH diagram for iron, is shown in Figure 3.19. pε –pH diagrams look much like phase diagrams, and indeed there are many similarities. There are, however, some important differences. First, labeled regions do not represent conditions of stability for phases; rather they show which species will predominate under the pε –pH conditions within the regions. Indeed, in Figure 3.19we consider only a single phase: an aqueous solution. The bounded regions are called predominance areas . Second, species are stable beyond their region: boundaries represent the conditions under which the activities of species predominating in two adjoining fields are equal . However, since the plot is logarithmic, activities of species decrease rapidly beyond their predominance areas.
More generally, a pε –pH diagram is a type of activity or predominance diagram , in which the region of predominance of a species is represented as a function of activities of two or more species or ratios of species. We will meet variants of such diagrams in later chapters.
Let's now see how Figure 3.19can be constructed from basic chemical and thermodynamic data. We will consider only a very simple Fe-bearing aqueous solution. Thus, our solution contains only species of iron, the dissociation products of water and species formed by reactions between them. Thermodynamics allow us to calculate the predominance region for each species. To draw boundaries on this plot, we will want to obtain equations in the form of p ε = a + b × pH. With an equation in this form, b is a slope and a is an intercept on a pε–pH diagram. Hence we will want to write all redox reactions so that they contain e –and all acid–base reactions so that they contain H +.
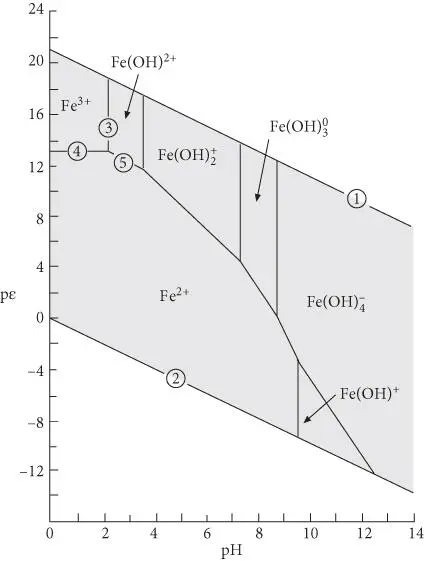
Figure 3.19 p ε–pH diagram showing predominance regions for ferric and ferrous iron and their hydrolysis products in aqueous solution at 25°C and 0.1 MPa.
In Figure 3.18, we are only interested in the region where water is stable. So to begin construction of our diagram, we want to draw boundaries outlining the region of stability of water. The upper limit is the reduction of oxygen to water:
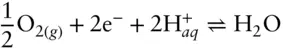
The equilibrium constant for this reaction is:
(3.117) 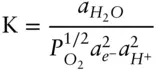
Expressed in log form:
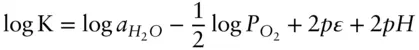
The value of log K is 41.56 (at 25°C and 0.1 MPa). In the standard state, the activity of water and partial pressure of oxygen are 1 so that 3.117 becomes:
(3.118) 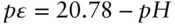
Equation 3.118plots on a pε –pH diagram as a straight line with a slope of −1 intersecting the vertical axis at 20.78. This is labeled as line ➀ on Figure 3.19.
Similarly, the lower limit of the stability of water is the reduction of hydrogen:
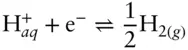
Because Δ G° r= 0 and log K = 0 (by convention), we have pε = −pH for this reaction: a slope of 1 and intercept of 0. This is labeled as line ➁ on Figure 3.19. Water is stable between these two lines (region shown in gray on Figure 3.19).
Now let's consider the stabilities of a few simple aqueous iron species. One of the more important reactions is the hydrolysis of Fe 3+:
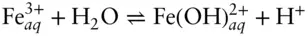
The equilibrium constant for this reaction is 0.00631. The equilibrium constant expression is then:
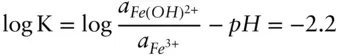
Region boundaries on pε–pH diagrams represent the conditions under which the activities of two species are equal. When the activities of FeOH 2+and Fe 3+are equal, the equation reduces to:
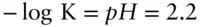
Thus, this equation defines the boundary between regions of predominance of Fe 3+and Fe(OH) 2+. The reaction is independent of pε (no oxidation or reduction is involved), and it plots as a straight vertical line pH = 2.2 (line ➂ on Figure 3.19). Boundaries between the successive hydrolysis products, such as 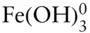 and
and 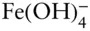 , can be similarly drawn as vertical lines at the pH equal to their equilibrium constants, and occur at pH values of 3.5, 7.3, and 8.8. The boundary between Fe 2+and Fe(OH) –can be similarly calculated and occurs at a pH of 9.5.
, can be similarly drawn as vertical lines at the pH equal to their equilibrium constants, and occur at pH values of 3.5, 7.3, and 8.8. The boundary between Fe 2+and Fe(OH) –can be similarly calculated and occurs at a pH of 9.5.
Now consider equilibrium between Fe 2+and Fe 3+( eqn. 3.102). The pε° for this reaction is 13.0 ( Table 3.3), hence from eqn. 3.112we have:
(3.119) 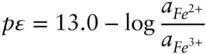
When the activities are equal, this equation reduces to:
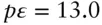
and therefore plots as a horizontal line at pε = 13 that intersects the FeOH 2+–Fe 3+line at an invariant point at pH = 2.2 (line ➃ on Figure 3.19).
Читать дальше


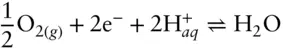
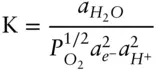
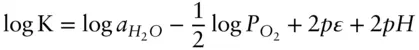
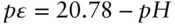
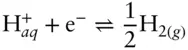
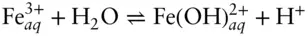
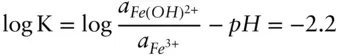
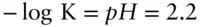
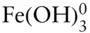 and
and 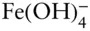 , can be similarly drawn as vertical lines at the pH equal to their equilibrium constants, and occur at pH values of 3.5, 7.3, and 8.8. The boundary between Fe 2+and Fe(OH) –can be similarly calculated and occurs at a pH of 9.5.
, can be similarly drawn as vertical lines at the pH equal to their equilibrium constants, and occur at pH values of 3.5, 7.3, and 8.8. The boundary between Fe 2+and Fe(OH) –can be similarly calculated and occurs at a pH of 9.5.