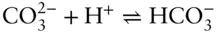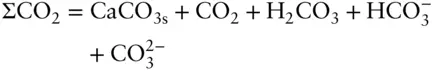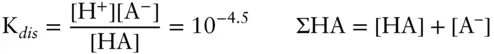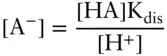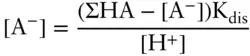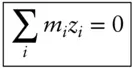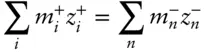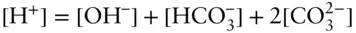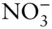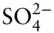This constraint, also sometimes called mole balance , is a very simple one, and as such it is easily overlooked. When a salt is dissolved in water, the anion and cation are added in stoichiometric proportions. If the dissolution of the salt is the only source of these ions in the solution, then for a salt of composition C ν+A ν–we may write:
(3.98) 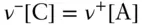
Thus, for example, for a solution formed by dissolution of CaCl 2in water, the concentration of Cl –ion will be twice that of the Ca 2+ion. Even if CaCl 2is not the only source of these ions in solution, its congruent dissolution allows us to write the mass balance constraint in the form of a differential equation:
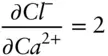
which just says that CaCl 2dissolution adds two Cl –ions to solution for every Ca 2+ion added.
By carefully choosing components and boundaries of our system, we can often write conservation equations for components. For example, suppose we have a liter of water containing dissolved CO 2in equilibrium with calcite (for example, groundwater in limestone). In some circumstances, we may want to choose our system as the water plus the limestone, in which case we may consider Ca conserved and write:
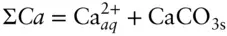
where CaCO 3sis calcite (limestone) and 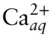 is aqueous calcium ion. We may want to avoid choosing carbonate as a component and choose carbon instead, since the carbonate ion is not conserved because of association and dissociation reactions such as:
is aqueous calcium ion. We may want to avoid choosing carbonate as a component and choose carbon instead, since the carbonate ion is not conserved because of association and dissociation reactions such as:
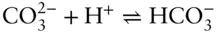
Choosing carbon as a component has the disadvantage that some carbon will be present as organic compounds, which we may not wish to consider. A wiser choice is to define CO 2as a component. Total CO 2would then include all carbonate species as well as CO 2(very often, total CO 2is expressed instead as total carbonate). The conservation equation for total CO 2for our system would be:
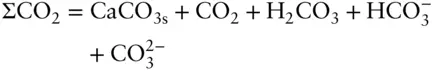
Here we see the importance of the distinction we made between components and species earlier in the chapter.Example 3.9 illustrates the use of mass balance.
Example 3.9Soil organic acid
Consider soil water with a pH of 7 containing a weak organic acid, which we will designate HA, at a concentration of 1 × 10 −4M. If the apparent dissociation constant of the acid is 10 −4.5, what fraction of the acid is dissociated?
Answer: We have two unknowns: the concentration of the dissociated and undissociated acid, and we have two equations: the equilibrium constant expression for dissociation and the mass balance equation. We will have to solve the two simultaneously to obtain the answer. Our two equations are:
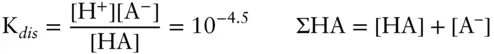
Solving the dissociation constant expression for [A –], we have:
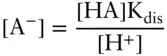
Then solving the conservation equation for [HA] and substituting, we have
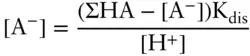
Setting H +to 10 −7and ΣHA to 10 −4, we calculate [A –] as 3.16 × 10 −5M, so 31.6% of the acid is dissociated.
3.10.3 Electrical neutrality
There is an additional condition that electrolyte solutions must meet: electrical neutrality . Thus, the sum of the positive charges in solutions must equal the sum of the negative ones, or:
(3.99) 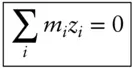
While this presents some experimental obstacles, for example, we cannot add only Na +ion to an aqueous solution while holding other compositional parameters constant; it also allows placement of an additional mathematical constraint on the solution. It
is often convenient to rearrange eqn. 3.99so as to place anions and cations on different sides of the equation:
(3.100) 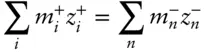
As an example, consider water in equilibrium with atmospheric CO 2and containing no other species. The charge balance equation in this case is:
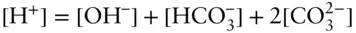
As Example 3.10illustrates, the electrical neutrality constraint can prove extremely useful.
Example 3.10Determining the pH of rainwater from its composition
Determine the pH of the two samples of rain in the adjacent table. Assume that sulfuric and nitric acid are fully dissociated and that the ions in the table, along with H +and OH –, are the only ones present.
| Analysis of rainwater |
|
Rain 1 (μM) |
Rain 2 (μM) |
| Na |
9 |
89 |
| Mg |
4 |
16 |
| K |
5 |
9 |
| Ca |
8 |
37 |
| Cl |
17 |
101 |
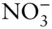 |
10 |
500 |
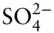 |
18 |
228 |
Answer : This problem is simpler than it might first appear. Given the stated conditions, there are no reactions between these species that we need to concern ourselves with. To solve the problem, we observe that this solution must be electrically neutral: any difference in the sum of cations and anions must be due to one or both of the two species not listed: OH –and H +.
We start by making an initial guess that the rain is acidic and that the concentration of H +will be much higher than that of OH –, and that we can therefore neglect the latter (we will want to verify this assumption when we have obtained a solution). The rest is straightforward. We sum the product of charge times concentration ( eqn. 3.99) for both cations and anions and find that anions exceed cations in both cases: the difference is equal to the concentration of H +. Taking the log of the concentration (having first converted concentrations to M from μM by multiplying by 10 −6), we obtain a pH of 4.6 for the first sample and 3.14 for the second.
Читать дальше

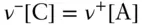
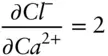
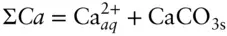
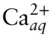 is aqueous calcium ion. We may want to avoid choosing carbonate as a component and choose carbon instead, since the carbonate ion is not conserved because of association and dissociation reactions such as:
is aqueous calcium ion. We may want to avoid choosing carbonate as a component and choose carbon instead, since the carbonate ion is not conserved because of association and dissociation reactions such as: