Dr. Diangelakisis an Optimization Specialist at Octeract Ltd. in London, UK, a massively parallel global optimization software firm. He was a postdoctoral research associate at Texas A&M University and Texas A&M Energy Institute. He holds a PhD and M.Sc. on Advanced Chemical Engineering from Imperial College London and has been a member of the “Multi‐parametric Optimization and Control Group” since late 2011. He earned his bachelor degree in 2011 from the National Technical University of Athens (NTUA). His main research interests are on the area of optimal receding horizon strategies for chemical and energy processes while simultaneously optimizing their design. For that purpose, he is investigating novel solution methods for classes of non‐linear, robust, and multi‐parametric optimization programming problems. He is the main developer of the PARametric Optimization and Control (PAROC) platform and co‐developer of the Parametric OPtimization (POP) toolbox. In 2016 he was chosen as one of five participants in the “Distinguished Junior Researcher Seminars” in Northwestern University, organized by Prof. Fengqi You. In 2017 he received the third place in EFCE's “Excellence Award in Recognition of Outstanding PhD Thesis on CAPE.” He is the coauthor of 16 peer reviewed articles, 11 conference papers and 3 book chapters.
Richard Oberdieckis a Technical Account Manager at Gurobi Optimization, LLC, one of the leading mathematical optimization software companies. He obtained a bachelor and MSc degrees from ETH Zurich in Switzerland (2009–1013), before pursuing a PhD in Chemical Engineering at Imperial College London, UK, which he completed in 2017. During is PhD, he discovered fundamental properties of multi‐parametric programming problems and implemented them in the Parametric Optimization (POP) toolbox, of which he was the main developer. After using his knowledge in mathematical modeling and optimization in the space of renewable energies at the world leader in offshore wind energy, Ørsted A/S, he is now helping companies around the world unlock business value through mathematical optimization as a Technical Account Manager for Gurobi Optimization, LLC. He has published 21 papers and 2 book chapters, has an h‐index of 11 and was awarded the FICO Decisions Award 2019 in Optimization, Machine Learning and AI.
Many optimization problems involve parameters that are unknown, either because they cannot be measured, or because they represent information about the future (e.g. future state of a system, future disturbance, future demand). Multi‐parametric programming is a technique for the solution of such class of uncertain optimization problems. Through multi‐parametric programming, one can obtain the optimization variables of the problem as a function of the bounded uncertain parameters, and the regions (in the space of the parameters) where these functions are valid.
Theoretic and algorithmic developments on multi‐parametric programming, along with applications in the area of process systems engineering, have been constantly emerging during the last 30 years.
A variety of algorithms for the solution of a range of classes of multi‐parametric programming problems have been developed, with our group publishing over 80 manuscripts, 21 books and book chapters, and 2 patents on the subject. We have further developed a MATLAB ©based toolbox, POP ©, for the solution of various classes of multi‐parametric programming and a framework, PAROC ©, for the development of explicit model predictive controllers.
This book aims to enable fundamental understanding in the areas of multi‐parametric optimization and control. We hope that by the end of the book, the reader will be able to not only understand almost all aspects of multi‐parametric programming, but also judge the key characteristics and particulars of the various techniques developed for different mathematical programming problems, use the tools to solve parametric problems, and finally, develop explicit model predictive controllers.
The book begins with an introduction to the fundamentals of optimization and the basic theories and definitions used in multi‐parametric optimization. Then, two main parts follow, providing a clear distinction between algorithmic developments and their applications in the development of explicit model predictive controllers.
Part I focuses on the algorithmic developments of multi‐parametric programming. It begins with an overview of the basic sensitivity theorem and progresses to describe solution strategies for linear, quadratic, and mixed‐integer multi‐parametric problems. A chapter for the solution of the aforementioned classes of problems in MATLAB ©is also included. Part I concludes with developments of multi‐parametric programming for the solution of other classes of problems.
Part II focuses on multi‐parametric model predictive control and its extension for the solution of other control problems. This section concludes with the presentation and applications of PAROC ©framework, a framework for the development and closed loop validation of multi‐parametric model predictive controllers.
As this book is the outcome of the research work carried out over the last 30 years at the Centre for Process Systems Engineering of Imperial College London and the Texas A&M Energy Institute of Texas A&M University, many colleagues, former and current PhD students, and post‐doctorate/research associates have been involved in the presented work. While a number of them are involved in this project as co‐authors, we would like to take the opportunity to thank in particular our current research team at Texas A&M Energy Institute, particularly Dr. Styliani Avraamidou and Mr. Iosif Pappas.
We would also like to gratefully acknowledge the financial support kindly provided by our many sponsors, EPSRC, NSF, EU/ERC, DOE/CESMII, DOE/RAPID, Shell, Air Products, Eli‐Lilly, and BP.
Finally, we would like to thank Wiley‐VCH for their enthusiastic support of this effort.
Richard Oberdieck
College Station, October 2019
Efstratios N. Pistikopoulos
Nikolaos A. Diangelakis
Part I Multi‐parametric Optimization
In this chapter, the fundamental concepts of mathematical optimization and multi‐parametric programming will be presented. Such concepts will be the foundation towards the development of state‐of‐the‐art multi‐parametric programming strategies and applications, which will appear in this book in the next chapters.
1.1 Concepts of Optimization
1.1.1 Convex Analysis
This section presents the idea of convex sets and introduces function convexity. Convexity plays a vital role to establish the required properties which will enable a multi‐parametric solution to hold. In this setting, the following definitions are established.
Consider the points 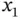 and
and 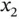
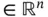 . Then the line that passes through these points is defined as
. Then the line that passes through these points is defined as
(1.1) 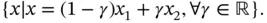
Читать дальше

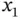 and
and 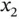
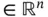 . Then the line that passes through these points is defined as
. Then the line that passes through these points is defined as