If π were set equal to 0.5, then all the distributions corresponding to those of Figure 4.4would be symmetrical whatever the size of n . On the other hand, if π = 0.75 then the distributions would be skewed to the left.
We can use the properties of the Binomial distribution when making inferences about proportions, as we shall see in subsequent chapters.
Example – Probability of Corn Resolving
Farndon et al. (2013) give the successful response rate to scalpel treatment in 94 patients with foot corns as 21%. From their data we have p = 20/94 = 0.21. Suppose a podiatrist treated four patients with corns with scalpel debridement. What is the probability that at most one patient responds to treatment? This implies that either 0 or 1 respond. We can use formula 4.1, with r = 0 to give 1 × 0.21 0× (1–0.21) 4= 0.3895 and with r = 1 to give 4 × 0.21 1× (1–0.21) 3= 0.4142. Summing these two probabilities gives P = 0.3895 + 0.4142 = 0.8037.
4.3 The Poisson Distribution
The Poisson distribution is used to describe discrete quantitative data such as counts that occur independently and randomly in time or space at some average rate. For example, the number of deaths in a town from a particular disease per day, or the number of admissions to a particular hospital in a day typically follows a Poisson distribution.
The Poisson random variable is the count of the number of events that occur independently and randomly in time at some rate, λ. The formula for a Poisson distribution is given as Eq. (4.2)in Section 4.9.
We can use our knowledge of the Poisson distribution to calculate the anticipated number of hospital admissions on any particular day or the number of deaths from lung cancer in a year in a town. We can use this information to compare observed and expected values, to decide if, for example, the number of deaths from cancer in an area is unusually high.
Figure 4.5shows the Poisson distribution for four different rates λ = 1, 4, 10 and 15. For λ = 1 the distribution is very right skewed, for λ = 4 the skewness is much less and as the rate increases to λ = 10 or 15 it is more symmetrical, and looks more like the Binomial distribution in Figure 4.4.
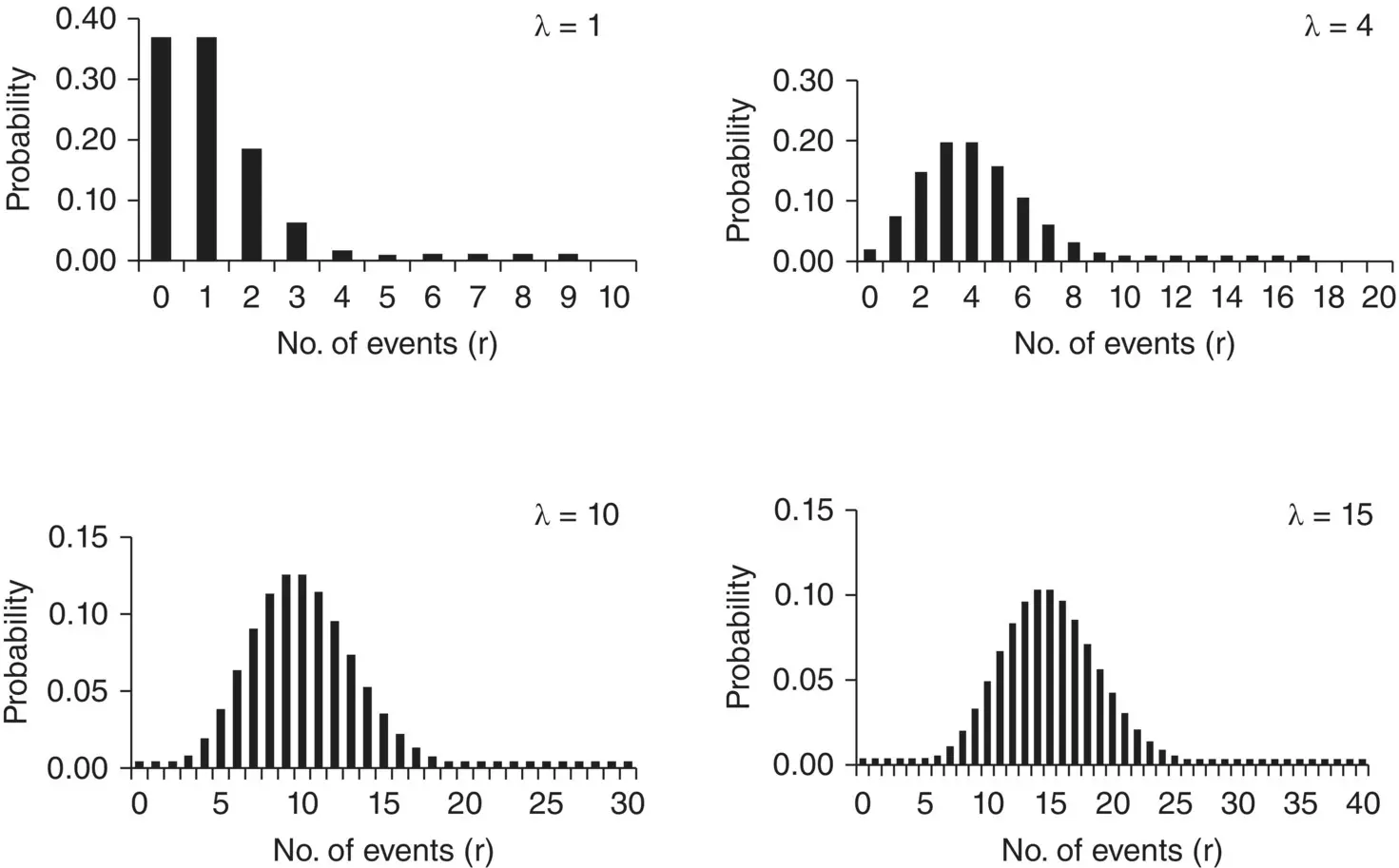
Figure 4.5 Poisson distribution for various values of λ. The horizontal scale in each diagram shows the value of r .
Example from the Literature – IV Treated Exacerbations in Patients with Cystic Fibrosis
CF is a genetic disorder that affects mostly the lungs. Long‐term issues include difficulty breathing and coughing up mucus as a result of frequent lung infections. There is no known cure for CF. Lung infections are treated with antibiotics which may be given intravenously (IV), inhaled, or by mouth. The build‐up of mucus in the lungs causes chronic infections, meaning that people with CF struggle with reduced lung function and have to spend hours doing physiotherapy and taking nebulised treatments each day. Exacerbations (a sudden worsening of health, often owing to infection) can lead to frequent hospitalisation for weeks at a time, interfering with work and home life.
Hind et al. (2019) looked at the incidence of IV treated exacerbations in patients with CF as part of a pilot randomised controlled trial (RCT). They observed 60 IV treated exacerbations in 60 patients with CF in six months of follow‐up (27 patients had no exacerbations; 14 had one; 13 had two, 4 had three and 2 patients had four). This gave a mean of one exacerbation per six months (see Figure 4.6). What is the probability of a patient having no exacerbations in a year assuming the data follow a Poisson distribution?
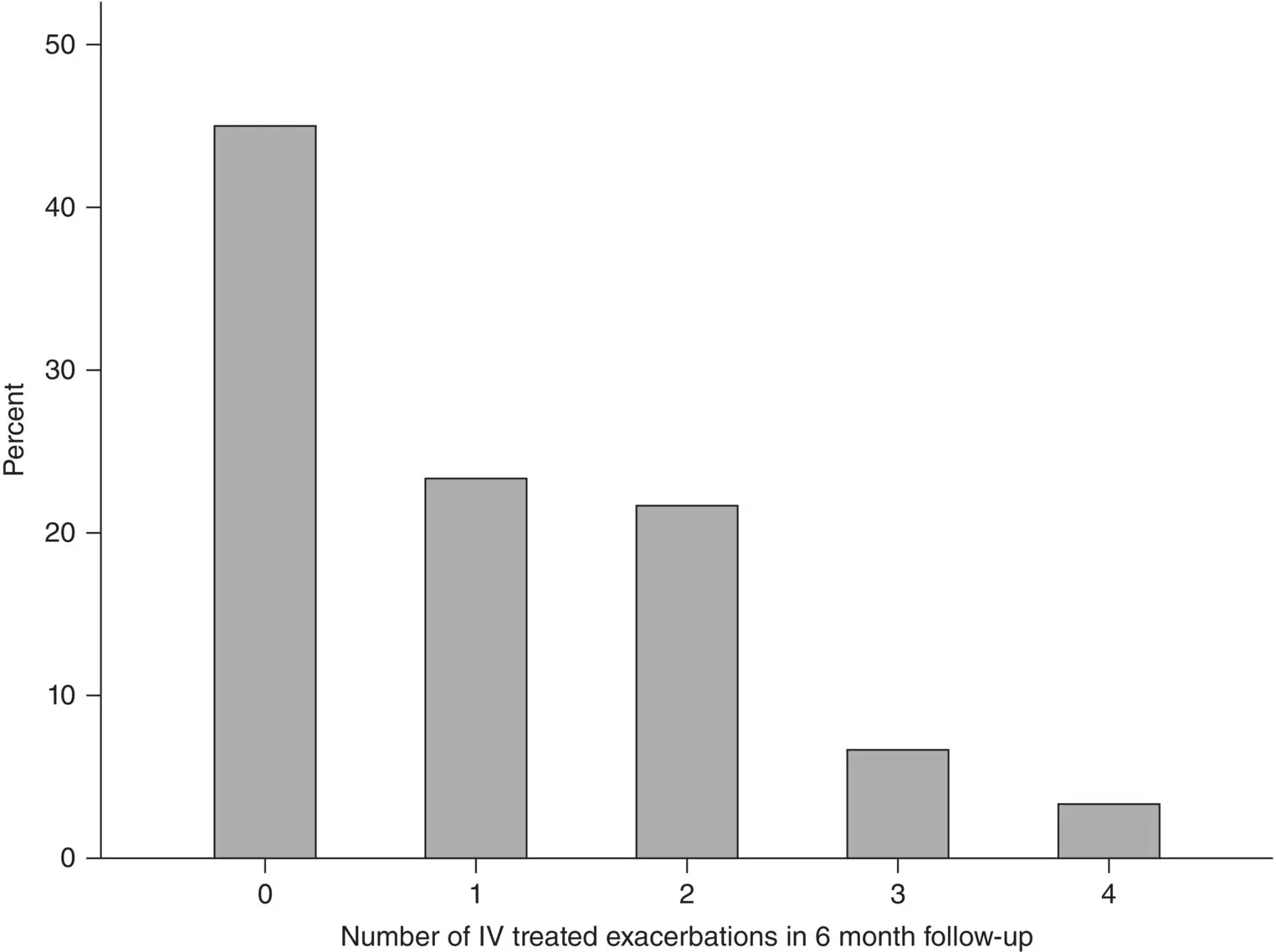
Figure 4.6 Relative frequency of IV treated exacerbations in 60 patients with cystic fibrosis over six months.
With this pilot RCT data would anticipate an average of λ = 1 × 2 = 2 exacerbations per year. Using this value in Eq. (4.2), for r = 0, 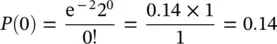 (since 0! = 1 and 2 0= 1). Thus there is about a 1 in 7 chance of a patient with CF not getting any exacerbations in any one year.
(since 0! = 1 and 2 0= 1). Thus there is about a 1 in 7 chance of a patient with CF not getting any exacerbations in any one year.
4.4 Probability for Continuous Outcomes
So far, we have looked at what is the probability of a particular value, for example, a success or failure on treatment. The Binomial and Poisson distributions are discrete distributions that describe discrete variables that can only take a limited set of values. As the number of possible values increases the probability of any particular value decreases. Continuous probability distributions are distributions that can take any value between given limits. For continuous variables, such as birth weight and blood pressure, the set of possible values is infinite (only limited by the precision of how were take the measurements). So, we are more interested in the probability of having values between certain limits rather than one particular value. For example, what is the probability of having a systolic blood pressure of 140 mmHg or higher?
The vertical scale of histograms, such as Figure 2.6, shown so far, have been frequencies and depend on the total number of observations. As an alternative we can use the relative frequency (or %) on the vertical scale. The advantage of using the relative frequency is that the scale of different histograms, with the same outcome but different sample sizes, will be the same. Such a histogram, as in Figure 4.7can be given the rather formal name of an empirical relative frequency distribution but it is simply the observed distribution of the data in a sample.
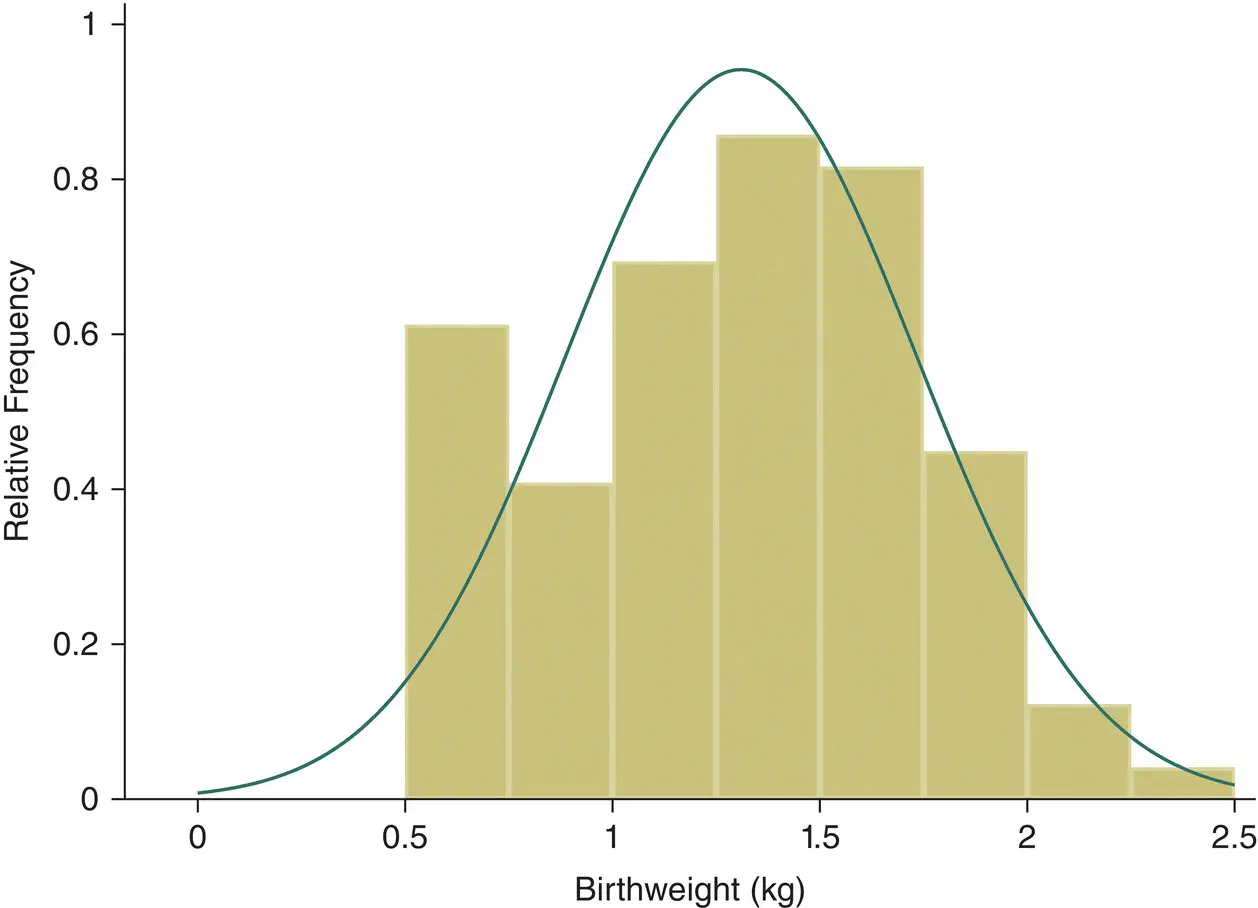
Figure 4.7 Empirical relative frequency distributions of birth weight of 98 babies admitted to special care baby unit and the associated probability distribution.
( Source: data from Simpson 2004). Reproduced by permission of AG Simpson.
If we imagine for the birthweight data in Figure 4.7that we have a very large sample (many more than 98 babies) and by taking smaller and smaller intervals to classify the birth weights (much smaller than 0.25 kg) then the histogram will start to look like a smooth curve (see Figure 4.8). In these circumstances the distribution of observations may be approximated by a smooth underlying curve, which is also shown in Figure 4.7. This curve is called a probability distribution and is the theoretical equivalent of an empirical relative frequency distribution. Probability distributions are used to calculate the probability that different values will occur, for example: what is the probability of having a birthweight of 2.0 kg or less? It is often the case with medical data that the histogram of a continuous variable obtained from a single measurement on different subjects will have a symmetric ‘bell‐shaped’ distribution.
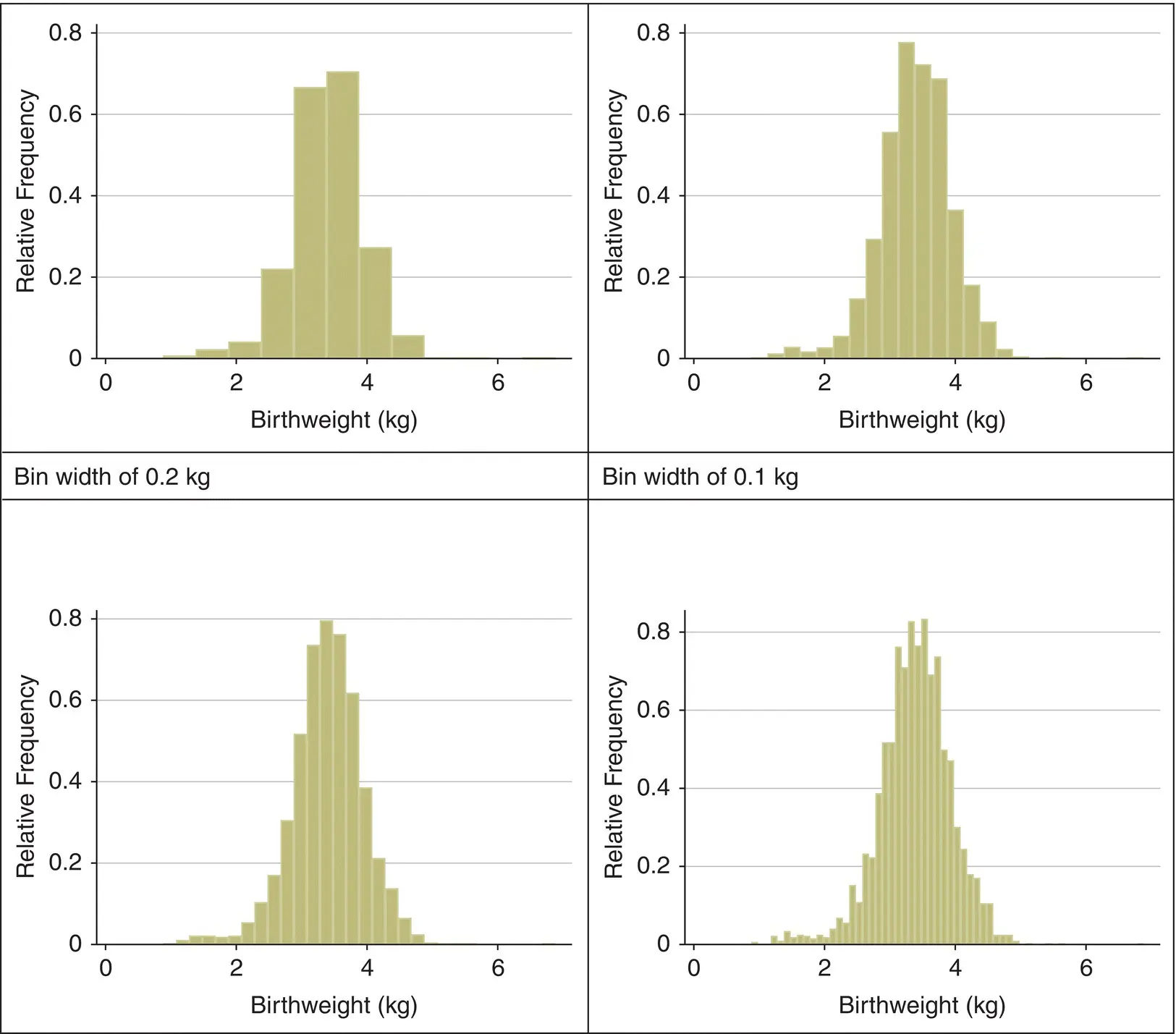
Figure 4.8 Empirical relative frequency distributions of birthweight with interval (bin) widths of 0.5, 0.25, 0.2, and 0.1 kg
Читать дальше



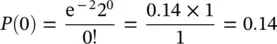 (since 0! = 1 and 2 0= 1). Thus there is about a 1 in 7 chance of a patient with CF not getting any exacerbations in any one year.
(since 0! = 1 and 2 0= 1). Thus there is about a 1 in 7 chance of a patient with CF not getting any exacerbations in any one year.












