The first was in digital cash ; you might want to be able to issue anonymous payment tokens to customers, and the earliest idea, due to David Chaum, was a way to sign ‘digital coins’ without knowing their serial numbers [413]. A bank might agree to honour for $10 any string 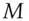 with a unique serial number and a specified form of redundancy, bearing a signature that verified as correct using the public key
with a unique serial number and a specified form of redundancy, bearing a signature that verified as correct using the public key 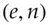 . The blind signature protocol ensures a customer can get a bank to sign a coin without the banker knowing its serial number, and it was used in prototype road toll systems. The effect is that the digital cash can be anonymous for the spender. The main problem with digital cash was to detect people who spend the same coin twice, and this was eventually fixed using blockchains or other ledger mechanisms, as I discuss in section 20.7. Digital cash failed to take off because neither banks nor governments really want payments to be anonymous: anti-money-laundering regulations since 9/11 restrict anonymous payment services to small amounts, while both banks and bitcoin miners like to collect transaction fees.
. The blind signature protocol ensures a customer can get a bank to sign a coin without the banker knowing its serial number, and it was used in prototype road toll systems. The effect is that the digital cash can be anonymous for the spender. The main problem with digital cash was to detect people who spend the same coin twice, and this was eventually fixed using blockchains or other ledger mechanisms, as I discuss in section 20.7. Digital cash failed to take off because neither banks nor governments really want payments to be anonymous: anti-money-laundering regulations since 9/11 restrict anonymous payment services to small amounts, while both banks and bitcoin miners like to collect transaction fees.
Anonymous digital credentials are now used in attestation: the TPM chip on your PC motherboard might prove something about the software running on your machine without identifying you. Unfortunately, this led to designs for attestation in SGX (and its AMD equivalent) which mean that a single compromised device breaks the whole ecosystem. Anonymous signatures are also found in prototype systems for conducting electronic elections, to which I will return in section 25.5.
5.7.8 How strong are asymmetric cryptographic primitives?
In order to provide the same level of protection as a symmetric block cipher, asymmetric cryptographic primitives generally require at least twice the block length. Elliptic curve systems appear to achieve this bound; a 256-bit elliptic scheme could be about as hard to break as a 128-bit block cipher with a 128-bit key; and the only public-key encryption schemes used in the NSA's Suite B of military algorithms are 384-bit elliptic curve systems. The traditional schemes, based on factoring and discrete log, now require 3072-bit keys to protect material at Top Secret, as there are shortcut attack algorithms such as the number field sieve. As a result, elliptic curve cryptosystems are faster.
When I wrote the first edition of this book in 2000, the number field sieve had been used to attack keys up to 512 bits, a task comparable in difficulty to keysearch on 56-bit DES keys; by the time I rewrote this chapter for the second edition in 2007, 64-bit symmetric keys had been brute-forced, and the 663-bit challenge number RSA-200 had been factored. By the third edition in 2019, bitcoin miners are finding 68-bit hash collisions every ten minutes, RSA-768 has been factored and Ed Snowden has as good as told us that the NSA can do discrete logs for a 1024-bit prime modulus.
There has been much research into quantum computers – devices that perform a large number of computations simultaneously using superposed quantum states. Peter Shor has shown that if a sufficiently large quantum computer could be built, then both factoring and discrete logarithm computations will become easy [1728]. So far only very small quantum devices have been built; although there are occasional claims of ‘quantum supremacy’ – of a quantum computer performing a task sufficiently faster than a conventional one to convince us that quantum superposition or entanglement is doing any real work – they seem to lead nowhere. I am sceptical (as are many physicists) about whether the technology will ever threaten real systems. I am even more sceptical about the value of quantum cryptography; it may be able to re-key a line encryption device that uses AES for bulk encryption on a single uninterrupted fibre run, but we already know how to do that.
What's more, I find the security proofs offered for entanglement-based quantum cryptography to be unconvincing. Theoretical physics has been stalled since the early 1970s when Gerard ’t Hooft completed the Standard Model by proving the renormalisability of Yang-Mills. Since then, a whole series of ideas have come and gone, such as string theory [2035]. Quantum information theory is the latest enthusiasm. Its proponents talk up the mystery of the Bell tests, which are supposed to demonstrate that physics cannot be simultaneously local and causal. But alternative interpretations such as ’t Hooft's cellular automaton model [918] and Grisha Volovik's superfluid model [1971] suggest that the Bell tests merely demonstrate the existence of long-range order in the quantum vacuum, like the order parameter of a superfluid. Since 2005, we've had lab experiments involving bouncing droplets on a vibrating fluid bath that demonstrate interesting analogues of quantum-mechanical properties relevant to the Bell tests [1560]. This book is not the place to discuss the implications in more detail; for that, see [312]. There is a whole community of physicists working on emergent quantum mechanics – the idea that to make progress beyond the Standard Model, and to reconcile the apparent conflict between quantum mechanics and general relativity, we may need to look at things differently. Meantime, if anyone claims their system is secure ‘because quantum mechanics’ then scepticism may be in order.
I think it more likely that a major challenge to public-key cryptography could come in the form of a better algorithm for computing discrete logarithms on elliptic curves. These curves have a lot of structure; they are studied intensively by some of the world's smartest pure mathematicians; better discrete-log algorithms for curves of small characteristic were discovered in 2013 [169]; and the NSA is apparently moving away from using elliptic-curve crypto.
If quantum computers ever work, we have other ‘post-quantum’ algorithms ready to go, for which quantum computers give no obvious advantage. In 2020, NIST began the third round of public review of submissions for the Post-Quantum Cryptography Standardization Process. The 65 initial submissions have been cut to 15 through two rounds of review 12. One or more algorithms will now be chosen and standardised, so ciphersuites using them could be dropped into protocols such as TLS as upgrades. Many protocols in use could even be redesigned to use variants on Kerberos. If elliptic logarithms become easy, we have these resources and can also fall back to discrete logs in prime fields, or to RSA. But if elliptic logs become easy, bitcoins will become trivial to forge, and the cryptocurrency ecosystem would probably collapse, putting an end to the immensely wasteful mining operations I describe in section 20.7. So mathematicians who care about the future of the planet might do worse than to study the elliptic logarithm problem.
5.7.9 What else goes wrong
Very few attacks on systems nowadays involve cryptanalysis in the sense of a mathematical attack on the encryption algorithm or key. There have indeed been attacks on systems designed in the 20th century, mostly involving keys that were kept too short by export-control rules, clueless designs or both. I already discussed in section 4.3.1how weak crypto has facilitated a wave of car theft, as all the devices used for remote key entry were defeated one after another in 2005–15. In later chapters, I give examples of how the crypto wars and their export control rules resulted in attacks on door locks ( section 13.2.5), mobile phones ( section 22.3.1) and copyright enforcement ( section 24.2.5).
Читать дальше

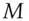 with a unique serial number and a specified form of redundancy, bearing a signature that verified as correct using the public key
with a unique serial number and a specified form of redundancy, bearing a signature that verified as correct using the public key 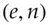 . The blind signature protocol ensures a customer can get a bank to sign a coin without the banker knowing its serial number, and it was used in prototype road toll systems. The effect is that the digital cash can be anonymous for the spender. The main problem with digital cash was to detect people who spend the same coin twice, and this was eventually fixed using blockchains or other ledger mechanisms, as I discuss in section 20.7. Digital cash failed to take off because neither banks nor governments really want payments to be anonymous: anti-money-laundering regulations since 9/11 restrict anonymous payment services to small amounts, while both banks and bitcoin miners like to collect transaction fees.
. The blind signature protocol ensures a customer can get a bank to sign a coin without the banker knowing its serial number, and it was used in prototype road toll systems. The effect is that the digital cash can be anonymous for the spender. The main problem with digital cash was to detect people who spend the same coin twice, and this was eventually fixed using blockchains or other ledger mechanisms, as I discuss in section 20.7. Digital cash failed to take off because neither banks nor governments really want payments to be anonymous: anti-money-laundering regulations since 9/11 restrict anonymous payment services to small amounts, while both banks and bitcoin miners like to collect transaction fees.









