The critical innovation, for the banks’ purposes, was to use a code book but to make the coding one-way by adding the code groups together into a number called a test key . (Modern cryptographers would describe it as a hash value or message authentication code , terms I'll define more carefully later.)
Here is a simple example. Suppose the bank has a code book with a table of numbers corresponding to payment amounts as in Figure 5.8.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| x 1000 |
14 |
22 |
40 |
87 |
69 |
93 |
71 |
35 |
06 |
58 |
| x 10,000 |
73 |
38 |
15 |
46 |
91 |
82 |
00 |
29 |
64 |
57 |
| x 100,000 |
95 |
70 |
09 |
54 |
82 |
63 |
21 |
47 |
36 |
18 |
| x 1,000,000 |
53 |
77 |
66 |
29 |
40 |
12 |
31 |
05 |
87 |
94 |
Figure 5.8 : A simple test key system
Now in order to authenticate a transaction for £376,514 we might add together 53 (no millions), 54 (300,000), 29 (70,000) and 71 (6,000) ignoring the less significant digits. This gives us a test key of 207.
Most real systems were more complex than this; they usually had tables for currency codes, dates and even recipient account numbers. In the better systems, the code groups were four digits long rather than two, and in order to make it harder for an attacker to reconstruct the tables, the test keys were compressed: a key of ‘7549’ might become ‘23’ by adding the first and second digits, and the third and fourth digits, ignoring the carry.
This made such test key systems into one-way functions in that although it was possible to compute a test from a message, given knowledge of the key, it was not possible to reverse the process and recover either a message or a key from a single test – the test just did not contain enough information. Indeed, one-way functions had been around since at least the seventeenth century. The scientist Robert Hooke published in 1678 the sorted anagram ‘ceiiinosssttuu’ and revealed two years later that it was derived from ‘Ut tensio sic uis’ – ‘the force varies as the tension’, or what we now call Hooke's law for a spring. (The goal was to establish priority for the idea while giving him time to do more work on it.)
Banking test keys are not strong by the standards of modern cryptography. Given between a few dozen and a few hundred tested messages, depending on the design details, a patient analyst could reconstruct enough of the tables to forge a transaction. With a few carefully chosen messages inserted into the banking system by an accomplice, it's even easier. But the banks got away with it: test keys worked fine from the late nineteenth century through the 1980s. In several years working as a bank security consultant, and listening to elderly auditors’ tales over lunch, I only ever heard of two cases of fraud that exploited it: one external attempt involving cryptanalysis, which failed because the attacker didn't understand bank procedures, and one successful but small fraud involving a crooked staff member. I'll discuss the systems that replaced test keys in the chapter on Banking and Bookkeeping.
However, test keys are our historical example of an algebraic function used for authentication. They have important modern descendants in the authentication codes used in the command and control of nuclear weapons, and also with modern block ciphers. The idea in each case is the same: if you can use a unique key to authenticate each message, simple algebra can give you ideal security. Suppose you have a message 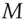 of arbitrary length and want to compute an authentication code or tag
of arbitrary length and want to compute an authentication code or tag 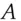 of 128 bits length, and the property you want is that nobody should be able to find a different message
of 128 bits length, and the property you want is that nobody should be able to find a different message 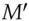 whose authentication code under the same key will also be
whose authentication code under the same key will also be 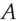 , unless they know the key, except by a lucky guess for which the probability is
, unless they know the key, except by a lucky guess for which the probability is 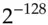 . You can simply choose a 128-bit prime number
. You can simply choose a 128-bit prime number 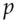 and compute
and compute 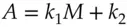 (mod
(mod 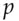 ) where the key consists of two 128-bit numbers
) where the key consists of two 128-bit numbers 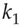 and
and 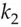 .
.
This is secure for the same reason the one-time pad is: given any other message 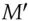 you can find another key
you can find another key  that authenticates
that authenticates 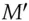 to
to 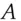 . So without knowledge of the key, the adversary who sees
. So without knowledge of the key, the adversary who sees 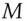 and
and 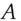 simply has no information of any use in creating a valid forgery. As there are 256 bits of key and only 128 bits of tag, this holds even for an adversary with unlimited computing power: such an adversary can find the
simply has no information of any use in creating a valid forgery. As there are 256 bits of key and only 128 bits of tag, this holds even for an adversary with unlimited computing power: such an adversary can find the 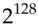 possible keys for each pair of message and tag but has no way to choose between them. I'll discuss how this universal hash function is used with block ciphers below, and how it's used in nuclear command and control in Part 2.
possible keys for each pair of message and tag but has no way to choose between them. I'll discuss how this universal hash function is used with block ciphers below, and how it's used in nuclear command and control in Part 2.
5.2.5 Asymmetric primitives
Finally, some modern cryptosystems are asymmetric, in that different keys are used for encryption and decryption. So, for example, most web sites nowadays have a certificate containing a public key with which people can encrypt their session using a protocol called TLS; the owner of the web page can decrypt the traffic using the corresponding private key . We'll go into the details later.
There are some pre-computer examples of this too; perhaps the best is the postal service. You can send me a private message by addressing it to me and dropping it into a post box. Once that's done, I'm the only person who'll be able to read it. Of course, many things can go wrong: you might get the wrong address for me (whether by error or as a result of deception); the police might get a warrant to open my mail; the letter might be stolen by a dishonest postman; a fraudster might redirect my mail without my knowledge; or a thief might steal the letter from my doormat. Similar things can go wrong with public key cryptography: false public keys can be inserted into the system, computers can be hacked, people can be coerced and so on. We'll look at these problems in more detail in later chapters.
Читать дальше

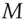 of arbitrary length and want to compute an authentication code or tag
of arbitrary length and want to compute an authentication code or tag 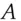 of 128 bits length, and the property you want is that nobody should be able to find a different message
of 128 bits length, and the property you want is that nobody should be able to find a different message 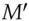 whose authentication code under the same key will also be
whose authentication code under the same key will also be 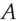 , unless they know the key, except by a lucky guess for which the probability is
, unless they know the key, except by a lucky guess for which the probability is 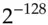 . You can simply choose a 128-bit prime number
. You can simply choose a 128-bit prime number 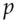 and compute
and compute 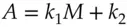 (mod
(mod 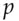 ) where the key consists of two 128-bit numbers
) where the key consists of two 128-bit numbers 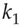 and
and 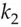 .
.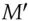 you can find another key
you can find another key  that authenticates
that authenticates 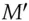 to
to 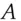 . So without knowledge of the key, the adversary who sees
. So without knowledge of the key, the adversary who sees 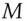 and
and 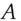 simply has no information of any use in creating a valid forgery. As there are 256 bits of key and only 128 bits of tag, this holds even for an adversary with unlimited computing power: such an adversary can find the
simply has no information of any use in creating a valid forgery. As there are 256 bits of key and only 128 bits of tag, this holds even for an adversary with unlimited computing power: such an adversary can find the 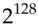 possible keys for each pair of message and tag but has no way to choose between them. I'll discuss how this universal hash function is used with block ciphers below, and how it's used in nuclear command and control in Part 2.
possible keys for each pair of message and tag but has no way to choose between them. I'll discuss how this universal hash function is used with block ciphers below, and how it's used in nuclear command and control in Part 2.









