The Arabs generalised this idea to the monoalphabetic substitution , in which a keyword is used to permute the cipher alphabet. We will write the plaintext in lower case letters, and the ciphertext in upper case, as shown in Figure 5.1:
abcdefghijklmnopqrstuvwxyz SECURITYABDFGHJKLMNOPQVWXZ
Figure 5.1 : Monoalphabetic substitution cipher
OYAN RWSGKFR AN AH RHTFANY MSOYRM OYSH SMSEAC NCMAKO; but it's a pencil and paper puzzle to break ciphers of this kind. The trick is that some letters, and combinations of letters, are much more common than others; in English the most common letters are e,t,a,i,o,n,s,h,r,d,l,u in that order. Artificial intelligence researchers have experimented with programs to solve monoalphabetic substitutions. Using letter and digram (letter pair) frequencies alone, they typically need about 600 letters of ciphertext; smarter strategies such as guessing probable words can cut this to about 150 letters; and state-of-the-art systems that use neural networks and approach the competence of human analysts are also tested on deciphering ancient scripts such as Ugaritic and Linear B [1196].
There are basically two ways to make a stronger cipher – the stream cipher and the block cipher . In the former, you make the encryption rule depend on a plaintext symbol's position in the stream of plaintext symbols, while in the latter you encrypt several plaintext symbols at once in a block.
5.2.1 An early stream cipher – the Vigenère
This early stream cipher is commonly ascribed to the Frenchman Blaise de Vigenère, a diplomat who served King Charles IX. It works by adding a key repeatedly into the plaintext using the convention that ‘A’ = 0, ‘B’ = 1, …, ‘Z’ = 25, and addition is carried out modulo 26 – that is, if the result is greater than 25, we subtract as many multiples of 26 as are needed to bring it into the range [0, …, 25], that is, [A, …, Z]. Mathematicians write this as
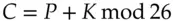
So, for example, when we add P (15) to U (20) we get 35, which we reduce to 9 by subtracting 26. 9 corresponds to J, so the encryption of P under the key U (and of U under the key P) is J, or more simply U + P = J. In this notation, Julius Caesar's system used a fixed key 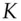 = D, while Augustus Caesar's used
= D, while Augustus Caesar's used 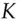 = C and Vigenère used a repeating key, also known as a running key . Techniques were developed to do this quickly, ranging from printed tables to brass cipher wheels. Whatever the technology, the encryption using a repeated keyword for the key would look as shown in Figure 5.2:
= C and Vigenère used a repeating key, also known as a running key . Techniques were developed to do this quickly, ranging from printed tables to brass cipher wheels. Whatever the technology, the encryption using a repeated keyword for the key would look as shown in Figure 5.2:
| Plain |
tobeornottobethatisthequestion |
| Key |
runrunrunrunrunrunrunrunrunrun |
| Cipher |
KIOVIEEIGKIOVNURNVJNUVKHVMGZIA |
Figure 5.2 : Vigenère (polyalphabetic substitution cipher)
A number of people appear to have worked out how to solve polyalphabetic ciphers, from the womaniser Giacomo Casanova to the computing pioneer Charles Babbage. But the first published solution was in 1863 by Friedrich Kasiski, a Prussian infantry officer [1023]. He noticed that given a long enough piece of ciphertext, repeated patterns will appear at multiples of the keyword length.
In Figure 5.2, for example, we see ‘ KIOV’ repeated after nine letters, and ‘ NU’ after six. Since three divides both six and nine, we might guess a keyword of three letters. Then ciphertext letters one, four, seven and so on were all enciphered under the same keyletter; so we can use frequency analysis techniques to guess the most likely values of this letter, and then repeat the process for the remaining letters of the key.
One way to make a stream cipher of this type proof against attacks is for the key sequence to be as long as the plaintext, and to never repeat. This is known as the one-time pad and was proposed by Gilbert Vernam during World War I [1003]; given any ciphertext, and any plaintext of the same length, there's a key that decrypts the ciphertext to the plaintext. So regardless of the amount of computation opponents can do, they're none the wiser, as given any ciphertext, all possible plaintexts of that length are equally likely. This system therefore has perfect secrecy .
Here's an example. Suppose you had intercepted a message from a wartime German agent which you knew started with ‘Heil Hitler’, and the first ten letters of ciphertext were DGTYI BWPJA. So the first ten letters of the one-time pad were wclnb tdefj, as shown in Figure 5.3:
| Plain |
heilhitler |
| Key |
wclnbtdefj |
| Cipher |
DGTYIBWPJA |
Figure 5.3 : A spy's message
But once he's burnt the piece of silk with his key material, the spy can claim that he's actually a member of the underground resistance, and the message actually said ‘Hang Hitler’. This is also possible, as the key material could just as easily have been wggsb tdefj, as shown in Figure 5.4:
| Cipher |
DGTYIBWPJA |
| Key |
wggsbtdefj |
| Plain |
hanghitler |
Figure 5.4 : What the spy can claim he said
Now we rarely get anything for nothing in cryptology, and the price of the perfect secrecy of the one-time pad is that it fails completely to protect message integrity. So if you wanted to get this spy into trouble, you could change the ciphertext to DCYTI BWPJA( Figure 5.5):
| Cipher |
DCYTIBWPJA |
| Key |
wclnbtdefj |
| Plain |
hanghitler |
Figure 5.5 : Manipulating the message to entrap the spy
Leo Marks’ engaging book on cryptography in the Special Operations Executive in World War II [1226] relates how one-time key material was printed on silk, which agents could conceal inside their clothing; whenever a key had been used it was torn off and burnt. In fact, during the war, Claude Shannon proved that a cipher has perfect secrecy if and only if there are as many possible keys as possible plaintexts, and every key is equally likely; so the one-time pad is the only kind of system that offers perfect secrecy. He was finally allowed to publish this in 1948 [1717, 1718].
The one-time tape was used for top-level communications by both sides from late in World War II, then for strategic communications between NATO allies, and for the US-USSR hotline from 1963. Thousands of machines were produced in total, using paper tapes for key material, until they were eventually replaced by computers from the mid-1980s 1. But such cryptography is too expensive for most applications as it consumes as much key material as there is traffic. It's more common for stream ciphers to use a pseudorandom number generator to expand a short key into a long keystream. The data is then encrypted by combining the keystream, one symbol at a time, with the data. It's not enough for the keystream to appear “random” in the sense of passing the standard statistical randomness tests: it must also have the property that an opponent who gets his hands on even quite a lot of keystream symbols should not be able to predict any more of them.
Читать дальше

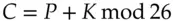
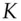 = D, while Augustus Caesar's used
= D, while Augustus Caesar's used 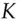 = C and Vigenère used a repeating key, also known as a running key . Techniques were developed to do this quickly, ranging from printed tables to brass cipher wheels. Whatever the technology, the encryption using a repeated keyword for the key would look as shown in Figure 5.2:
= C and Vigenère used a repeating key, also known as a running key . Techniques were developed to do this quickly, ranging from printed tables to brass cipher wheels. Whatever the technology, the encryption using a repeated keyword for the key would look as shown in Figure 5.2:









