Position, Navigation, and Timing Technologies in the 21st Century

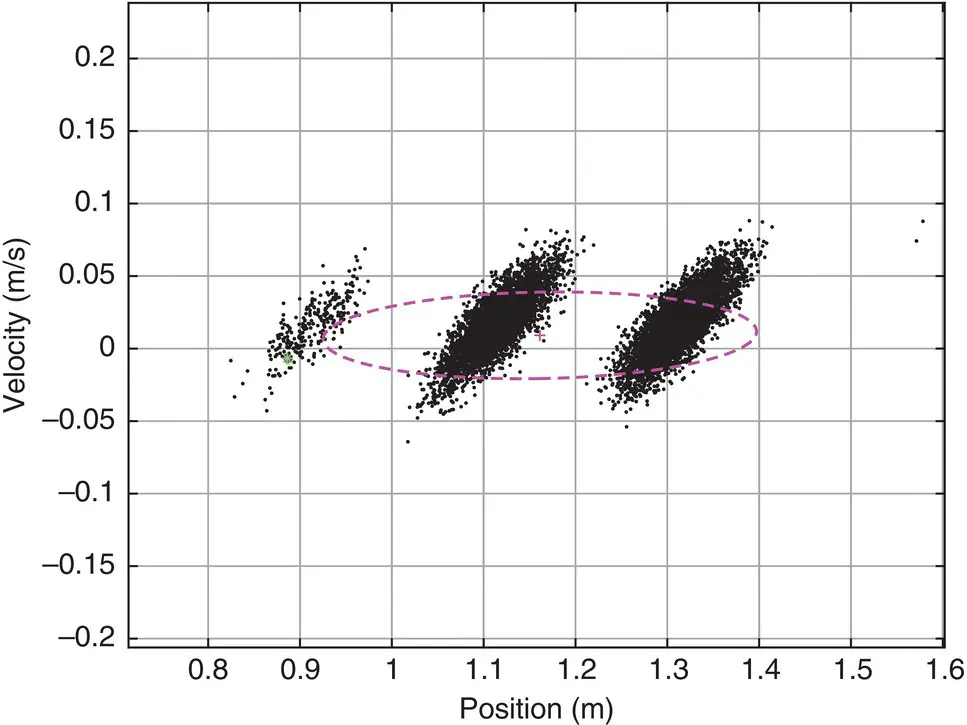
Figure 36.18 SIR particle filter state estimate (after 22 observations). Range observations combined with the vehicle dynamics model are eliminating unlikely integer ambiguity values.

The global state estimate and associated standard deviation result for this simulation is shown in Figure 36.20. The shape of the uncertainty bound clearly shows the effects described above. As the likelihood of each integer ambiguity realization changes, the overall uncertainty changes and eventually collapses to the centimeter level.

In this chapter, we have presented three classes of nonlinear recursive estimation algorithms. While each algorithm offers improved performance over the linear and extended Kalman filter in the presence of nonlinearities and non‐Gaussian systems, it is important to address the “strengths and weaknesses” of each. To accomplish this, we evaluate each estimation from this perspective, starting with the traditional approaches.

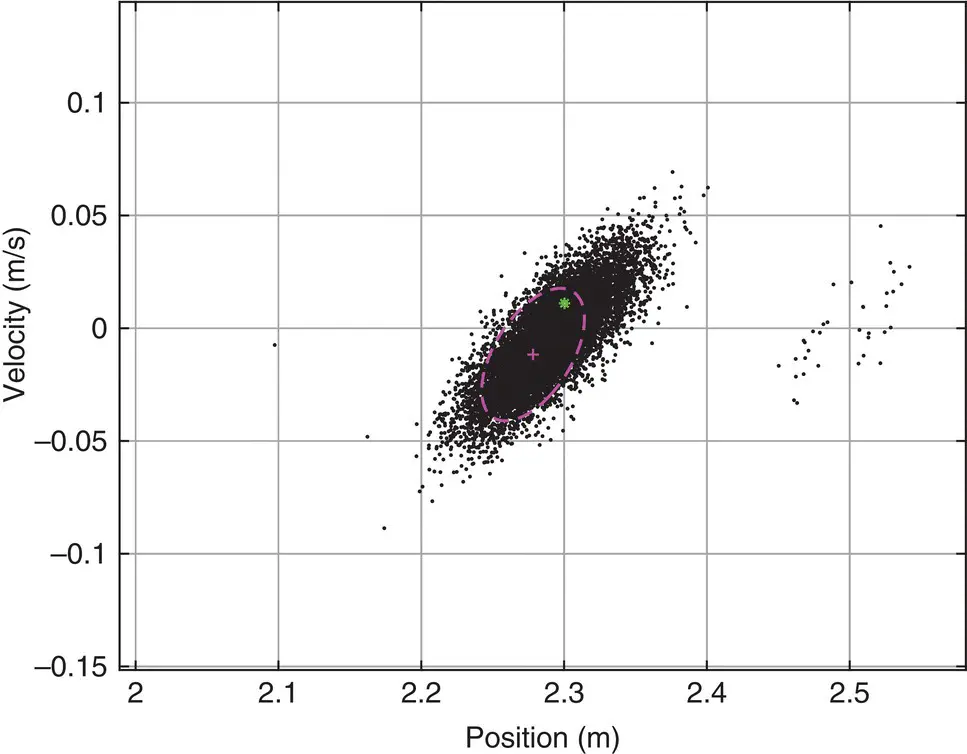
Figure 36.19 SIR particle filter state estimate (after 100 observations). Note that the state estimate is almost completely unimodal and has converged to the correct integer ambiguity.

Figure 36.20 SIR particle filter position error and one‐sigma uncertainty. Note that the error uncertainty collapses once sufficient information is available to resolve the integer ambiguity.

As expected, each approach has a set of associated strengths and weaknesses that can greatly influence the results for a given problem. Thus, the choice of estimator must be considered carefully based on the characteristics of the problem at hand. In cases where the constraints of the problem do not readily fit into the generalized categories above, there are many examples of hybrid estimation schemes that seek to synergistically combine the desirable properties of multiple estimator types. While it is beyond the scope of this chapter to explore the range of hybrid filtering approaches, the interested reader is referred to the references (e.g. [4, 5, 6, 9, 10]) for foundational concepts.

In this chapter, we have presented an overview of nonlinear estimation approaches suitable for navigation problems. Starting with first principles, three classes of nonlinear, recursive estimators were derived, the performance was demonstrated using a common navigation example application, and comparisons were made between the approaches.

The growing availability of a wide range of sensors and improved computational resources has heralded a new era of multisensor navigation. Because many of these sensors have nonlinear and non‐Gaussian error models, researchers are developing a range of recursive navigation algorithms to meet these requirements.

When used within their associated limitations, nonlinear estimation algorithms hold enormous promise for addressing the most difficult navigation problems.

1 1 Kalman, R.E. (1960) A new approach to linear filtering and prediction problems. Transactions of the ASME–Journal of Basic Engineering, 82 (Series D), 35–45.

2 2 Maybeck, P.S. (1979) Stochastic Models, Estimation, and Control, Vol. I, Academic Press, Inc., Orlando, Florida 32887.

3 3 Maybeck, P.S. (1979) Stochastic Models, Estimation, and Control, Vol II, Academic Press, Inc., Orlando, Florida 32887.

4 4 Gordon, N.J., Salmond, D.J., and Smith, A.F. (1993) Novel approach to nonlinear/non‐Gaussian Bayesian state estimation, in IEE Proceedings F‐Radar and Signal Processing, vol. 140, IET, vol. 140, pp. 107–113.

5 5 Doucet, A., De Freitas, N., and Gordon, N. (2001) Sequential Monte Carlo Methods in Practice. Series Statistics for Engineering and Information Science.

6 6 Ristic, B., Arulampalam, S., and Gordon, N. (2004) Beyond the Kalman Filter: Particle Filters for Tracking Applications, Artech House.

7 7 Sheldon, S. and Maybeck, P. (1990) An optimizing design strategy for multiple model adaptive estimation and control, in Decision and Control, 1990, Proceedings of the 29th IEEE Conference on, pp. 3522–3527, Vol. 6.

8 8 Bar‐Shalom, Y., Li, X.R., and Kirubarajan, T. (2004) Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software, John Wiley & Sons.

9 9 Doucet, A., de Freitas, N., Murphy, K., and Russell, S. (2000) Rao‐Blackwellised particle filtering for dynamic Bayesian networks, in Proceedings of the Sixteenth Conference on Uncertainty in Artificial Intelligence, Morgan Kaufmann Publishers Inc., San Francisco, California, UAI’00, pp. 176–183. URL http://dl.acm.org/citation.cfm?id=2073946.2073968.

10 10 Mustiere, F., Bolic, M., and Bouchard, M. (2006) Rao‐Blackwellised particle filters: Examples of applications, in Electrical and Computer Engineering, 2006. CCECE ‘06. Canadian Conference on, pp. 1196–1200.

11 11 Papoulis, A. and Pillai, S.U. (2002) Probability, Random Variables and Stochastic Processes, McGraw‐Hill, New York.

Sudeep Pasricha

Colorado State University, United States

While localization and navigation in outdoor environments can make use of global navigation satellite systems (GNSSs) such as Global Positioning System (GPS), this is not a viable solution for indoor localization because signals from GPS satellites are too weak to penetrate through buildings, obstacles, and into underground environments. Consequently, precise localization inside a closed structure, such as shopping malls, hospitals, airports, subways, and university campus buildings, require the use of alternative localization technologies. But indoor environments present unique challenges, particularly due to a diverse array of obstacles such as walls, doors, furniture, electronic equipment, and stationary or moving humans, all of which give rise to multipath effects in wireless signals due to signal reflection, attenuation, and noise interference. As a result, accurate indoor localization with wireless communication signals is a very complex problem. Moreover, indoor locales also require much higher levels of accuracy than outdoor environments; for example, while a 4–6 m accuracy is acceptable outdoors for vehicle navigation, it may not be acceptable for localization in many indoor contexts, where 4–6 m may be the difference between one room and the next.

Enabling location services for indoor locales has many potential applications. Buildings with awareness of the location of occupants can use this knowledge to optimize heating, lighting, and other resources toward saving energy costs. In emergency scenarios such as earthquakes and hurricanes, location services can allow emergency responders to determine where people are located at any time, potentially expediting evacuations as well as search and rescue efforts. Location awareness can be used as a backbone for smarter workplaces by allowing telephone calls to be routed to the nearest device in the proximity of a person, allowing colleagues to find each other, and helping guests navigate new buildings to reach their desired location. Services that utilize indoor location systems can also enable smart dynamic locking of sensitive rooms and resources if an owner is not present, to improve overall safety. Ubiquitous localization already plays a central role in social networking, for instance, to locate friends for coordinating joint activities or check into restaurants and other indoor locales via various smartphone apps, and is expected to play an even bigger role in the future. Indoor position awareness is also an essential component of industrial applications, such as for robot motion guidance, robot cooperation, and smart factories (e.g. the ability to find tagged maintenance tools and equipment scattered all over a plant in production facilities). Localization for cargo management systems at airports, ports, and for rail traffic enables unprecedented opportunities for increasing their efficiency.