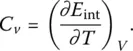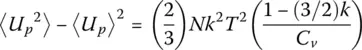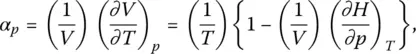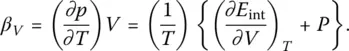Encyclopedia of Glass Science, Technology, History, and Culture

and the molar heat capacity at constant volume ( C v):

(26)

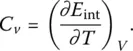
Alternatively, one can derive C vfrom the potential energy fluctuations through

(27)

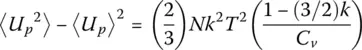
and two other interesting properties are the thermal expansion coefficient, ( α p)

(28)

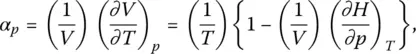
where H is enthalpy, and the thermal pressure coefficient ( β V):

(29)

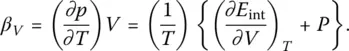
After a model of atomistic simulation is validated so that it can reproduce static structure of glass, it can be applied to investigate transport and dynamical properties such as diffusion constants, viscosity, or the Van Hove correlation function ( Chapter 4.6).

The statically arrangement of structural units for B 2O 3glass and the dynamically arrangement of structural units for SiO 2glass represent new insights on glass structure provided by MD simulations, in these cases, by the TAD, which escape any experimental determinations. These two examples thus illustrate the complementary nature of numerical simulations and experimental studies of glass structure. When the history of structural studies on glass is looked back on, it is clear that both diffraction and spectroscopic studies have made fundamental contributions to the construction of structural models. The RDF or the PDF can indeed be readily calculated from the Fourier transform of experimental X‐ray, neutron, or electron diffraction data ( Chapter 2.2). Because this type of information represents averaged one‐dimensional structural data, however, there is always some arbitrariness when reconstructing the actual three‐dimensional configuration in which one is interested.

Other probes such as IR, Raman, or NMR spectroscopies can provide information only on short‐range order in glass structure. In contrast, atomistic simulations do provide realistic three‐dimensional configuration directly as long as an appropriate atomistic model is employed. One could confidently argue that a structural model of glass is reliable when the model matches the results of both experiments and atomistic simulations. In summary, the relation between atomistic simulation and experiment is complementary because both methodologies provide insights on different aspects of glass structure. Atomistic simulations nonetheless possess two other advantages over experimental methods. The first is that they can determine three‐dimensional configurations from short‐ to medium‐range order extending up to the size of cell length (10–100 nm). The second is that a very broad range of atomistic simulations become possible as soon as an appropriate simulation model is established. For example, it is easy to change external conditions such as temperature, pressure, or other external forces to investigate their effects on structure. And physical and chemical properties can be readily derived from the potential‐energy and structural models with standard statistical mechanical methods.

Development of both faster computing processors and efficient simulation algorithms have expanded the range of atomistic simulations and narrowed down their discrepancies with experiments. Simulations would nonetheless benefit from improved accuracy. As becoming more common, the best way to achieve this goal is to perform first‐principles MD calculation from beginning to end. Although such calculations made with standard quantum mechanical codes remain difficult when dealing with a large number of atoms, progress should result from the use of the so‐called order‐ N and linear scaling methods, which have developed vigorously during the past decade. For oxide glasses, recent codes such as SIESTA or CONQUEST now have the potential ability to handle systems of around one thousand atoms with a supercomputer whereas calculations for systems ten times bigger should become feasible in the next decade. Alternatively, better classical potentials can be derived from the energy data yielded by ab‐initio methods as well illustrated by the Tuneyuki and BKS potentials used for silica glass that were based on the simple Buckingham function [4]. Whereas parameter fitting of these potential models was handmade, automatic fitting by machine learning methods is becoming popular since a huge number of data can be sampled on potential energy surfaces yielded by first‐principles calculations to derive better interatomic potentials. And even if the simulation remains based on classical mechanics, the shell, polarizable, charge‐equilibrium, and other models will be more widely used to reproduce better structures and properties [4].

The two other main limitations of numerical simulations currently concern the space‐ and timescales considered. To cope with them, combinations of two different techniques may be used as already described in Section 3for RMC methods. Besides, MC algorithms can be integrated into MD calculations to speed up simulation of too slow structural relaxation as is the case for the formation of boroxol rings in B 2O 3[11]. Of more general use, however, is a combination of classical and first‐principles MD simulations [20] whereby the former yield a preliminary structure that is subsequently optimized in the latter before spectroscopic or other properties are finally derived from the first‐principles simulations.

The “coarse‐graining” methods are also promising as multi‐scale simulation procedures. By lumping groups of atoms into larger entities referred to as particles, which interact according to newly parametrized effective interaction potentials, they have been successfully used for polymers to describe slow dynamic modes and to investigate the cooperative motions and fluctuations observed in the intermediate‐ and long‐range regions. For oxide glasses, however, their application is hampered by the difficulty of assigning appropriate structural fragments to coarse‐grained units.

Finally, it is important for glass scientists to share their know‐how on simulation techniques and interatomic potentials. One of such activities takes place in the TC‐3 Technical committee of the International Commission on Glass (ICG) where round‐robin tests are made to compare experimental data and calculated results on standard glass samples. Such an activity will provide useful information to other glass scientists on agreement and discrepancy between experiments and atomic simulations. Another activity is conducted in TC‐27 whose members discuss future directions of atomistic simulations, promote standardization of atomistic techniques, and provide information on these techniques to the glass community (e.g. [21]). In addition, ICG has published an educational textbook, which includes one chapter on atomistic simulations [22].

In a near future, we strongly expect that any macroscopic property will be explained in terms of microscopic structure by atomistic and first‐principles simulations. In addition, computational design of glass materials will advance rapidly in good harmony with experimental studies.