Jordi Juvé Udina - Preparación de productos específicos para acabados decorativos. MAMR0208

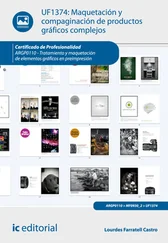
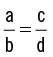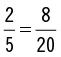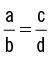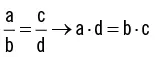Ahora a y b son dos magnitudes mensurables que se pretenden relacionar con otras dos, c y d. La interpretación de esta proporción es la que sigue: a es a b como c es a d.

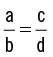
Los valores de a, b, c y d anteriores forman una proporción entre sí, en la que la razón entre a y b es la misma que entre c y d y, por tanto, en la siguiente proporción se cumple que: 2 es a 5 como 8 es a 20.

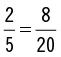
Las razones serán exactamente las mismas (0,40). Efectivamente, el resultado del cociente recibe el nombre de constante de proporcionalidad y tiene una gran importancia en la resolución de problemas que tratan de repartos proporcionales.

En una proporción, los componentes tienen sus propias denominaciones. Así, en una proporción de dos razones, en donde hay cuatro términos, se llaman componentes extremos de la proporción a los valores correspondientes al numerador de la primera razón y al denominador de la segunda y se llaman componentes medios de la proporción a los valores correspondientes al denominador de la primera razón y al numerador de la segunda.

A a y d se les denomina extremos, mientras que a b y c se les llama medios.

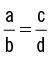
Una de las propiedades fundamentales de las proporciones es que el producto de los extremos es igual al de los medios.

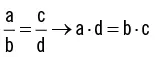
Dada la propiedad fundamental anterior, es posible calcular cualquier término de una proporción cuando se conocen los otros tres. A este elemento desconocido se le denomina cuarta proporcional y se representa con la letra x.

Efectivamente, un caso particular de las proporciones, compuestas de dos razones, en la que se desconoce uno de los términos de una de las razones, es la denominada regla de tres simple directa. Este es un procedimiento de resolución de problemas de proporcionalidad muy útil para calcular el valor de una cantidad (incógnita) comparándola con otros tres valores conocidos ya que, por lo visto anteriormente, se establece una relación de proporcionalidad entre los valores por la propiedad de que el producto de los extremos es igual al de los medios.

Nota

Cualquier regla de tres presenta una hipótesis y una incógnita. La hipótesis son los datos planteados en un problema y que se conocen, mientras que la incógnita es el resultado que se busca y se desea conocer.

Conocidos los valores de las magnitudes a, b y c, se desea conocer la incógnita d, que pasa a denominarse x.

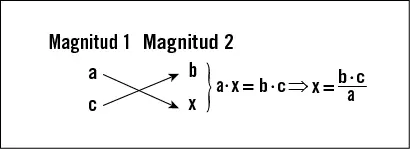
Otro caso particular de las proporciones, cuando las fracciones se emplean como razones, son los porcentajes (tanto por ciento), en los que la relación de proporcionalidad se establece entre un número y el número cien. El uso de porcentajes es un método universal que permite comparar fácilmente unas proporciones con otras y constituye uno de los lenguajes matemáticos de uso más extendido en la vida cotidiana, siendo muy frecuente su empleo para indicar cuánto representa una cantidad respecto a otra.

Un porcentaje expresa una proporción o cantidad relativa en la que el denominador es el número cien y su expresión es del tipo a% (de b), donde a es una parte de una cantidad absoluta denominada cantidad de referencia (b). Por tanto a% equivale a la fracción a/100, con lo cual es muy usual ver los porcentajes expresados con el símbolo %, pero también como fracción a/100 o como número decimal.

100% = 100/100 = 1

50% = 50/100 = 0,5

La empresa Barnizados EIS se dedica a dar acabado a hojas de puerta lisa que produce una fábrica próxima de puertas-block y con ello tiene un consumo anual total de 5.000 litros de productos de acabado. Básicamente, para el acabado de las superficies consume tintes NGR de coloraciones diversas para el tintado de las puertas y barniz hidrosoluble a base de dos componentes, en una proporción de 2:3.

La mezcla de barniz hidrosoluble a base de dos componentes se realiza con una adición de catalizador sobre el barniz base con una proporción de 1:2. Esta mezcla, posteriormente, se diluye en un 15%.

En primer lugar, se debe calcular las cantidades absolutas en litros correspondientes a tinte NGR y a barniz hidrosoluble en función de la proporción dada de 2:3, es decir, de los 5.000 litros de productos de acabado consumidos anualmente, 2 partes son de tintes NGR y 3 partes de barniz hidrosoluble.

La suma total de las partes es:

2 partes + 3 partes = 5 partes

Las razones de proporcionalidad serán:

2 partes / 5 partes = x litros / 5.000 litros

o

2/5 = x / 5.000

Despejando,

x = 2 ∙ 5.000 / 5

x = 2.000 litros de tintes NGR

Análogamente, se calcula la cantidad absoluta de barniz hidrosoluble:

x = 3.000 litros de barniz hidrosoluble preparado

El barniz hidrosoluble está formado por dos componentes: el barniz base y el reactivo o catalizador en una proporción de 1:2. En estos 3.000 litros de barniz hidrosoluble formado por dos componentes se ha mezclado, para poderlo aplicar correctamente, un 15% de diluyente (agua). Por lo que habrá que calcular la cantidad absoluta de cada uno de los componentes: barniz base, catalizador y diluyente.

Se calcula, en primer lugar, la cantidad de diluyente. En este caso, se busca una cantidad de barniz hidrosoluble formado por dos componentes de valor desconocido (incógnita) en el que, añadiéndole un 15% de diluyente, se obtengan los 3.000 litros consumidos anualmente:

x + 15% ∙ x = 3.000 litros

Es muy usual ver los porcentajes expresados con el símbolo %, pero también como fracción a/100 o como número decimal. Por tanto, para poder operar, se realiza la operación:

15% = 15/100 = 0,15

Por lo que la ecuación anterior será equivalente a:

x + 15% ∙ x = 3.000 litros

x + 0,15 ∙ x = 3.000 litros

x + 0,15x = 3.000 litros

1,15x = 3.000 litros

x = 3.000 litros / 1,15

x = 2608,7 litros de barniz hidrosoluble formado por dos componentes

Por lo que la cantidad de diluyente será:

3.000 litros de barniz hidrosoluble preparado -

- 2608,7 litros de barniz hidrosoluble formado por dos componentes =

= 391,3 litros de diluyente

Se calcula a continuación la cantidad de cada uno de los componentes básicos del barniz hidrosoluble. De los 2608,7 litros de barniz hidrosoluble formado por dos componentes, 1 parte corresponde al catalizador y 2 partes al barniz base. La suma total de las partes es:

1 partes + 2 partes = 3 partes

Las razones de proporcionalidad serán:

1 parte / 3 partes = x litros / 2608,7 litros

o

1 / 3 = x / 2608,7

Despejando,

x = 1 ∙ 2608,7 / 3

x = 869,6 litros de catalizador

Análogamente, se calcula la cantidad absoluta de barniz base:

x = 1739,1 litros de barniz base