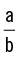Jordi Juvé Udina - Preparación de productos específicos para acabados decorativos. MAMR0208

Las implicaciones y responsabilidades: competencias de los procesos descritos en cuanto a las responsabilidades y la autoridad en la ejecución y registro.

Las referencias: normas y documentos diversos relacionados con la instrucción.

La terminología: definiciones aclaratorias, acrónimos o siglas, y términos relativos al contenido de la instrucción.

La descripción: desarrollo de los procesos objeto de la instrucción, con especial énfasis en la metodología y los registros derivados de la ejecución.

Los anexos: representaciones gráficas a modo de diagramas, cuadros, croquis, etcétera, para un correcto desarrollo de la instrucción.

El cuadro de ediciones: número de edición, fecha de aprobación, vigencia, modificaciones y sus causas.

La aprobación: nombre, cargo, fecha y firma de las personas responsables de la elaboración, revisión y aprobación de la instrucción.

Las magnitudes físicas más importantes de los productos de acabado de la madera tienen relación directa con la medida y, por tanto, ofrecen la posibilidad de comparación de un objeto con otro de la misma naturaleza que se toma como referencia. Por ende, será necesaria la determinación de la dimensión de una magnitud en relación con una unidad de medida preestablecida como patrón.

Ahora bien, cualquier valor obtenido en una medición está condicionado por posibles errores caracterizados como accidentales y sistemáticos.

Un error es la diferencia entre el valor medido y el valor verdadero de una magnitud.

Los matemáticos estadísticos afirman que:

Ninguna medida es exacta.

Toda medida tiene errores.

El valor verdadero de una medición nunca se conoce.

El error exacto que se encuentra en cualquier medida siempre será desconocido.

Efectivamente, la medida de una magnitud física, obtenida de forma directa o mediante una ecuación a través de su relación con otras magnitudes medidas directamente, nunca puede ser exacta, debido a la limitada precisión de los instrumentos de medida y a una serie de factores de naturaleza diversa. Por tanto, debe aceptarse el hecho de que es prácticamente imposible conocer el valor exacto de una magnitud. Es por esta razón que, en general, en los procesos de fabricación se aceptan como valores exactos de la magnitud aquellos que están dentro de dos valores límite, considerados como tolerancia de la medida.

Los errores producidos en la medición de una magnitud pueden clasificarse en tres tipos en función del observador, según las circunstancias en que se está midiendo y según la calidad del aparato que se utiliza:

Los errores sistemáticos: son errores repetitivos que se producen en el transcurso de una medición por factores comprendidos en el sistema de medición y que afectan a los resultados finales siempre en un mismo sentido. Son debidos a errores en la calibración o a la sensibilidad de los aparatos de medida utilizados, al uso incorrecto o inapropiado de fórmulas de cálculo o a condiciones de medición inadecuadas cuando se emplean los instrumentos de medida bajo condiciones ambientales diferentes a las recomendadas por el fabricante.

Los errores accidentales o aleatorios: son errores imposibles de controlar y de conocer o determinar su causa. Son debidos a causas imprevistas o al azar y que alteran, por exceso o por defecto, la medida realizada. Se producen en la apreciación por limitaciones visuales del observador o por cambios bruscos de las condiciones ambientales.

Los errores ilegítimos o equivocaciones: son errores producidos por despistes o incorrecciones en el uso de unidades y múltiplos.

La magnitud es la propiedad medible de cualquier objeto. A la cantidad de referencia se la denomina unidad y al sistema en el que se basa dicha unidad se le denomina patrón. Por tanto, la longitud, el volumen, la masa o la cantidad de producto, son claros ejemplos de magnitudes mensurables.

Se denomina proporción numérica o regla de la proporcionalidad a la relación que guardan entre sí dos magnitudes mensurables en la que se muestran los tamaños relativos entre dos o más valores.

Definición

Proporción

Es la igualdad de dos razones.

Así, a y b son dos magnitudes mensurables que se pretenden relacionar.

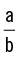
Se denomina razón geométrica (o, simplemente, razón) entre dos valores numéricos, a y b (siempre que b ≠ 0) al cociente (el resultado de dividirlos) de los dos. Una razón no tiene unidades, ya que sirve para comparar magnitudes mensurables que, en todo caso, tendrán las mismas unidades y, por tanto, se eliminarán. Pero además, la razón tan sólo indica el número de veces que una cantidad es más grande o más pequeña que otra.

La diferencia entre una fracción y una razón es que, tanto en el numerador como en el denominador, una fracción consta de números enteros, mientras en una razón el numerador y el denominador pueden estar formados por números enteros, decimales, fraccionarios, etcétera.

Las magnitudes mensurables a y b tienen ahora los valores 10 y 2, que se relacionan a razón de 5.

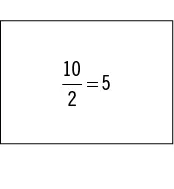
Así, cuando se presentan dos razones, para ser comparadas entre sí, para ver como se comportan entre ellas, se estará hablando de proporciones numéricas. Por tanto, una proporción es la igualdad que existe entre dos o más razones.