Álvaro Andrés Pulido Castrillón - Microeconomía del equilibrio general

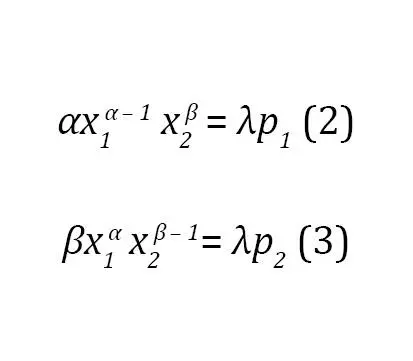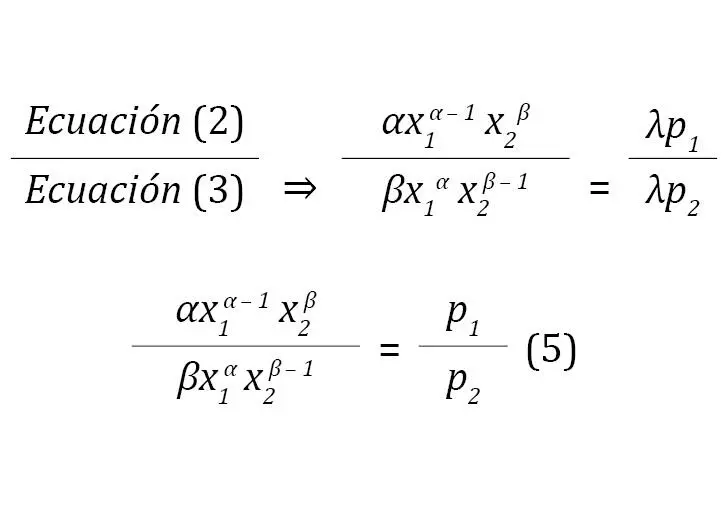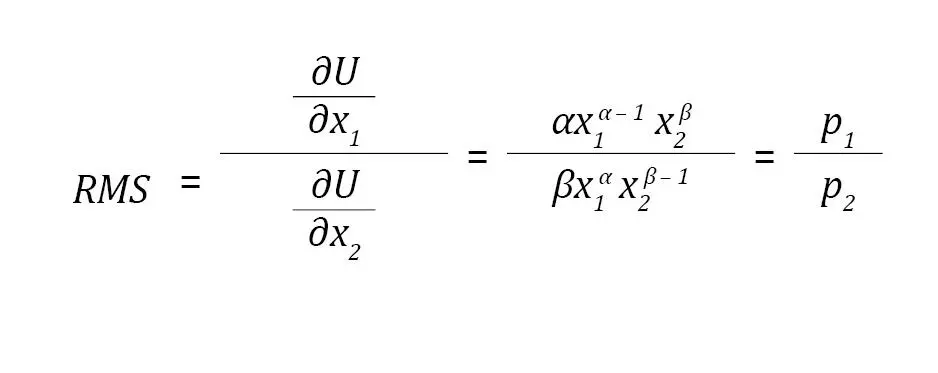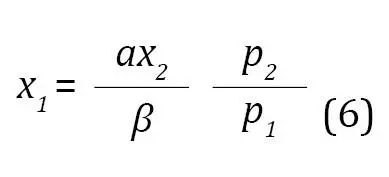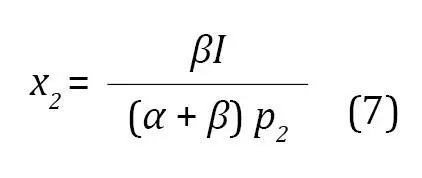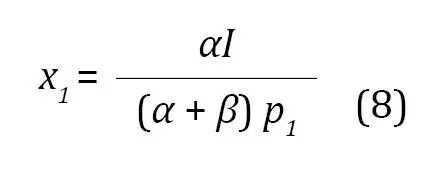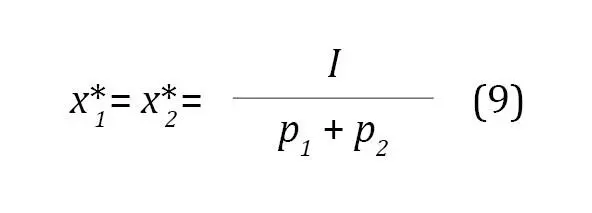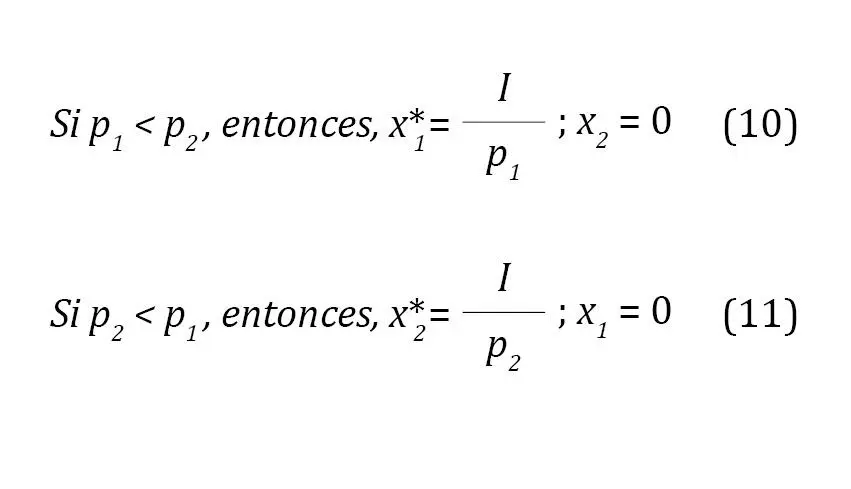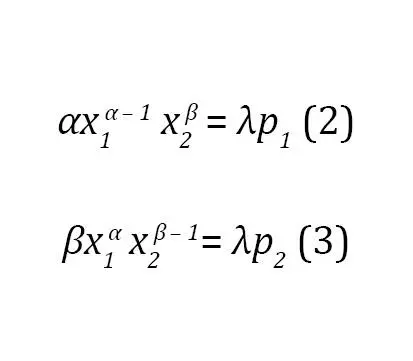
Ahora, la solución del modelo implica que al combinar las ecuaciones resultantes se obtiene la relación marginal de sustitución entre las mercancías (combinar ecuaciones):

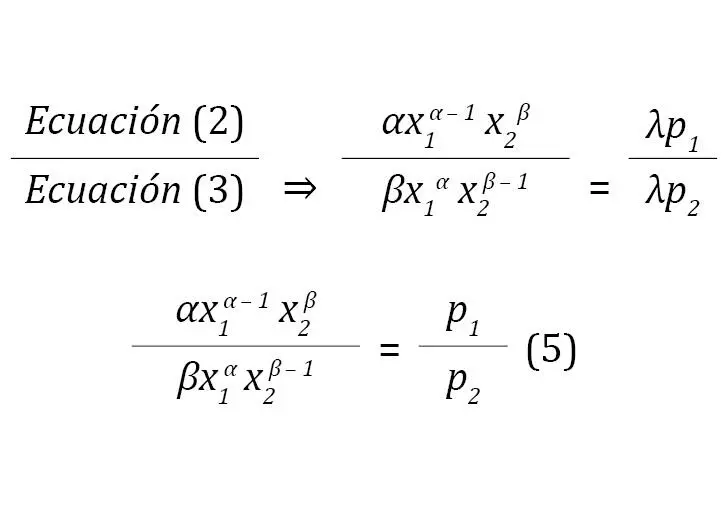
La ecuación (5) indica que la relación de precios (precios relativos) es equivalente a la de utilidades marginales, denominada relación marginal de sustitución (RMS), definida por Pindyck y Rubinfeld (2013) como la “cantidad de un bien a la que está dispuesta a renunciar una persona para obtener una unidad más de otro” (p. 705):

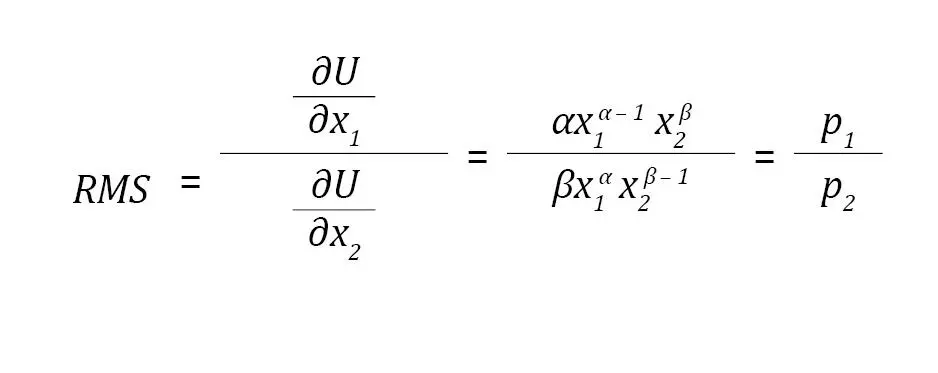
De la ecuación (5), después de un poco de álgebra y de despejar para x1, se obtiene la ecuación (6):

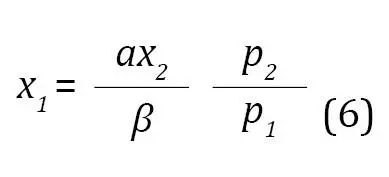
Si se reemplaza la ecuación (4) en la (6) y se despeja para x2, se llega a la ecuación (7), que refleja la demanda ordinaria de la mercancía x2:

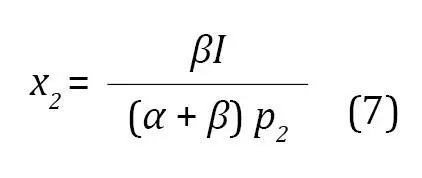
De nuevo, con un poco de álgebra, y combinando las ecuaciones (6) y (7), se tiene la demanda ordinaria de la mercancía x1 (ecuación 8):

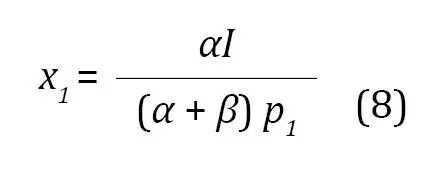
Desde el punto de vista gráfico, el proceso de optimización restringido desarrollado se sintetiza en la figura 1.5.

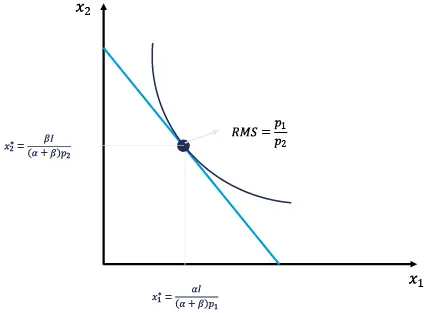
Figura 1.5. Demandas ordinarias óptimas en el caso Cobb-Douglas

Fuente: el autor.

1.5.2. Caso 2: función tipo Leontief (x1, x2 ≥ 0)

El problema del consumidor se reduce a la maximización de U(x1, x2) = Mín{x1, x2}, sujeta a la restricción de presupuesto p1 x1 + p2 x2 = I. Dado que la función de utilidad U(x1, x2) = Mín(x1, x2) es no diferenciable y no continua, el método de Lagrange no aplica; así, la solución es analítica. La restricción de presupuesto y la forma funcional de la función permiten encontrar el óptimo (figura 1.6).

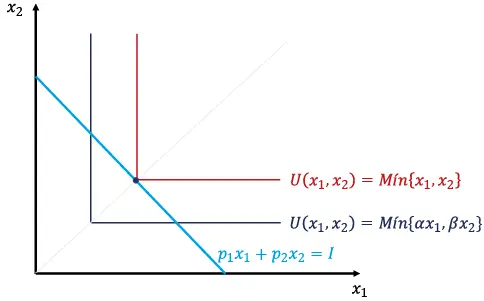
Figura 1.6. Demandas ordinarias óptimas en el caso Leontief

Fuente: el autor.

La solución analítica implica que la restricción de presupuesto debe “encontrarse” con el vértice de la función de utilidad, lo cual indica que las demandas en el óptimo para los dos bienes son equivalentes o de proporciones fijas, es decir, x*1 = x*2 . Esto se expresa en la ecuación (9) a partir de la restricción:

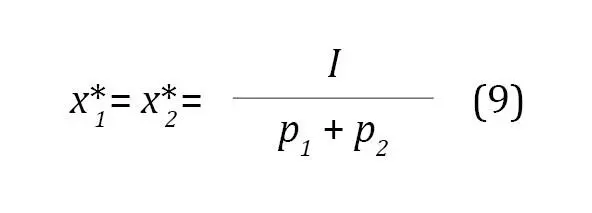
En microeconomía la demanda de cada una de las mercancías no solo depende del ingreso del consumidor y del precio de mercado, sino también del precio de la otra mercancía considerada en la cesta de consumo x. Esta situación refleja las condiciones de complementariedad perfecta entre x1 y x2, como ya se explicó.

1.5.3. Caso 3: función lineal (x1, x2 ≥ 0)

En este caso, la función de utilidad lineal de la forma U(x1, x2) = x1 + x2, bajo la restricción conocida, es diferenciable una sola vez; pero la condición de máximo conlleva que la derivada segunda debe existir, que el método de Lagrange no se puede implementar.

Lo expuesto significa que la solución es analítica (solución en la restricción), puesto que la función lineal de utilidad muestra que las mercancías son sustitutivas entre sí de manera perfecta. Esto se da “cuando un bien sustituye perfectamente al otro en el consumo, sin ninguna diferencia esencial” (Monsalve, 2016, p. 31).

La sustituibilidad perfecta implica que la decisión del consumidor, en términos de elección, se realiza según los precios de cada una de las mercancías: si p1 > p2, la demanda ordinaria se concentra en x2 y viceversa, como se especifica en las ecuaciones 10 y 11 (figura 1.7):

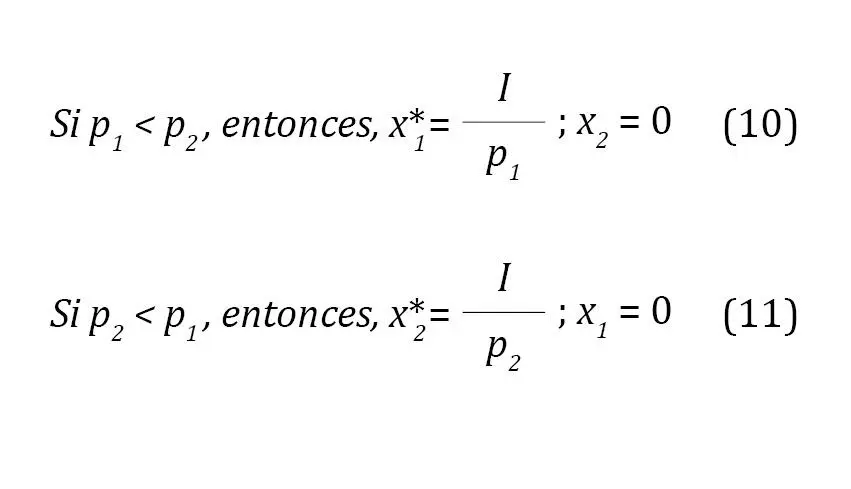
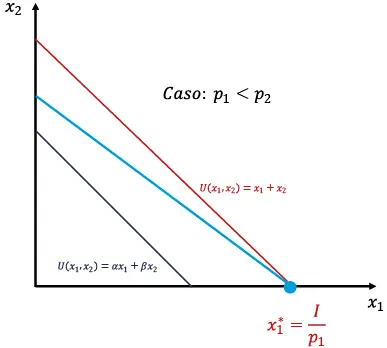
Figura 1.7. Demandas ordinarias óptimas en el caso lineal

Fuente: el autor.

1Se dice que un subconjunto cualquiera que pertenece a ℝ+ es convexo “si el segmento de recta que une cada par de puntos del conjunto está dentro del conjunto” (Lozano, 2017, p. 41).

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.