– complexity of the trained model: this defines the number of operations to be performed for a set of samples (e.g. an input image) upon inference. For example, in the case of neural networks, the complexity depends on the number of layers in a graph, the sizes of the (multidimensional) input and output maps for each layer, and the number of weights to be applied in the calculation of the output maps. A lowcomplexity neural network has less than 10 layers, while a high-complexity neural network can have tens of layers (Szegedy et al. 2015).
Table 1.1 shows input data rates and model complexities for several example machine learning applications.
Table 1.1. Input data rates and model complexities for example machine learning applications
| Machine learning application |
Input data rate |
Complexity of trained model |
| Human activity recognition |
10s Hz (few sensors) |
Low to medium |
| Voice control |
10s kHz (e.g. 16 kHz) |
Low to medium |
| Face detection |
100s kHz (low resolution and frame rate) |
Low to medium |
| Advanced computer vision |
100s MHz (high resolution and frame rate) |
High |
As can be seen from Table 1.1, input data rates and model complexities can vary significantly. As a result, the compute requirements for machine learning inference can differ by several orders of magnitude. In this chapter, we focus on machine learning inference with low-to-medium compute requirements. More specifically, we target machine learning inference that can be used to build smart low-power IoT edge devices.
In the next section, we further detail the requirements for the efficient implementation of low/mid-end machine learning inference. Using the DSP-enhanced DesignWare ®ARC ®EM9D processor as an example, we discuss the features and capabilities of a programmable processor that enable efficient execution of computations often used in machine learning inference. We further present an extensive library of software functions that can be used to quickly implement inference engines for a wide array of machine learning applications. Benchmarks are presented to demonstrate the efficiency of machine learning inference implemented using this software library that executes on the ARC EM9D processor.
1.3.1. Requirements for low/mid-end machine learning inference
IoT edge devices that use machine learning inference typically perform different types of processing, as shown in Figure 1.2.

Figure 1.2. Different types of processing in machine learning inference applications
These devices typically perform some pre-processing and feature extraction on the sensor input data before performing the actual neural network processing for the trained model. For example, a smart speaker with voice control capabilities may first pre-process the voice signal by performing acoustic echo cancellation and multimicrophone beam-forming. It may then apply FFTs to extract the spectral features for use in the neural network processing, which has been trained to recognize a vocabulary of voice commands.
1.3.1.1. Neural network processing
For each layer in a neural network, the input data must be transformed into output data. An often used transformation is the convolution , which convolves, or, more precisely, correlates, the input data with a set of trained weights. This transformation is used in convolutional neural networks (CNNs), which are often applied in image or video recognition.
Figure 1.3 shows a 2D convolution, which performs a dot-product operation using the weights of a 2D weight kernel and a selected 2D region of the input data with the same width and height as the weight kernel. The dot product yields a value (M23) in the output map. In this example, no padding is applied on the borders of the input data, hence the coordinate (2, 3) for the output value. For computing the full output map, the weight kernel is “moved” over the input map and dot-product operations are performed for the selected 2D regions, producing an output value with each dot product. For example, M24 can be calculated by moving one step to the right and performing a dot product for the region with input samples A24–A26, A34–A36 and A44–A46.

Figure 1.3. 2D convolution applying a weight kernel to input data to calculate a value in the output map
Input and output maps are often three-dimensional. That is, they have a width, a height and a depth, with different planes in the depth dimension typically referred to as channels . For input maps with a depth > 1, an output value can be calculated using a dot-product operation on input data from multiple input channels. For output maps with a depth > 1, a convolution must be performed for each output channel, using different weight kernels for different output channels. Depthwise convolution is a special convolution layer type for which the number of input and output channels is the same, with each output channel being calculated from the one input channel with the same depth value as the output channel. Yet another layer type is the fully connected layer, which performs a dot-product operation for each output value using the same number of weights as the number of samples in the input map.
The key operation in the layer types described above is the dot-product operation on input samples and weights. It is therefore a requirement for a processor to implement such dot-product operations efficiently. This involves efficient computation, for example, using MAC instructions, as well as efficient access to input data, weight kernels and output data.
CNNs are feed-forward neural networks. When a layer processes an input map, it maintains no state that impacts the processing of the next input map. Recurrent neural networks (RNNs) are a different kind of neural network that maintain the state while processing sequences of inputs. As a result, RNNs also have the ability to recognize patterns across time, and are often applied in text and speech recognition applications.
There are many different types of RNN cells from which a network can be built. In its basic form, an RNN cell calculates an output as shown in equation [1.1]:
[1.1] 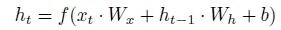
where x tis the frame t in the input sequence, h tis the output for x t, W xand W hare weight sets, b is a bias, and f () is an output activation function. Thus, the calculation of an output involves a dot product of one set of weights with new input data and another dot product of another set of weights with the previous output data. Therefore, also for RNNs, the dot product is a key operation that must be implemented efficiently. The long short-term memory (LSTM) cell is another well-known RNN cell. The LSTM cell has a more complicated structure than the basic RNN cell that we discussed above, but the dot product is again a dominant operation.
Читать дальше