In a review [145] of a book [31], Laurent Schwartz stated:
Each of us [Schwartz and Emery] tried to help the probabilists absorb stochastic infinitesimal calculus of the second order “without tears”; I don't know whether any of us succeeded or will succeed .
This book is a further effort in this direction.
The action functionals of quantum mechanics (see (8.7), page below) are analogous to stochastic integrals. They appear as integrands in the infinite‐dimensional integrals used by R.P. Feynman in his theory of quantum mechanics and quantum electrodynamics.
In comparison with alternative approaches such as those of J. Schwinger ([147–150]) and S. Tomonaga ([88–92, 164, 165]), Feynman's method is said to be physically intuitive. It contrasts with the mathematics‐leaning approach of Paul Dirac [27]:
The present lectures, like those of Eddington, are concerned with unifying relativity and quantum theory, but they approach the question from a different point of view. Eddington's method is first to get the physical ideas clear and then gradually to build up a mathematical scheme. The present method is just the opposite—first to set up a mathematical scheme and then try to get its physical interpretation .
In reading [FH] it can be helpful to bear in mind that “[Feynman was] the outstanding intuitionist of our age …” , (attributed to Schwinger in [32]).
Feynman's first published paper on path integrals was [F1], Space‐time approach to non‐relativistic quantum mechanics [39]. In a long tradition of the relationship between physics and mathematics it entailed problems of a pure mathematical kind:
There are very interesting problems involved in the attempt to avoid the subdivision and limiting processes [in Feynman's construction of path integrals]. Some sort of complex measure is being associated with the space of functions 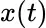 . Finite results can be obtained under unexpected circumstances because the measure is not positive everywhere, but the contributions from most of the paths largely cancel out. These curious mathematical problems are largely side‐stepped by the subdivision process. However, one feels as Cavalieri must have felt calculating the volume of a pyramid before the invention of calculus . [39] (R.P. Feynman [F1]; also page 79 of [10].)
. Finite results can be obtained under unexpected circumstances because the measure is not positive everywhere, but the contributions from most of the paths largely cancel out. These curious mathematical problems are largely side‐stepped by the subdivision process. However, one feels as Cavalieri must have felt calculating the volume of a pyramid before the invention of calculus . [39] (R.P. Feynman [F1]; also page 79 of [10].)
These are problems essentially of mathematics, not physics or quantum mechanics. And the solutions proposed in [MTRV], and here, are intended to be contributions to mathematics, not physics.
The space of functions (for ) is where is the set of real numbers and . It is likely that Feynman's reference to “measure” above relates to Lebesgue‐type measure on measurable subsets of , which is not available in the form suggested by Feynman. Here are some mathematical issues:
Instead of measurable sets and measure of sets, [MTRV] provides a solution based on a structure of interval‐type subsets of , with a “natural” volume function for such subsets, and using the ‐complete system of non‐absolute integration described in [MTRV].
Feynman's statement that “the contributions from most of the paths largely cancel out” suggests a non‐absolute convergence approach, and confirms the unsuitability of methods requiring absolute convergence.
Stochastic integrals sometimes have the form where is a stochastic process. Feynman's integrals often include expressions involving the integral of kinetic energy . These are action functionals, integrals such aswhere the latter has the form of a stochastic integral . Generally speaking, for , is non‐differentiable. So none of these functionals actually exists as an integral and, in order to give mathematical meaning to them, various devices have to be used, such as the weak integrals of classical stochastic calculus, or Feynman's subdivision and limiting processes.
Feynman's “subdivision and limiting processes” are described in [F1], and in [FH] (Quantum Mechanics and Path Integrals [46], by R.P. Feynman and A.R. Hibbs). They are also examined in section 7.18 of [MTRV], along with their relationship 6to the ‐complete integral solution.
This book provides an alternative solution to these problems. Instead of integrals 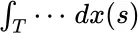 , or
, or  , sample times
, sample times 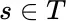 are used to form Riemann sums. These are called stochastic sums in the stochastic integral case, and sampling sums in the case of action integrals:
are used to form Riemann sums. These are called stochastic sums in the stochastic integral case, and sampling sums in the case of action integrals:
These functionals are finite sums, not integrals;
they are sample versions of stochastic integrals (or of action integrals in the case of quantum mechanics);
they always exist;
and their expected values and other properties are defined and calculated by a well defined system of ‐complete (or gauge) integration in .
And, just as it is reasonable to estimate integrals by means of finite Riemann sums, it is equally reasonable to use finite samples to estimate the functional integrands by means of finite samples (or sampling sums).
This book considers mathematical aspects of the Feynman integral theory as it is expounded in [FH], which starts with
a single particle interacting with a conservative mechanical force,
and which progresses through to a system consisting of the interaction of a charged particle with an electromagnetic field .
For the latter system, [FH] declares that a certain action functional should be integrated over “all degrees of freedom” of the system—over all possible values of each of the variables.
This highly intuitive mode of expression is physically suggestive and resonant. But in mathematics a domain of integration must be defined and formulated as a definite mathematical set composed of definite mathematical elements or points.
In [FH] as in [MTRV] this is achieved for motion 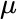 by translating “integration over all degrees of freedom” of the single particle motion into integration on a domain
by translating “integration over all degrees of freedom” of the single particle motion into integration on a domain 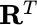 consisting of elements or points
consisting of elements or points 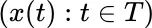 ; or, simply,
; or, simply, 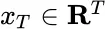 . (This deals only with one‐dimensional particle motion. For physical realism elements of the domain should be points
. (This deals only with one‐dimensional particle motion. For physical realism elements of the domain should be points 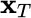 of
of 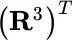 , where
, where
Читать дальше

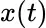 . Finite results can be obtained under unexpected circumstances because the measure is not positive everywhere, but the contributions from most of the paths largely cancel out. These curious mathematical problems are largely side‐stepped by the subdivision process. However, one feels as Cavalieri must have felt calculating the volume of a pyramid before the invention of calculus . [39] (R.P. Feynman [F1]; also page 79 of [10].)
. Finite results can be obtained under unexpected circumstances because the measure is not positive everywhere, but the contributions from most of the paths largely cancel out. These curious mathematical problems are largely side‐stepped by the subdivision process. However, one feels as Cavalieri must have felt calculating the volume of a pyramid before the invention of calculus . [39] (R.P. Feynman [F1]; also page 79 of [10].)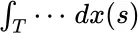 , or
, or  , sample times
, sample times 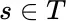 are used to form Riemann sums. These are called stochastic sums in the stochastic integral case, and sampling sums in the case of action integrals:
are used to form Riemann sums. These are called stochastic sums in the stochastic integral case, and sampling sums in the case of action integrals: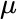 by translating “integration over all degrees of freedom” of the single particle motion into integration on a domain
by translating “integration over all degrees of freedom” of the single particle motion into integration on a domain 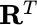 consisting of elements or points
consisting of elements or points 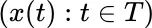 ; or, simply,
; or, simply, 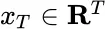 . (This deals only with one‐dimensional particle motion. For physical realism elements of the domain should be points
. (This deals only with one‐dimensional particle motion. For physical realism elements of the domain should be points 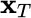 of
of 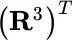 , where
, where










