Classification: LCC QA274.2 .M85 2020 (print) | LCC QA274.2 (ebook) | DDC 519.2/2‐dc23
LC record available at https://lccn.loc.gov/2020016333
LC ebook record available at https://lccn.loc.gov/2020016334
Cover Design: Wiley
Cover Image: © bannerwega/Getty Images
Set in 9.5/12.5pt STIXTwoText by SPi Global, Chennai, India
This book is about infinite‐dimensional integration in stochastic calculus and in quantum electrodynamics, using the gauge integral technique pioneered by R. Henstock and J. Kurzweil.
A link between stochastic calculus and quantum mechanics is provided in a previous book by the author ([121], A Modern Theory of Random Variation , or [MTRV] for short), which establishes a mathematical connection between large scale Brownian motion on the one hand and, on the other, small scale quantum level phenomena of particle motion subject to a conservative external mechanical force. In [MTRV] each of the two subjects is a special case of 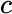 ‐Brownian motion .
‐Brownian motion .
The present book is a continuation of [MTRV], in the sense that it develops and extends some of the themes of that book. On the other hand this book is a stand‐alone introduction to particular problems of integration in the probabilistic theory of stochastic calculus, and in the probability‐like theory of quantum mechanics.
Between [MTRV] and this book there is a significant difference in style of exposition. Practically all the underlying mathematical theory is already set out in [MTRV]. The present book includes motivational explanation of the key points of the underlying mathematical theory, along with ample illustrations of the calculus—the routine procedures—of the gauge theory of integration.
But because the “mathematical heavy lifting” (or rigorous mathematical underpinning) is already accomplished in [MTRV], the present book can take a more gradual, relaxed, and discursive approach which seeks to engage the reader with the subject by exploring a much smaller range of chosen themes.
Thus there is hardly anything of the formal Theorem‐Proof structure in this book. Instead the text is organised around Examples with accompanying introductions and explanation, illustrating themes from probability and physics which can be difficult and taxing. Particular areas of interest in the book can be selected and read without engaging with other topics. Its relatively self‐contained component parts can easily be “dipped into”.
In addition to [MTRV], two principal physics sources for this book are [39], Space‐time approach to non‐relativistic quantum mechanics (cited as [F1] for short) by R. Feynman; and [46], Quantum Mechanics and Path Integrals (cited as [FH] for short) by R. Feynman and A. Hibbs.
Certain modes of expression used by physicist R. Feynman are highly illuminating—but from a physics perspective. For instance: Integrate [some expression] over all degrees of freedom [all variables] of the [physical] system . This statement does not specify the mathematical domain  for this integration process, nor how
for this integration process, nor how 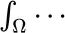 (the integral on
(the integral on  ) is to be actually calculated.
) is to be actually calculated.
For quantum electrodynamics, and with 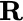 denoting the real line and
denoting the real line and 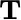 an interval of time, this book proposes a product space domain
an interval of time, this book proposes a product space domain
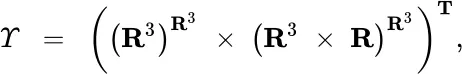
along with methods of calculating integrals on product spaces such as
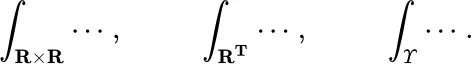
The examples, explanations, and illustrations of this book, though prompted by issues in physics and finance, are primarily about underlying mathematical problems. A reader whose primary purpose is to investigate finance or physics as such should seek out other, more relevant sources.
Also, it is inadvisable to approach the gauge or Riemann sum theory of integration as if it were unchallenging or easy compared with, say, Lebesgue's integration theory. That said, the general idea of gauge integration is more accessible (initially, at least) than the mathematical theory of measure which underpins other approaches to integration. (Gauge integration theory includes measure and measurability—see section A.1 of [MTRV]—but these are outcomes rather than prerequisites of the theory.)
Another central theme of this book is to devise new and better versions of stochastic integrals. Functionals of the form 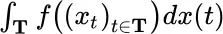 appear in both the theory of stochastic processes (as stochastic integral) and quantum theory (as integral of lagrangian function, or system action).
appear in both the theory of stochastic processes (as stochastic integral) and quantum theory (as integral of lagrangian function, or system action).
Such integral functionals either do not actually exist, or are not easy to define. In their place, this book proposes replacement or equivalent functionals which involve Riemann sums rather than integrals. In the case of stochastic processes such sums are called stochastic sums . In quantum theory they are designated sampling sums . (The former are a special case of the latter.)
The general idea of infinite‐dimensional integration on a Cartesian product domain can be found in chapter 3of [MTRV]. The technical foundations of the subject are in chapter 4of that book.
The core of this book consists of Chapters 6and 9. Without tackling the companion book [MTRV], a reader who wants a quick introduction to basic gauge integral theory can get it in Chapter 10below. This includes a re‐definition of the standard Lebesgue integral (on an abstract measure space) as a Riemann‐Stieltjes integral 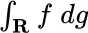 on domain
on domain 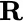 .
.
There is a website for commentary on technical issues: https://sites.google.com/site/StieltjesComplete/  " >cited as [
" >cited as [ website] in this book. Technical communications are welcome and can be addressed to:
stieltjes.complete.integral@gmail.com
Pat Muldowney
The term “gauge” in the title relates to gauge integration in mathematics (a generalized form of Riemann integration). It is not about gauge symmetry or gauge transformations in theoretical physics.
Читать дальше

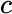 ‐Brownian motion .
‐Brownian motion . for this integration process, nor how
for this integration process, nor how 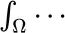 (the integral on
(the integral on  ) is to be actually calculated.
) is to be actually calculated.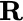 denoting the real line and
denoting the real line and 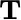 an interval of time, this book proposes a product space domain
an interval of time, this book proposes a product space domain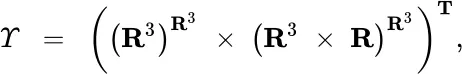
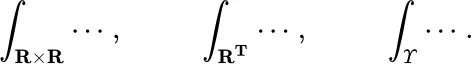
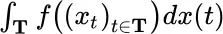 appear in both the theory of stochastic processes (as stochastic integral) and quantum theory (as integral of lagrangian function, or system action).
appear in both the theory of stochastic processes (as stochastic integral) and quantum theory (as integral of lagrangian function, or system action).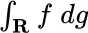 on domain
on domain 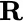 .
. " >cited as [
" >cited as [ 










