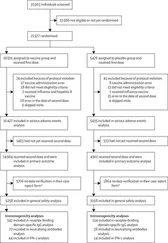
One problem is that this process tends to selectively exclude patients with the more severe disease. Evidence for selective exclusion of patients following such reviews is provided by Machin, Stenning, Parmar, et al . (1997) who examined the published and pioneering portfolio of the early randomised trials conducted by the UK Medical Research Council in patients with cancer. They showed that the earlier publications systematically excluded patients from analysis and hence reported on fewer patients in the more aggressive treatment arm, despite a 1 : 1 randomisation. Thus, for example, any patient who had difficulties with this treatment, perhaps the sicker patients, were not included in the assessment of its efficacy and this systematic exclusion would tend to bias the results in its favour.
However, in certain circumstances, a per‐protocol summary of the trial results may be more relevant. In such an analysis, the comparison is made only in those patients who comply (which has to be carefully defined in advance) with the treatment allocated. One example of a per‐protocol analysis is if the toxicity and/or side effects profile of a new agent are to be compared. In this circumstance, an ITT analysis including those patients who were randomised to the drug but then did not receive it (for whatever reason) could seriously underestimate the true scale of the relative safety profiles. If a per‐protocol analysis is appropriate for such endpoints, then the trial protocol should state that such an analysis is intended from the onset. One situation where a per‐protocol analysis is important is when reporting the results of non‐inferiority trials that we discuss in Chapter 15.
Once it is clear which patients are to be included in the final analysis, any exclusions after randomisation should be accounted for, described and justified in concordance with the CONSORT statement. Only then can work on the analysis and the trial publication be started. However, it is usually expedient to plan and prepare preliminary analyses prior to the final endpoint analysis, so that the results of the trial can be disseminated with the minimum of delay. Since the structure of research publications often takes a familiar format (indeed investigators should have a target clinical journal in mind even at the design stage), key items can be prepared in advance and some of these will be based on sections of the trial protocol itself as we will list in Figure 3.1. If nothing else, the protocol will provide much of the text outlining the background and purpose of the trial, the details of eligible patients, the interventions studied, the randomisation process, a sample size justification, key elements of the analytical methods and a list of some important references. Further, if the trial progress is monitored regularly with feed‐back reports to the investigating team, then these reports can form the basis for some tabular and graphical presentations that will be included in the final publication. Clearly, the responsible writing committee will have to amend and update some of these details as appropriate and the eventual presentation of results and ultimate discussion will depend on the trial findings.
2.10 Technical details
2.10.1 Statistical models
Whatever the type of trial, it is usually convenient to think of the underlying structure of the design in terms of a statistical model. This model encapsulates the question we are intending to answer. Once the model is specified, the object of the corresponding clinical trial (and hence the eventual analysis) is to estimate the parameters of this model as precisely as is reasonable.
Suppose in a particular trial, we wish to compare two treatments, Standard ( S ) and Test ( T ). We can use an indicator variable to identify the treatment received by a patient, by setting x = 0 and x = 1 for the two treatments respectively. If the outcome of interest is a continuous variable, y , then this is related to the treatment or intervention by the linear regression equation
(2.1) 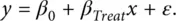
In this equation, β 0and β Treatare constants and are termed the parameters of the model. Here, β Treatis the coefficient which represents the magnitude of the difference between the treatments and so to determine its value is the major focus for the clinical trials. In contrast, ε represents the noise (or error) and this is assumed to be random and have an independent Normal distribution with mean value 0 across all subjects recruited to the trial and standard deviation ( SD ), σ . The object of a trial would be to estimate β 0and β Treat, and we write such estimates as b 0and b Treatto distinguish them from the corresponding parameters.
Given a set of pairs of observations ( x 1, y 1), ( x 2, y 2), …, ( x n, y n) from n individuals, the regression coefficient of β Treatis estimated by
(2.2) 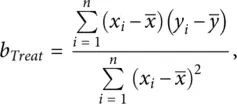
and the intercept by
(2.3) 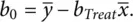
The corresponding SD is estimated by
(2.4) 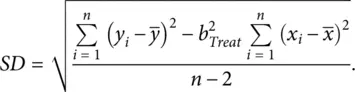
On the basis of model (2.1), the two fundamental issues in trial design to consider are as follows:
1 What levels of the design variable x to choose?
2 How many subjects should we recruit?
In this model, with x = 0 for the standard or control treatment, S , y 0= β 0and this represents the ‘true’ or population mean of this group, labelled μ S. Alternatively, with x = 1, the sum y 1= β 0+ β Treatrepresents μ Tthe population mean of group T . Thus, the difference, δ , between those receiving S and T , is y 1− y 0= β 0+ β Treat− β 0= β Treat. From this β Treat= μ T− μ Sand β 0= μ S. Population means are estimated by sample means, in this case 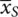 and
and 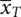 so that the estimates of the parameters are b 0=
so that the estimates of the parameters are b 0= 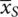 and b Treat=
and b Treat= 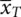 −
− 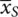 . The latter is the estimate of the true difference between treatments, δ = μ T− μ S.
. The latter is the estimate of the true difference between treatments, δ = μ T− μ S.
Читать дальше

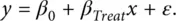
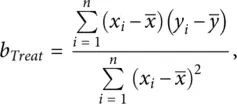
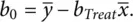
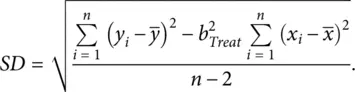
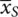 and
and 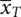 so that the estimates of the parameters are b 0=
so that the estimates of the parameters are b 0= 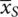 and b Treat=
and b Treat= 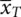 −
− 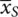 . The latter is the estimate of the true difference between treatments, δ = μ T− μ S.
. The latter is the estimate of the true difference between treatments, δ = μ T− μ S.