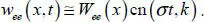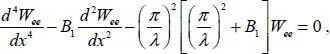1 ...6 7 8 10 11 12 ...15 Many papers are devoted to multi-span plates (Moskalenko and Chen 1965; Moskalenko 1968, 1969; Elishakoff and Steinberg 1979; Elishakoff et al . 1993).
Dynamics of cylindrical, conical and shallow spherical shells were analyzed in Bolotin (1960b, 1961c, 1984), Gavrilov (1961a), Zhinzher (1975) and Elishakoff and Wiener (1976).
One of the problems of the DEEM application is the degeneracy of DEE when decaying solutions cannot be constructed for some wave numbers (Bolotin 1984). The resolution of this problem was proposed in Elishakoff (1974) and Elishakoff and Wiener (1976). The solution of the original problem is represented as a sum of solutions of two subproblems. Each of these solutions satisfy the boundary conditions at two opposite boundaries only. The matching conditions described in Bolotin’s original papers (Bolotin 1960a, 1960b, 1961a, 1961b, 1961c) are not used, and it gives us the possibility to avoid difficulties caused by the degeneracy of DEEM.
Thereby, we note the following point. Asymptotic methods can be used in two versions (Andrianov et al . 2014). From the very beginning, a small parameter can be introduced into the PDEs or ODEs and then asymptotic fractional analysis (Kline 1965) can be used. However, we can use variational approaches (Rayleigh–Ritz, Bubnov–Galerkin, Kantorovich, Trefftz, etc.) to solve the original problem and reduce it to the infinite systems of coupled ODEs or algebraic equations. Then, a small parameter, caused by the physical nature of the problem or an artificial (homotopy) one, can be introduced into the infinite system to split it into simplified subsystems. The second approach makes it possible to avoid the degeneracy of DEE.
Other generalizations of DEEM are described in the following sections.
1.4. Generalization for the nonlinear case
To describe the generalization of DEEM to the nonlinear case, we use the nonlinear Kirchhoff beam equation (Kauderer 1958):
[1.19] 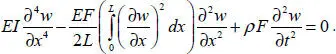
Let the beam be elastically supported:
[1.20] 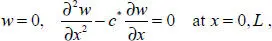
where c *= c/EI , c is the coefficient characterizing elastic support.
We search a generating solution in the form
[1.21] 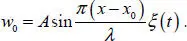
Substituting ansatz [1.21]into PDE [1.19], we obtain an ODE for determining the time function ξ ( t ) :
[1.22] 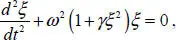
where
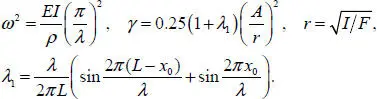
ODE [1.22]with initial conditions
[1.23] 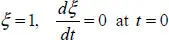
has the solution
[1.24] 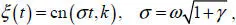
where cn( σt , k ) is the Jacobi cosine elliptic functions with period T = 4 K ,  is the complete elliptic integral of the first kind with modulus
is the complete elliptic integral of the first kind with modulus 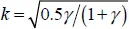 (Abramowitz and Stegun 1965).
(Abramowitz and Stegun 1965).
The solution to the problem far from the edges is
[1.25] 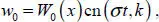
where 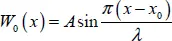 .
.
Solution [1.25]satisfies the original equation [1.19], but does not satisfy the boundary conditions [1.20]. To construct the states localized near the edges, we represent the solution of the original problem in the form
[1.26] 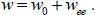
Substituting ansatz [1.26]into ODE [1.19], we obtain
[1.27] 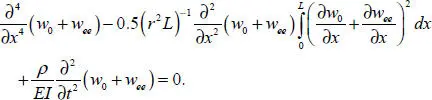
In contrast to the previously considered linear case, the equations for functions w 0and wee are coupled due to the nonlinearity of the problem. At the same time, the solution in the inner domain and EEs differ energetically since the EEs are localized in a small vicinity of the beam ends (Andrianov et al . 1979; Awrejcewicz et al . 1998; Andrianov et al . 2004, 2014). Let us estimate the orders of the integrand terms in equation [1.27]with respect to L/λ ≫ 1:
[1.28] 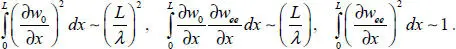
Restricting ourselves to the term of order ( π / λ ) 2≫ 1 in equation [1.27], we reduce it to the form:
[1.29] 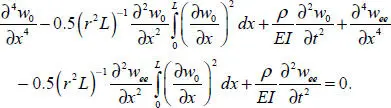
Substituting function w 0into equation [1.29], we obtain a PDE for function wee :
[1.30] 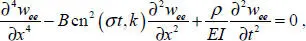
where 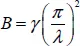 .
.
It is important that PDE [1.30]is linear. The spatial and time variables are not separated exactly; therefore, we apply the Kantorovich variational method (Kantorovich and Krylov 1958) to solve equation [1.30], presenting wee in the form
[1.31] 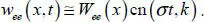
On substituting ansatz [1.31]into PDE [1.30]and applying the Kantorovich method (Kantorovich and Krylov 1958), the following ODE is obtained:
[1.32] 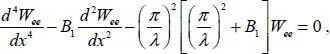
Читать дальше

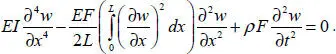
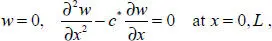
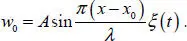
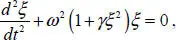
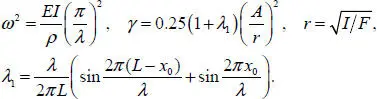
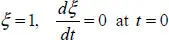
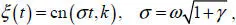
 is the complete elliptic integral of the first kind with modulus
is the complete elliptic integral of the first kind with modulus 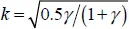 (Abramowitz and Stegun 1965).
(Abramowitz and Stegun 1965).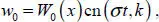
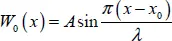 .
.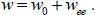
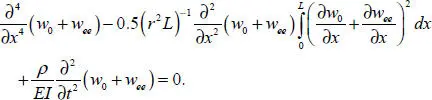
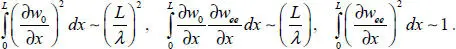
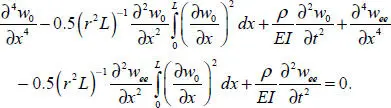
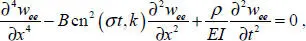
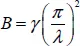 .
.