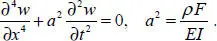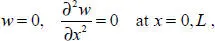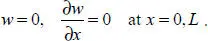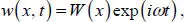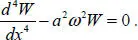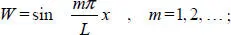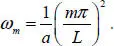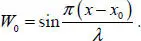Figure P.11. Elishakoff with his wife, Esther Elisha, M.D., during an ASME awards ceremony
On behalf of all the authors of this book, including those friends who were unable to contribute, we wish Prof. Isaac Elishakoff many more decades of fruitful works and collaborations for the benefit of world mechanics, in particular.
Modern Trends in Structural and Solid Mechanics 1 – the first of three separate volumes that comprise this book – presents recent developments and research discoveries in structural and solid mechanics, with a focus on the statics and stability of solid and structural members.
The book is centered around theoretical analysis and numerical phenomena and has broad scope, covering topics such as: buckling of discrete systems (elastic chains, lattices with short and long range interactions, and discrete arches), buckling of continuous structural elements including beams, arches and plates, static investigation of composite plates, exact solutions of plate problems, elastic and inelastic buckling, dynamic buckling under impulsive loading, buckling and post-buckling investigations, buckling of conservative and non-conservative systems, buckling of micro and macro-systems. The engineering applications concern both small-scale phenomena with micro and nano-buckling up to large-scale structures, including the buckling of drillstring systems.
Each of the three volumes is intended for graduate students and researchers in the field of theoretical and applied mechanics.
Prof. Noël CHALLAMEL
Lorient, France
Prof. Julius KAPLUNOV
Keele, UK
Prof. Izuru TAKEWAKI
Kyoto, Japan
February 2021
For a color version of all the figures in this chapter, see www.iste.co.uk/challamel/mechanics2.zip.
1
Bolotin’s Dynamic Edge Effect Method Revisited (Review)
A comprehensive review of Bolotin’s edge effect method is presented. This chapter begins with a toy problem and is concluded by nonlinear considerations that have not been developed by Bolotin himself. Various generalizations and modifications of the method are described, along with a variety of solved problems for which a wide list of references is provided. Attempts are also made to frame the method among the known methods for finding rapidly oscillating solutions.
Professor Isaac E. Elishakoff was a doctoral student of the world-renowned scientist V.V. Bolotin (March 29, 1926 to May 28, 2008) (Bolotin 2006). The first research works of I. Elishakoff and his PhD thesis were devoted to the application and development of the dynamic edge effect (EE) method proposed by V.V. Bolotin. After moving from the Soviet Union to the Western world, Prof. Elishakoff made great efforts to popularize the dynamic EE method in the Western scientific community (Elishakoff 1974, 1976; Elishakoff and Wiener 1976).
Therefore, the appearance of a review of papers related to Bolotin’s method in the volume devoted to Prof. Elishakoff’s 75th birthday seems quite reasonable. Moreover, the previous comprehensive reviews of the subject were published in 1976 (Elishakoff 1976) and 1984 (Bolotin 1984).
In the early 1960s, V.V. Bolotin put forward an asymptotic method for studying natural oscillations of plates and shells, which used the inverse of the dimensionless vibration frequency as a small parameter (Bolotin 1960a, 1960b). In a more general formulation, it is a method for solving self-adjoint eigenvalue problems defined in a rectangular domain, called the boundary value problems with quasi-separable variables, according to Bolotin’s terminology. For this reason, the method is referred to as Bolotin’s method or the dynamic edge effect method (DEEM). And despite the fact that 60 years have passed since the method creation, it is still relevant. The purpose of this review is describing various generalizations and modifications of DEEM, the problems solved with the use of this method and also trying to determine the place of DEEM among the known methods for finding rapidly oscillating solutions. Thus, we demonstrate that DEEM can be broadly applied for solving modern problems.
1.2. Toy problem: natural beam oscillations
Demonstrate the main idea of DEEM on a spatially 1D problem, which can be reduced to a transcendental equation and solved numerically with any degree of accuracy (Weaver et al . 1990). Consider the natural oscillations of a beam of length L , described by the following PDE:
[1.1] 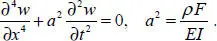
Here, w is the normal displacement, E is the Young modulus, F is the cross-sectional area of the beam, I is the axial inertia moment of the beam cross-section, and ρ is the density of the beam material.
Let us compare two versions of boundary conditions:
[1.2] 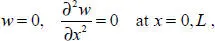
[1.3] 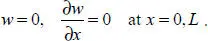
We use the following ansatz:
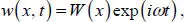
where ω is the eigenfrequency and W ( x ) is the eigenfunction.
The equation for eigenfunction W ( x ) has the form
[1.4] 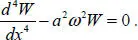
The solution of the eigenvalue problem [1.4], [1.2]is given by
[1.5] 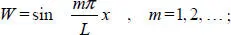
[1.6] 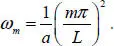
The eigenvalue problem [1.4], [1.3]does not allow separation of variables. However, if the eigenfunction oscillates rapidly along x (i.e. a rather high form of oscillations is considered), then we can hope that in this case a solution of the form [1.5]is also valid for the inner domain sufficiently distant from the boundaries ( Figure 1.1). Such an expression does not satisfy the boundary conditions. However, if the solution that compensates the residuals at the boundary conditions and decays rapidly, then the approximate expressions for the eigenfunctions and eigenfrequencies can be obtained.
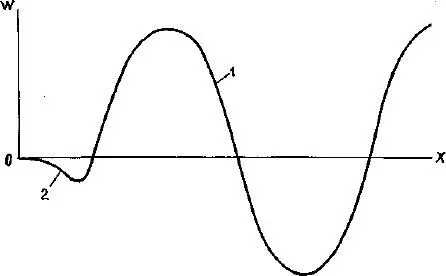
Figure 1.1. Curve 1 corresponds to the rapidly oscillating solution in the inner domain, and curve 2 corresponds to the sum of DEE and the rapidly oscillating solution
Let us suppose the solution of equation [1.4]in the form
[1.7] 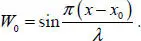
Читать дальше