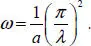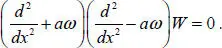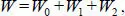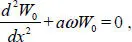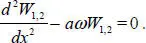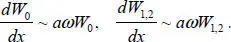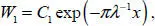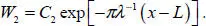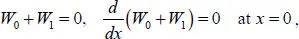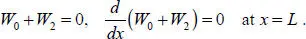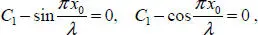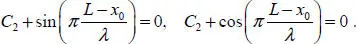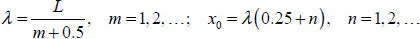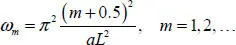Modern Trends in Structural and Solid Mechanics 2

The oscillation frequency ω is

[1.8]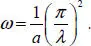

Factorization of ODE [1.4]is (Vakhromeev and Kornev 1972)

[1.9]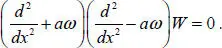

The general solution of ODE [1.9]is given by

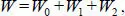
where functions W 0and W 1,2are the general solutions of the following equations:

[1.10]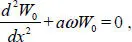

[1.11]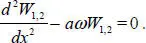

For large frequencies ( aω ≫1), the following estimates for the derivatives of functions W 0and W 1,2are obtained:

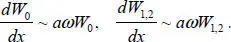
The behavior of these solution components is different: W 1is the rapidly oscillating function, and W 2is the sum of exponentials rapidly decreasing from the edges of the beam.

Therefore, the situation under consideration is fundamentally different from the case when the characteristic equation has small and large modulo roots, which is typical for boundary layer theory. In our case, we are talking about the separation of solutions, one of which oscillates at the same rate as the EE decays (i.e. the characteristic equation has large real and imaginary roots with moduli of the same order). The self-adjoint eigenvalue problem [1.1], [1.2]can be referred to as the boundary value problem with quasi-separable variables (Bolotin 1960a, 1960b, 1961a, 1961b, 1961c; Bolotin et al . 1950, 1961).

We proceed to the construction of the EE described by equation [1.11]. Taking into account the expression for the natural frequency [1.8], we obtain the following relations for EEs localized in the vicinity of the edges x = 0 and x = L , respectively:

[1.12]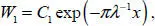

[1.13]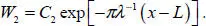

We assume that the beam is so long such that EEs do not affect each other, i.e. exp(− πλ -1 L ) ≪ 1.

Now, it remains to find the quantities x 0, λ and constants C 1, C 2from the boundary conditions to determine the eigenmodes and eigenfrequencies:

[1.14]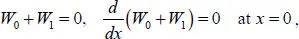

[1.15]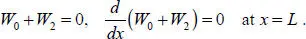

Note that in original works by Bolotin, a slightly different matching procedure is used. Namely, the matching conditions [1.14], [1.15]are not given at the domain boundaries. They are set at some points, which are then determined from the solution of the system of transcendental equations along with other unknown constants.

Substituting expressions [1.7]and [1.12]into conditions [1.14], and expressions [1.7]and [1.13]into [1.15], we obtain

[1.16]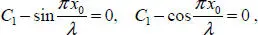

[1.17]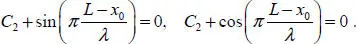

For λ and x 0, we have the following expressions:

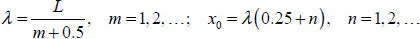
Finally, the formula for the natural oscillation frequencies of the clamped beam is written as follows:

[1.18]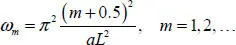

The same formula follows from the analysis of the transcendental equation (Weaver et al . 1990). Its difference from the numerical solution is less than 1% even for the first natural oscillation frequency.

Using DEEM to solve various problems proved its high accuracy even when calculating the first eigenfrequencies (Bolotin 1960a, 1960b, 1961a, 1961b, 1961c, 1961d; Gavrilov 1961a, 1961b; Bolotin 1963, 1970; Elishakoff and Wiener 1976; Elishakoff and Steinberg 1979; Emmerling 1979; Bolotin 1984; Elishakoff et al . 1993, 1994). It confirms “Crighton’s principle” (Crighton 1994):

All experience suggests that asymptotic solutions are useful numerically far beyond their nominal range of validity, and can often be used directly, at least at a preliminary product design stage, for example, saving the need for accurate computation until the final design stage where many variables have been restricted to narrow ranges.

The problem of natural oscillations was considered above. In the case of forced oscillations, the response is given as a series expansion in terms of normal modes of natural oscillations. It is important that one can use only the rapidly oscillating part of solution W 0, neglecting the dynamic edge effect (DEE) (Bolotin 1961b, 1961c, 1970, 1984).

DEEM in its original form can be effectively used for calculating natural, free and forced oscillations of rectangular plates, shells of revolution and shallow shells with a rectangular base.

In particular, DEEM is widely used for the analysis of rectangular isotropic (Bolotin et al . 1958; Bolotin 1961d, 1963; Kudryavtsev 1964; Dickinson and Warburton 1967; Bolotin 1970; King and Lin 1974; Elishakoff 1976; Emmerling 1979; Bolotin 1984; Elishakoff et al . 1994) and orthotropic (Dickinson 1971; Elishakoff 1974; Kaza and Ramaiah 1978; Vijaykumar and Ramaiah 1978) plates with various types of boundary conditions, plates on elastic foundations (Gibigaye et al . 2016), laminated and stiffened plates and panels (Lin and King 1974; Ueng and Nickels 1978; Meilani 2012, 2015). Oscillations and buckling of stressed plates were studied in Dickinson (1971, 1975), and box structures were studied in Dickinson (1975b). The Timoshenko theory of beams, and Mindlin, Reissner and Ambartsumyan theories of plates were also used in some works (Kudryavtsev 1960; Moskalenko 1961; Nelson 1978).

In the paper by Dickinson and Warburton (1967), DEEM was applied to consider free flexural vibrations of systems built up from rectangular plates.