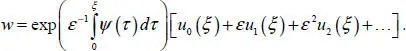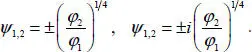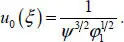The key to short-wave asymptotics is the ansatz φ ( x )exp( iε −1 S ( x )), in the nonlinear case – φ ( x )Φ( iε −1 S ( x )), where 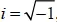 , 0 < ε ≪ 1. In the DEE method, ε = 1/ λ , where λ is the nondimensional frequency. As a result, the construction of the asymptotics can be reduced to solving the eikonal and transport equations (Birger and Panovko 1968). However, short-wave (high-frequency) asymptotics can be treated as a multiscale approach (Maslov and Fedoryuk 1981).
, 0 < ε ≪ 1. In the DEE method, ε = 1/ λ , where λ is the nondimensional frequency. As a result, the construction of the asymptotics can be reduced to solving the eikonal and transport equations (Birger and Panovko 1968). However, short-wave (high-frequency) asymptotics can be treated as a multiscale approach (Maslov and Fedoryuk 1981).
Let us show the generalization of DEEM based on the WKBJ approach using the toy problem – natural oscillation of a beam of variable cross-section (Bauer et al . 2015):
[1.55] 
with clamped edges.
In dimensionless variables, we obtain
[1.56] 
[1.57] 
where 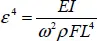 ,
, 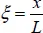 .
.
Functions φ 1, φ 2are supposed to be smooth enough to avoid turning points.
The solution to equation [1.56]is sought in the form:
[1.58] 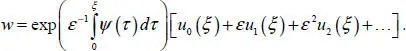
Substituting ansatz [1.58]into equation [1.56]and applying ε-splitting, we obtain a recurrent system of equations:
[1.59] 
[1.60] 
The eikonal equation [1.59]has the following solutions:
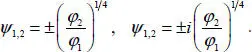
From the transport equation [1.60], we obtain
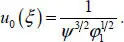
In the first approximation, the general solution of equation [1.56]can be written as follows:
[1.61] 
In expression [1.61], function u 0( ξ ) is “frozen” at either end of the interval (i.e. we can change u 0( ξ ) to u 0(0) or u 0( ξ ) to u 0(1)) for rapidly decaying components).
Using solution [1.61]and boundary conditions [1.57], we obtain the frequency of oscillations:
[1.62] 
Formula [1.62]at φ 1= φ 2= 1 coincides with Bolotin’s formula [1.18]. Thus, the WKBJ method generalizes the DEE method to the problems with variable coefficients.
As it is mentioned in Chen et al . (1991, 1992), the short-wave (high-frequency) asymptotics gives the same results as the DEE approach for domains of simple geometry. At the same time, DEE does not cover the cases of different geometries (circular, elliptical, etc.) or non-self-adjoint problems. The short-wave asymptotics in the form of the Keller–Rubinow approach (Keller and Rubinow 1960) in Chen et al . (1991) allows more ready extension to other geometries and is more aptly generalizable to dissipative boundary conditions. In other words, it gives the possibility to overcome degeneration of the DEE case.
1.8. Conclusion: DEEM, highly recommended
The importance and usefulness of a particular calculation method is determined by its wide application when studying practically important systems and phenomena. From this point of view, the importance of DEEM is not in doubt.
From the very beginning, DEEM was originated by Bolotin for the analysis of overhead power lines (Bolotin et al . 1958).
DEEM was used to obtain estimates for the density of natural frequencies of shallow shell vibrations (Gavrilov 1961b; Bolotin 1963; Stearn 1970; Zhinzher and Khromatov 1971, 1972a, 1972b; Moskalenko 1972, 1975). This is very important during the study of random vibrations of elastic structures (Bolotin 1966; Birger and Panovko 1968; Moskalenko 1968; Bolotin 1984; Elishakoff et al . 1994).
The influence of the magnetic field on the distribution of plate and shell vibration frequencies was studied in Bagdasaryan (1986), Koreshkova and Khromatov (2009), Golubeva et al . (2013) and Khromatov and Golubeva (2013).
A lot of research devoted to the problems of aeroelastic stability and supersonic flutter can be mentioned (Zhinzher 1983; Zhinzher and Kadarmetov 1984, 1986; Dubovskikh et al . 1996).
We also mention the optimal control problem for continuous systems (Andrianov and Iskra 1991).
DEEM and its generalizations are important particular cases of high-frequency asymptotics. The effectiveness of this method for analyzing the main types of plates and shells used in engineering practices has been proven through experience. The main advantage of DEEM consists of its simplicity and good compatibility with variational approaches.
Naturally, DEEM is not a panacea. For example, when considering a mixed boundary value problem with many points of change in the boundary conditions, the method based on the homotopy parameter (Andrianov et al . 2014) seems more suitable.
Nevertheless, in general, we hope that our review has convinced researchers that DEEM and its generalizations occupied an honorable place in the arsenal of analytical methods for solving the dynamics and stability problems of thin-walled structures.
Several years ago, Professor I. Elishakoff pointed out that it would be useful to prepare a new review of Bolotin’s method, since his previous review on this topic was written in 1976. We are grateful to him for this idea.
CONFLICTS OF INTEREST. –The authors declare no conflict of interest.
Professor Elishakoff enjoys historiography of science and his historical research is read with great interest. Bubnov or Galerkin? Timoshenko or Ehrenfest? The chicken or the egg?
Читать дальше

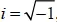 , 0 < ε ≪ 1. In the DEE method, ε = 1/ λ , where λ is the nondimensional frequency. As a result, the construction of the asymptotics can be reduced to solving the eikonal and transport equations (Birger and Panovko 1968). However, short-wave (high-frequency) asymptotics can be treated as a multiscale approach (Maslov and Fedoryuk 1981).
, 0 < ε ≪ 1. In the DEE method, ε = 1/ λ , where λ is the nondimensional frequency. As a result, the construction of the asymptotics can be reduced to solving the eikonal and transport equations (Birger and Panovko 1968). However, short-wave (high-frequency) asymptotics can be treated as a multiscale approach (Maslov and Fedoryuk 1981).


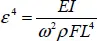 ,
, 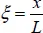 .
.