Stefan Uhlig - Der natürliche Klimawandel

Heute, d.h. in der gegenwärtigen Warmzeit des sogenannten Holozäns, kommt die aktuelle Umlaufbahn der Erde um die Sonne nahezu einer Kreisbahn gleich. D.h. ihre Exzentrizität ist sehr klein und hat den Wert 0,017. Voraussichtlich in knapp weniger als 30.000 Jahren wird die Exzentrizität wieder ihr Minimum erreichen mit einem Wert kleiner als 0,003 ( Abb. 8und Abb. 11). Ein perfekter Kreis hat den Wert 0 und Ellipsen Werte größer 0, aber kleiner 1. Erst wenn die Ellipse zu einer Geraden wird, hat diese dann den Wert von 1. Der aktuelle Abstand zwischen Erde und Sonne, bei sehr kleiner heutiger numerischer Exzentrizität von 0,017, pendelt zwischen einem Minimum von ca. 147,1 Millionen Kilometern, in Sonnennähe, dem sogenannten Perihel, und einem Maximum von rund 152,1 Millionen Kilometern in größter Sonnenferne, dem Aphel. Gegenwärtig sind wir auf der Nordhalbkugel im Winter näher an der Sonne (d.h. im Perihel) als im Sommer (im Aphel), was sich ebenfalls im Laufe der Erdgeschichte ändert. Dazu aber mehr später.

Abb. 8(folgend) : Berechnete numerische Exzentrizitätswerte der Erdumlaufbahn (um die Sonne) 1.000.000 Jahre vor und nach heute. Der aktuelle Wert (im gegenwärtigen Holozän) ist 0,0167 und liegt damit deutlich unter dem Mittelwert von 0,02674 ( blaue Linie). D.h. die aktuelle Umlaufbahn der Erde um die Sonne kommt einer Kreisbahn sehr nahe. Kalt- und Warmzeiten auf der Erde korrelieren deutlich mit Maxima bzw. Minima der Exzentrizität. Quelle: http://www.geoastro.de/kepler/eccentricity1.html(s. auch Abb. 11).

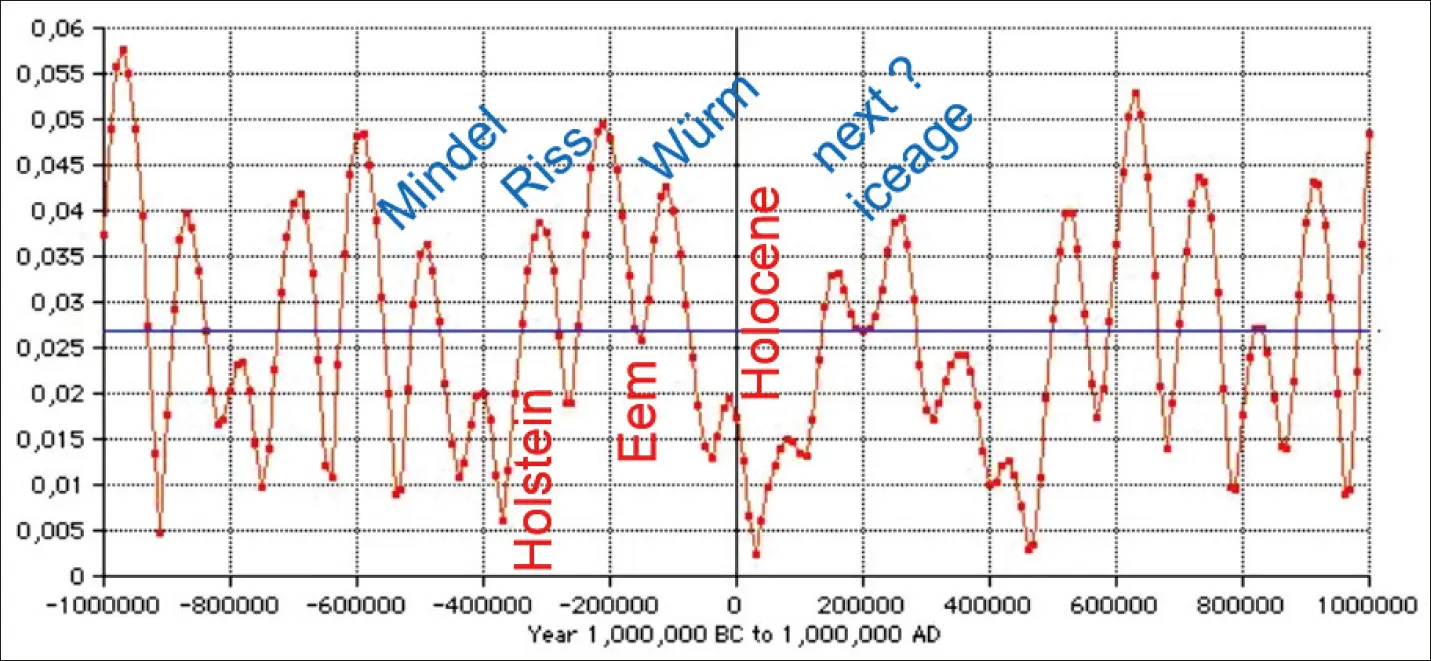
Abb. 8

Dies sind immerhin 5 Millionen EntfernungskilometerDifferenz, bzw. ca. 3 % bzgl. der mittleren Entfernung Erde-Sonne – nur um sich die Dimension dieser astronomischen Variablen vorzustellen. Bei zunehmender Exzentrizität vergrößert sich der Abstand Sonne-Erde im Aphel (Sonnenferne). D.h., die Entfernung Erde-Sonne ist im Aphel (Sonnenferne) bei kleiner Exzentrizität (heute ca. 0,017) deutlich geringer ist als bei großer Exzentrizität (bis zu 0,06 während den letzten Eiszeiten). Bei nur gering größerem Ellipsenradius im Aphel (Sonnenferne) bei zunehmender Exzentrizität wird der Abstand Erde-Sonne entsprechend größer und die Strahlungsintensität der Sonne geringer. Hierbei muss das Abstandsquadratgesetz berücksichtigt werden, das besagt, dass die Strahlungsintensität einer punktförmigen Strahlungsquelle (wie die Sonne) proportional zum Quadrat des Abstandsvon der Strahlungsquelle (hier die Sonne) kleiner wird. Dies heißt, dass bei größer werdender Entfernung von der Sonne die Intensität der Strahlung in Abhängigkeit der linearen Differenzlänge zum Quadrat abnimmt. Das hört sich alles recht kompliziert an, ist mathematisch aber einfach fassbar und berechenbar.

Abb. 9(folgend ): Darstellung der 3 astrophysikalischen Milankovitch-Zyklen; 9-A: Änderung der mehr oder weniger elliptischen Umlaufbahn der Erde um die Sonne (Exzentrizität) mit einer Zyklizität von ca. 100-110.000 Jahren; 9-B: zyklische Änderung der Neigung der Erdachse (Ekliptikschiefe), die im Laufe von ca. 41.000 Jahren variiert zwischen 22,1° und 24,5°; 9-C: Darstellung des Taumelns der Erdachse (Präzession) in Zyklen von 19.000 bis 23.000 Jahren. Quelle: TARBUCK et al. (2005).

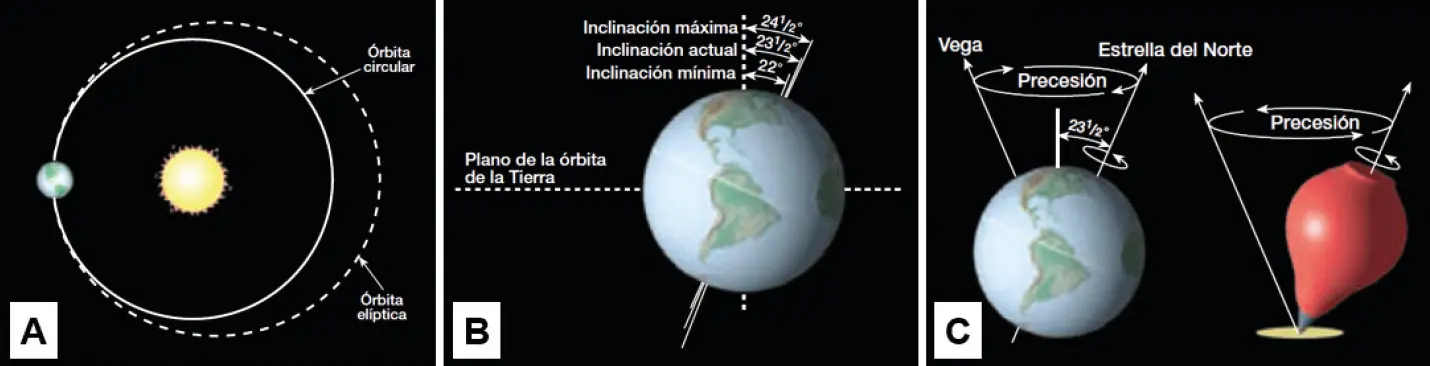
Abb. 9

Bei geringer Sonnenferne im Aphel (max. Sonnenferne), wie in der heutigen Warmzeit des Holozäns, ist die Strahlungsintensität der Sonne zum Quadrat des Entfernungsunterschiedes größer als bei größerer Sonnenferne im Aphel während den letzten Eiszeiten bei größeren Exzentrizitätswerten von bis zu 0,06 (d.h. weniger kreisförmige Umlaufbahn der Erde). Eine relativ größere Exzentrizität, führt letztendlich zu größeren Temperaturunterschieden zwischen Winter und Sommer auf beiden Erdhalbkugeln, da zwischen minimaler (Perihel-) und maximaler (Aphel-) Sonnenentfernungs-Position der Erde 6 Monate (½ Jahr) vergehen. Dies ist besonders relevant für die höheren geographischen Breiten, wo sich die Unterschiede der Sonneneinstrahlung (bzw. Oberflächentemperatur) zwischen Sommer und Winter stärker auswirken. Unter der Annahme, dass der mittlere Abstand Erde–Sonne (149,6 Millionen Kilometer) gleich bliebe, würde bei einer Exzentrizität von 0,06 die Sonnen-nahe Entfernung (im Perihel) ca. 140,6 Millionen Kilometer betragen und im Aphel (max. Sonnenferne) ca. 158,6 Millionen Kilometer. Die Differenz wären dann 18 Millionen Kilometer, bzw. 12 % der mittleren Entfernung.

Die Exzentrizität ändert sich nicht nur in ca. 100.000-110.000 Jahre andauernden Zyklen, wie sie von Milan Milankovitch erkannt wurden. Neuere geowissenschaftliche Untersuchungen bestätigen inzwischen auch einen weiteren Zyklus von ca. 405.000-413.000 Jahre, der sich über Hunderte von Jahrmillionen zurückverfolgen lässt (z.B. KENT et al. 2018). Dazu kommen noch die negativen bzw. positiven Einwirkungen auf die Temperaturentwicklung der Erdatmosphäre und der Ozeane der nächsten beiden, im Folgenden beschriebenen, sich überlagernden Milankovitch-Zyklen.

In einem Zyklus von ca. 41.000 Jahrenvariiert außerdem der Neigungswinkel der Erdachse ( Ekliptikschiefe) zwischen 22,1° und 24,5° ( Abb. 9-B). Der Neigungswinkel, bzw. die geographische Lage der sogenannten Wendekreise südlich und nördlich des Äquators, werden in den Schulatlanten mit 23,5° angegeben. Zurzeit beträgt der Neigungswinkel 23,43684° und verringert sich monatlich um ca. 0,00001°. Bei größerer Ekliptikschiefe (Neigung nahe 24,5°) sind die Temperaturunterschiede (d.h. die Sonneneinstrahlung) zwischen Sommer und Winter auf der Nord- und Südhalbkugel (vor allem in den höheren Breiten) extremer als bei kleiner Ekliptikschiefe (Neigung nahe 22,1°). Dies ist besonders relevant für Klimaänderungen auf der Nordhalbkugel mit höherem Festlandanteil im Vergleich zur Südhalbkugel.

Bei geringer Erdachsenneigung (Ekliptikschiefe) sind die Winter in den höheren Breiten weniger streng. Jedoch können Gletscher größere Schneemassen akkumulieren, da die Verdunstung über dem Meer höher ist und damit mehr Niederschlag fallen kann, bzw. Schnee, wenn die Temperaturen unter dem Gefrierpunkt liegen. In den Sommern wird dagegen die Ablation (das Abschmelzen von Eis und Schnee) durch die geringere Sonneneinstrahlung und die damit im Mittel niedrigeren Temperaturen vermindert. D.h. bei geringer Achsneigung sind die Voraussetzungen für die Bildung von kontinentalen Eisschilden insgesamt günstiger als bei hoher Achsneigung. Tatsächlich liegen die Kaltzeiten des Pleistozäns (der letzten 2,5 Millionen Jahre) meist in Phasen, für die eine geringe Neigung der Erdachse berechnet wurde, während die Warmzeiten mit Phasen hoher Achsneigung korrelieren. Nimmt man bei Abb. 4noch das Marine Isotopen-MIS- Stadium 22 hinzu, so beträgt die dabei erfasste Zeitspanne rund 900.000 Jahre. Entsprechend dauert eine einzelne MIS-Phase ca. 40.900 Jahre, was dem Zyklus der Ekliptikschiefe entspricht. Dies deutet darauf hin, dass die periodischen Änderungen der Ekliptikschiefe in den Marinen Isotopen-Stadien, als Ausdruck der Temperaturentwicklung durch die „proxy“- δ 18O-Indexwerte, wesentlich den Takt angeben.

Hinzu kommt, dass sich ebenfalls die Präzessionder Erdachse in einem Zyklus von ca. 19.000-23.000 Jahrenändert. Mit Präzession ist das Wackeln (Trudeln oder Taumeln) der Erdachse um die Senkrechte der Erdumlaufbahn gemeint ( Abb. 9-C). Mit der Präzessionsbewegung, bei der die Erdachse um die Senkrechte zur Erdbahn kreist, d.h. sie rotiert um den Pol, ändern sich langsam die jahreszeitlichen Positionen der Erde auf der Bahn um die Sonne. Damit ändert sich das Datum von Aphel (max. Sonnenferne, heute max. 152,1 Millionen Kilometer Entfernung Erde–Sonne) und Perihel (max. Sonnennähe, heute min. 147,1 Millionen Kilometer Entfernung Erde–Sonne). Das Wandern der Sonnen-fernen Perihel-Position, bzw. Sonnen-nahen Aphel-Position, entlang der Umlaufbahn der Erde, ist eine Folge der Präzessionsbewegung der rotierenden Erdkugel, die an den Polen leicht abgeplatteter (flacher) ist als am Äquator. Der Erddurchmesser beträgt am Äquator ca. 12.756 km und an den Polen ca. 12.713 km. Die Gravitationskräfte der Sonne, des Mondes und deutlich schwächer die der Nachbarplaneten, wirken auf die schräg stehende Kreiselbewegung der Erde ein. Vergleicht man die Entwicklungen der Temperatur und der Sonneneinstrahlungsenergie der letzten beiden Eiszeiten (Würm und Riss), quasi höher aufgelöst wie in Abb. 10, so erkennt man deutlich den „kleinteiligen“ Rhythmus des Zyklus der Präzession (11 Zyklen in rund 250.000 Jahren).