Beispiele für Merkmalsausprägungen in der Statistik
Das Alter x nimmt bei Person i den Wert x i= 21 Jahre an. Oder: Der Umsatz eines Unternehmens liegt in der Größenklasse zwischen 150.000 und 200.000 €.
Das Ziel der Statistik ist es, Aussagen über „Massen“ in Bezug auf Merkmale (Variablen) zu machen und zu prüfen, ob derartige Feststellungen, wenn sie aufgrund einer Stichprobe gewonnen wurden, verallgemeinerungsfähigsind. Diese Massen sind hinsichtlich sachlicher, räumlicher und zeitlicher Kriterien sinnvoll gebildete Gesamtheiten.

Verständnisfragen
Haben Sie alles verstanden? Mit den folgenden Fragen können Sie das Gelernte schnell prüfen:
Die Statistik ist die Lehre der Methode zur_______________ und ________________ von zahlenmäßigen Informationen über die Wirklichkeit.
| 2 |
Was untersuchen StatistikerInnen nicht? |
| □ |
Merkmale |
| □ |
Beschreibung einer einzelnen Einheit |
| □ |
statistische Masse (Gesamtheit) |
| 3 |
Was ist kein Merkmal? |
| □ |
Alter |
| □ |
Einkommen |
| □ |
eine einzelne Person P |
| 4 |
Wo verfährt man nach dem Zufallsprinzip? Bei der … |
| □ |
Auswahl der Einheiten der Grundgesamtheit im Falle einer Stichprobe |
| □ |
Befragung einer wie immer bestimmten Teilgesamtheit (z. B. der zufällig anwesenden Hörer einer Vorlesung) |

Die Lösungen finden Sie online unter www.uvk-lucius.de/brueckenkurse
| 2 |
Gegenstände der Statistik |
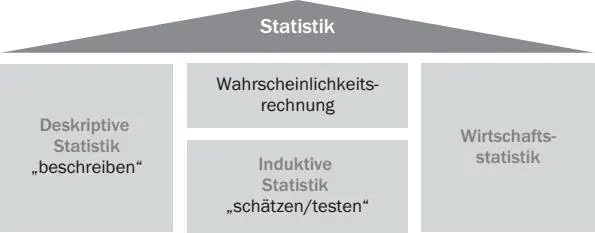
Abb. 1: Die Statistik im Überblick
Die Statistik lässt sich in
| ■ |
die Beschreibende bzw. Deskriptiveund |
| ■ |
die Schließende bzw. Induktive Statistik |
unterscheiden. An einigen Hochschulen wird auch noch Wirtschaftsstatistikgelehrt.
Deskriptive Statistik
Bei der Deskriptiven Statistik geht es um die Gewinnung aussagekräftiger Maßzahlen, wie z. B.
| ■ |
Mittelwerte, |
| ■ |
Streuungsmaße, |
| ■ |
Indexzahlen, |
| ■ |
Korrelationskoeffizienten usw. |
Diese Maßzahlen helfen dabei, einen Datensatz sinnvoll zu beschreibenund zu charakterisieren. Mittelwerte kennzeichnen die Größenordnung oder das Niveau, in der bzw. auf dem sich die einzelnen Werte bewegen.
Beispiel für Mittelwerte
Ein Mittelwert 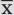 beantwortet die Frage, ob aktuell die Preise für Laptops „im Schnitt“ bei 500 Euro liegen.
beantwortet die Frage, ob aktuell die Preise für Laptops „im Schnitt“ bei 500 Euro liegen.
Da es in der Regel Abweichungen nach oben oder unten gibt, sollte nicht nur ein Mittelwert, sondern auch die Streuunggemessen werden. Dabei hilft die Varianz 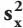 . Sie zeigt die Unterschiedlichkeit der erhobenen Merkmalsausprägungen (Werte) für eine Variable x an und damit die Homogenität einer Masse (Gesamtheit) bezüglich x. Eine Streuung liegt bezogen auf das obige Beispiel vor, wenn es auch Laptops gibt, die günstiger oder auch teurer als 500 € angeboten werden.
. Sie zeigt die Unterschiedlichkeit der erhobenen Merkmalsausprägungen (Werte) für eine Variable x an und damit die Homogenität einer Masse (Gesamtheit) bezüglich x. Eine Streuung liegt bezogen auf das obige Beispiel vor, wenn es auch Laptops gibt, die günstiger oder auch teurer als 500 € angeboten werden.
In der Deskriptiven Statistik spielt es keine Rolle, ob die Daten für die Berechnung einer Maßzahl (wie z. B. der oben genannte Mittelwert 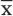 oder die Varianz
oder die Varianz 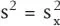 ) aus einer Stichprobe (Zufallsauswahl), einer nichtzufälligen Teilerhebung oder aus einer Vollerhebung stammen.
) aus einer Stichprobe (Zufallsauswahl), einer nichtzufälligen Teilerhebung oder aus einer Vollerhebung stammen.
Statistiker sprechen von einer Vollerhebung, wenn die gesamte Grundgesamtheit untersucht wird. Das ist zum Beispiel der Fall, wenn ohne Ausnahme alle Absolventen eines Jahrgangs zu einem Thema befragt werden. Eine Teilerhebung– insbesondere wenn die Einheiten nach dem Zufallsprinzip ausgewählt wurden – liegt vor, wenn lediglich eine Stichprobeaus der Grundgesamtheit befragt wird, also zum Beispiel nur 25 von 1.000 Absolventen befragt werden.
Im Zusammenhang mit Stichproben ist es üblich, griechische Buchstaben zu verwenden, wie zum Beispiel μ oder σ; lassen Sie sich davon nicht abschrecken.
Aber berücksichtigen Sie im Hinblick auf die Induktive Statistik das Folgende: In der Induktiven Statistik müssen Sie durch Symbole unterscheiden, ob sich etwas auf die Grundgesamtheit oder auf die Stichprobe bezieht. Um hier Klarheit zu schaffen verwenden Statistiker
| ■ |
lateinische Buchstaben (z. B. Standardabweichung s) wenn es sich um die Stichprobe handelt und |
| ■ |
griechische Buchstaben (Standardabweichung der Grundgesamtheit σ) wenn die Grundgesamtheit gemeint ist. |
Induktive Statistik
Bei der Induktiven Statistikgeht um die Beurteilung einer Maßzahl (etwa 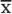 ) im Vergleich zur unbekannten entsprechenden Größe μ xin der Grundgesamtheit, die mit
) im Vergleich zur unbekannten entsprechenden Größe μ xin der Grundgesamtheit, die mit 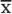 geschätzt wird (μ xwird „Parameter“ genannt). 1Zentrale Gegenstände der Induktiven Statistik sind deshalb das
geschätzt wird (μ xwird „Parameter“ genannt). 1Zentrale Gegenstände der Induktiven Statistik sind deshalb das
| ■ |
Schätzen von Parametern(wie μ bzw. σ 2usw.) aufgrund entsprechender Schätzfunktionen (wie 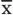 oder s 2, bzw. oder s 2, bzw. 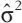 ) mit Werten aus der Stichprobe, und das ) mit Werten aus der Stichprobe, und das |
| ■ |
Testen von Hypothesenüber Parameter. |
Eine Hypotheseist in der Statistik eine Annahme über die Grundgesamtheit, die durch Daten der Stichprobe geprüft werden kann.
Beispiel Prüfung einer Hypothese
Die Wirkung von Schlankheitspillen kann durch zwei Gruppen getestet werden: Die erste Stichprobe ( Experimentgruppe) nimmt die Pillen ein und eine zweite Stichprobe ( Kontrollgruppe) nicht. Nach der Einnahme zeigt sich, dass die durchschnittliche Gewichtsabnahme 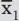 in der Experimentgruppe mit n 1= 10 Personen größer ist als die durchschnittliche Gewichtsabnahme
in der Experimentgruppe mit n 1= 10 Personen größer ist als die durchschnittliche Gewichtsabnahme 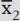 in der Kontrollgruppe mit n 2=10 Personen. In Zahlen lässt sich das wie folgt ausdrücken:
in der Kontrollgruppe mit n 2=10 Personen. In Zahlen lässt sich das wie folgt ausdrücken: 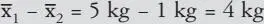 .
.
Читать дальше




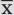 beantwortet die Frage, ob aktuell die Preise für Laptops „im Schnitt“ bei 500 Euro liegen.
beantwortet die Frage, ob aktuell die Preise für Laptops „im Schnitt“ bei 500 Euro liegen.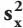 . Sie zeigt die Unterschiedlichkeit der erhobenen Merkmalsausprägungen (Werte) für eine Variable x an und damit die Homogenität einer Masse (Gesamtheit) bezüglich x. Eine Streuung liegt bezogen auf das obige Beispiel vor, wenn es auch Laptops gibt, die günstiger oder auch teurer als 500 € angeboten werden.
. Sie zeigt die Unterschiedlichkeit der erhobenen Merkmalsausprägungen (Werte) für eine Variable x an und damit die Homogenität einer Masse (Gesamtheit) bezüglich x. Eine Streuung liegt bezogen auf das obige Beispiel vor, wenn es auch Laptops gibt, die günstiger oder auch teurer als 500 € angeboten werden.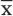 oder die Varianz
oder die Varianz 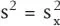 ) aus einer Stichprobe (Zufallsauswahl), einer nichtzufälligen Teilerhebung oder aus einer Vollerhebung stammen.
) aus einer Stichprobe (Zufallsauswahl), einer nichtzufälligen Teilerhebung oder aus einer Vollerhebung stammen.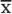 ) im Vergleich zur unbekannten entsprechenden Größe μ xin der Grundgesamtheit, die mit
) im Vergleich zur unbekannten entsprechenden Größe μ xin der Grundgesamtheit, die mit 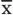 oder s 2, bzw.
oder s 2, bzw. 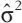 ) mit Werten aus der Stichprobe, und das
) mit Werten aus der Stichprobe, und das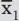 in der Experimentgruppe mit n 1= 10 Personen größer ist als die durchschnittliche Gewichtsabnahme
in der Experimentgruppe mit n 1= 10 Personen größer ist als die durchschnittliche Gewichtsabnahme 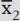 in der Kontrollgruppe mit n 2=10 Personen. In Zahlen lässt sich das wie folgt ausdrücken:
in der Kontrollgruppe mit n 2=10 Personen. In Zahlen lässt sich das wie folgt ausdrücken: 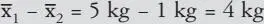 .
.










