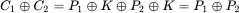
and we see that the key has disappeared from the problem. In this case, the ciphertext does yield some information about the underlying plaintext. Another way to see this is to consider an exhaustive key search. If the pad is only used once, then the attacker has no way to know whether the guessed key is correct or not. But if two messages are in depth, for the correct key, both putative plaintexts must make sense. This provides the attacker with a means to distinguish the correct key from incorrect guesses. The problem only gets worse (or better, from a cryptanalyst's perspective) the more times the key is reused.
Let's consider an example of one‐time pad encryptions that are in depth. Using the same bit encoding as in Table 2.1, suppose we have
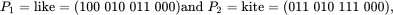
and both are encrypted with the same key 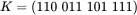 . Then
. Then

and

If Trudy the cryptanalyst knows that the messages are in depth, she immediately sees that the second and fourth letters of 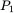 and
and 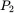 are the same, since the corresponding ciphertext letters are identical. But far more devastating is the fact that Trudy can now guess a putative message
are the same, since the corresponding ciphertext letters are identical. But far more devastating is the fact that Trudy can now guess a putative message 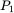 and check her results using
and check her results using 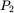 . Suppose that Trudy, who only knows
. Suppose that Trudy, who only knows 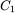 and
and 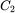 , suspects that
, suspects that  . Then she can find the corresponding putative key
. Then she can find the corresponding putative key

and she can then use this 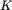 to “decrypt″
to “decrypt″ 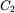 and obtain
and obtain

Since this  does not yield a sensible decryption for
does not yield a sensible decryption for 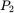 , Trudy can safely assume that her guess for
, Trudy can safely assume that her guess for 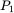 was incorrect. When Trudy eventually guesses that
was incorrect. When Trudy eventually guesses that 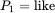 she will obtain the correct key
she will obtain the correct key 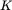 and decrypt to also find that
and decrypt to also find that 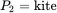 , thereby confirming the correctness of the key and, consequently, the correctness of both decryptions.
, thereby confirming the correctness of the key and, consequently, the correctness of both decryptions.
A classic codebook cipher is, literally, a dictionary‐like book containing (plaintext) words and their corresponding (ciphertext) codewords. To encrypt a word, the cipher clerk would simply look it up in the codebook and replace it with the corresponding codeword. Decryption, using the inverse codebook, is equally straightforward. Below, we briefly discuss the Zimmermann Telegram, which is surely the most infamous use of a codebook cipher in history.
The security of a classic codebook cipher depends primarily on the physical security of the book itself. That is, the book must be protected from capture by the enemy. In addition, statistical attacks analogous to those used to break a simple substitution cipher apply to codebooks, although the amount of data required is much larger. The reason that a statistical attack on a codebook is more difficult is due to the fact that the size of the “alphabet″ is far greater, and consequently, significantly more data must be collected before the statistical information can rise above the noise.
As late as World War II, codebooks were in widespread use. Cryptographers realized that these ciphers were subject to statistical attack, so codebooks needed to be periodically replaced with new codebooks. Since this was an expensive and risky process, techniques were developed to extend the life of a codebook. To accomplish this, a so‐called additive was generally used.
Suppose that for a particular codebook cipher, the codewords are all five‐digit numbers. Then the corresponding additive book would consist of a long list of randomly generated five‐digit numbers. After a plaintext message had been converted to a series of five‐digit codewords, a starting point in the additive book would be selected and beginning from that point, the sequence of five‐digit additives would be added to the codewords to create the ciphertext. To decrypt, the same additive sequence would be subtracted from the ciphertext before looking up the codeword in the codebook. Note that the additive book—as well as the codebook itself—is required to encrypt or decrypt a message.
Often, the starting point in the additive book was selected at random by the sender and sent in the clear (or in a slightly obfuscated form) at the start of the transmission. This additive information was part of the message indicator, or MI. The MI included any non‐secret information needed by the intended recipient to decrypt the message.
If the additive material was only used once, the resulting cipher would be equivalent to a one‐time pad and therefore, provably secure. However, in practice, the additive was reused many times—any messages sent with overlapping additives would have their codewords encrypted with the same key, where the key consists of the codebook and the specific additive sequence. Therefore, any messages with overlapping additive sequences could be used to gather the statistical information needed to attack the underlying codebook. In effect, the additive book dramatically increased the amount of ciphertext required to mount a statistical attack on the codebook, which is precisely the effect that cryptographers had hoped to achieve.
Читать дальше

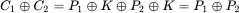
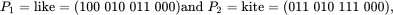
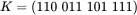 . Then
. Then

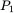 and
and 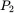 are the same, since the corresponding ciphertext letters are identical. But far more devastating is the fact that Trudy can now guess a putative message
are the same, since the corresponding ciphertext letters are identical. But far more devastating is the fact that Trudy can now guess a putative message 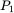 and check her results using
and check her results using 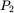 . Suppose that Trudy, who only knows
. Suppose that Trudy, who only knows 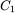 and
and 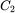 , suspects that
, suspects that  . Then she can find the corresponding putative key
. Then she can find the corresponding putative key
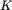 to “decrypt″
to “decrypt″ 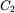 and obtain
and obtain
 does not yield a sensible decryption for
does not yield a sensible decryption for 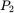 , Trudy can safely assume that her guess for
, Trudy can safely assume that her guess for 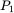 was incorrect. When Trudy eventually guesses that
was incorrect. When Trudy eventually guesses that 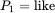 she will obtain the correct key
she will obtain the correct key 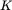 and decrypt to also find that
and decrypt to also find that 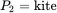 , thereby confirming the correctness of the key and, consequently, the correctness of both decryptions.
, thereby confirming the correctness of the key and, consequently, the correctness of both decryptions.









