Lyapunov exponents are invariant to coordinate transformations and are ordered from largest to smallest [2.29]. They are a measure of the behavior of vectors in a tangent space. As such, these exponents are a measure of stability or instability at each symmetry state. For Lyapunov exponents that are positive, the dynamical system is chaotically unstable [2.29, 2.118], while negative Lyapunov exponents are indicators of a stable dynamical system [2.29]. A Lyapunov exponent with a value of zero may indicate a dissipative, regular [2.35], weakly chaotic [2.73] or intermittent system [2.74], depending on the particulars defining the initial system.
By quantifying the relation between symmetry states and stability via Lyapunov exponents, instability is characterizable as a specific behavior, either deterministically chaotic or not. However, the picture may be more complicated. Slight changes in initial conditions can precipitate chaotic behavior resulting in instability [2.29] even though the initial conditions may be random. Chaotic systems may appear to be random when considering fewer than all possible states in the dynamical system [2.97]. High-dimensional systems may appear to be ordered despite non-convergent random behavior [2.35]. Different kinds of randomness as “noise” may appear to be chaotic in a given dynamical system [2.118]. Care must be taken to discern the behavior of a dynamical system in terms of randomness or chaoticity.
2.2.8 Randomness and Instability
Lyapunov exponents enable the assessment of randomness with respect to instability in a dynamical system [2.74, 2.118, 2.163]. While local unstable behavior on a state-by-state basis may be chaotic, the macro-state instability of valve formation may be inherently random at a global scale. Alternatively, there may be intermittent chaotic or random unstable states [2.74] during the morphogenetic process. Because of this, a test for randomness [2.34] is necessary.
Thus far, our dynamical system model has been analyzed at equilibrium. However, to detect possible random instability, we need to consider the possible non-equilibrium consequences of such behavior in this system. Non-equilibrium may be a long-term phenomenon in contrast to short-term steady-states present in a dynamical system, for example, as time oscillations create Turing effects of diffusion driven instability [2.6]. Toy models have been used to link time intervals over multiple levels enabling the application of equilibrium dynamics to non-equilibrium behavior [2.96]. They have great potential in modeling complicated biological processes [2.2]. Non-equilibrium dynamics can be assessed in terms of constrained information loss or an increase in entropy [2.65].
As entropy increases over longer and longer sequences for a given dynamical system, entropy blocks or sections that define the structure of these sequences do not characterize the entire system. What remains is randomness that is not taken into consideration and given as the source entropy rate 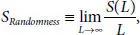 where L is the number of sequence steps [2.26]. One way to test for randomness is to consider the non-deterministic behavior of the valve formation simulated system as a simple renewal process [2.35, 2.74, 2.115]. In a study of morphology and inheritance, Cyclotella meneghiniana offspring cell structure was analyzed for partial renewal with regard to the mother cell and complete renewal in terms of genetic or epigenetic inheritance [2.131], so that valve formation was considered to be a renewal process.
where L is the number of sequence steps [2.26]. One way to test for randomness is to consider the non-deterministic behavior of the valve formation simulated system as a simple renewal process [2.35, 2.74, 2.115]. In a study of morphology and inheritance, Cyclotella meneghiniana offspring cell structure was analyzed for partial renewal with regard to the mother cell and complete renewal in terms of genetic or epigenetic inheritance [2.131], so that valve formation was considered to be a renewal process.
Maximizing the rate of variation in the entropy values during valve formation involves converting Boltzmann entropies of symmetry states to Kolmogorov-Sinai (KS) entropies based on probability [2.97]. KS entropies are time-averaged Shannon entropies over joint probability space [2.147] and are used to construct a PDF as a maximum entropy distribution [2.65, 2.137]. Randomness distributed over a probability distribution involves maximum entropy with regard to a PDF.
Evaluating entropy S using the PDF of associated probabilities involves first derivatives of S as entropy rates [2.26, 2.74] corresponding to bandwidth in the histogram used to determine the PDF [2.137]. For the expected value of the probabilities associated to 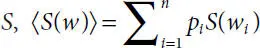 the associated Lyapunov exponents are found via Lagrange multipliers partitioned on the function and given as a maximum entropy probability distribution as
the associated Lyapunov exponents are found via Lagrange multipliers partitioned on the function and given as a maximum entropy probability distribution as 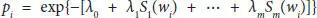 [2.65]. With constraint
[2.65]. With constraint 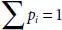 , maximum entropy with respect to Lyapunov exponents is
, maximum entropy with respect to Lyapunov exponents is 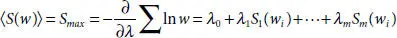 [2.65, 2.67]. Over a probability distribution,
[2.65, 2.67]. Over a probability distribution, 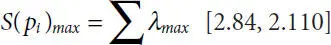 , where
, where 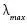 is a positive Lyapunov exponent.
is a positive Lyapunov exponent.
The sum of the positive Lyapunov exponents is a maximization of the possible states of KS entropy, and as such, KS entropy indicates degree of randomness [2.26].
The Lyapunov exponents for KS entropy of a sequence L(t)as a random function over a probability distribution for the αth probability [2.74] are 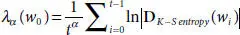 , where DKS entropyis the density matrix of first partial derivatives from KS entropy where the diagonal elements are probability values and t is the time step ofL. Using
, where DKS entropyis the density matrix of first partial derivatives from KS entropy where the diagonal elements are probability values and t is the time step ofL. Using 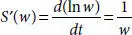 from Boltzmann entropy, Lyapunov exponents from KS entropy become
from Boltzmann entropy, Lyapunov exponents from KS entropy become 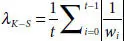 and from Pesin’s identity [2.110],
and from Pesin’s identity [2.110], 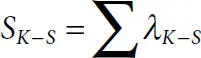 . When SK-S= 0, the rate of prior information loss is equal to the rate of new information created, and stability is evident [2.35]. As A
. When SK-S= 0, the rate of prior information loss is equal to the rate of new information created, and stability is evident [2.35]. As A 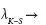
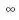 and is no longer a constant when changes in initial conditions approach zero,
and is no longer a constant when changes in initial conditions approach zero, 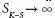 and randomness occurs [2.35]. For a measure of randomness,
and randomness occurs [2.35]. For a measure of randomness, 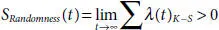 , and
, and 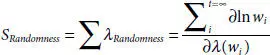 .
.
Читать дальше

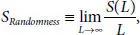 where L is the number of sequence steps [2.26]. One way to test for randomness is to consider the non-deterministic behavior of the valve formation simulated system as a simple renewal process [2.35, 2.74, 2.115]. In a study of morphology and inheritance, Cyclotella meneghiniana offspring cell structure was analyzed for partial renewal with regard to the mother cell and complete renewal in terms of genetic or epigenetic inheritance [2.131], so that valve formation was considered to be a renewal process.
where L is the number of sequence steps [2.26]. One way to test for randomness is to consider the non-deterministic behavior of the valve formation simulated system as a simple renewal process [2.35, 2.74, 2.115]. In a study of morphology and inheritance, Cyclotella meneghiniana offspring cell structure was analyzed for partial renewal with regard to the mother cell and complete renewal in terms of genetic or epigenetic inheritance [2.131], so that valve formation was considered to be a renewal process.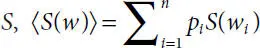 the associated Lyapunov exponents are found via Lagrange multipliers partitioned on the function and given as a maximum entropy probability distribution as
the associated Lyapunov exponents are found via Lagrange multipliers partitioned on the function and given as a maximum entropy probability distribution as 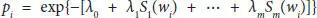 [2.65]. With constraint
[2.65]. With constraint 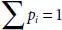 , maximum entropy with respect to Lyapunov exponents is
, maximum entropy with respect to Lyapunov exponents is 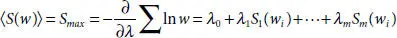 [2.65, 2.67]. Over a probability distribution,
[2.65, 2.67]. Over a probability distribution, 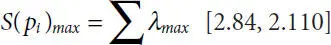 , where
, where 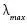 is a positive Lyapunov exponent.
is a positive Lyapunov exponent.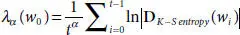 , where DKS entropyis the density matrix of first partial derivatives from KS entropy where the diagonal elements are probability values and t is the time step ofL. Using
, where DKS entropyis the density matrix of first partial derivatives from KS entropy where the diagonal elements are probability values and t is the time step ofL. Using 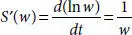 from Boltzmann entropy, Lyapunov exponents from KS entropy become
from Boltzmann entropy, Lyapunov exponents from KS entropy become 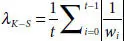 and from Pesin’s identity [2.110],
and from Pesin’s identity [2.110], 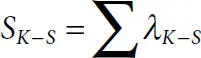 . When SK-S= 0, the rate of prior information loss is equal to the rate of new information created, and stability is evident [2.35]. As A
. When SK-S= 0, the rate of prior information loss is equal to the rate of new information created, and stability is evident [2.35]. As A 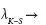
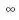 and is no longer a constant when changes in initial conditions approach zero,
and is no longer a constant when changes in initial conditions approach zero, 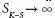 and randomness occurs [2.35]. For a measure of randomness,
and randomness occurs [2.35]. For a measure of randomness, 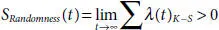 , and
, and 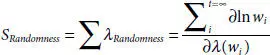 .
.










