Vahid Mirjalili - Python Machine Learning

En secciones anteriores, hemos hablado de los conceptos básicos del aprendizaje automático y de los tres tipos distintos de aprendizaje. En esta sección, hablaremos de las otras partes importantes del sistema de aprendizaje automático que acompañan al algoritmo de aprendizaje. El siguiente diagrama muestra un flujo de trabajo típico para el uso del aprendizaje automático en modelado predictivo, que trataremos en las siguientes subsecciones:

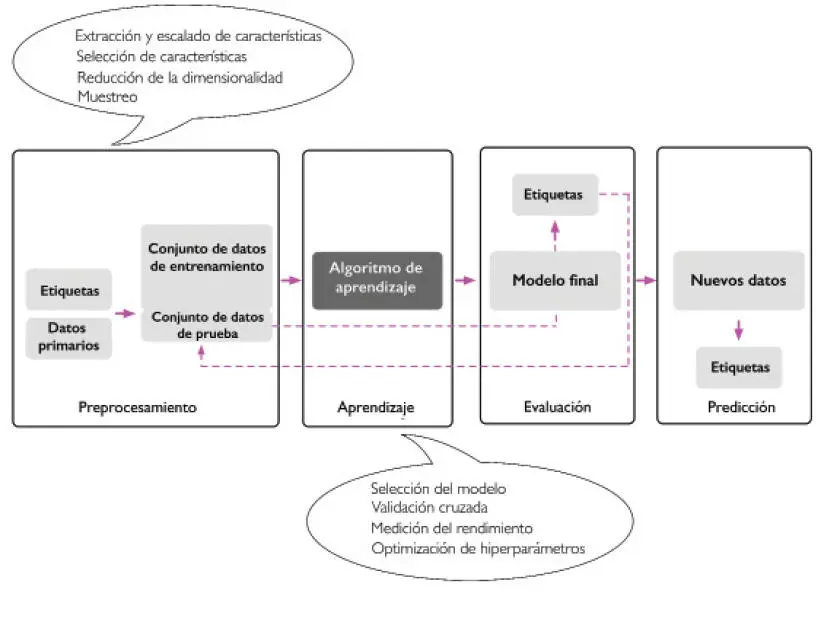
Preprocesamiento: Dar forma a los datos

Vamos a empezar hablando de la hoja de ruta para crear sistemas de aprendizaje automático. No es habitual que los datos primarios se presenten en la forma necesaria para un rendimiento óptimo del algoritmo de aprendizaje. Así, el preprocesamiento de los datos es uno de los pasos más importantes en cualquier aplicación de aprendizaje automático. Si tomamos como ejemplo el conjunto de datos de flores Iris de la sección anterior, podemos pensar en los datos primarios como una serie de imágenes de flores de las cuales queremos extraer características significativas. Estas características útiles pueden ser el color, el tono, la intensidad de las flores, o la altura, la longitud y anchura de la flor. Hay algoritmos de aprendizaje automático que, además, necesitan que las características seleccionadas tengan el mismo tamaño para conseguir un rendimiento óptimo, el cual normalmente se consigue transformando las características en el rango [0, 1] o con una distribución normal estándar con media cero y variación unitaria, como veremos más adelante.

Algunas de las características seleccionadas pueden estar altamente relacionadas y, por tanto, pueden ser redundantes hasta un cierto punto. En estos casos, las técnicas de reducción de dimensionalidad son muy útiles para comprimir las características en un subespacio dimensional más pequeño. Reducir la dimensionalidad de nuestro espacio de características tiene la ventaja de que se requiere menos espacio de almacenamiento y el algoritmo de aprendizaje funciona mucho más rápido. En algunos casos, la reducción de dimensionalidad también puede mejorar el rendimiento predictivo de un modelo si el conjunto de datos contiene un gran número de características irrelevantes (o ruido), es decir, si el conjunto de datos tiene una relación baja entre señal y ruido.

Para determinar si nuestro algoritmo de aprendizaje automático no solo funciona bien en el conjunto de entrenamiento sino que también se generaliza en datos nuevos, también nos interesa dividir de forma aleatoria el conjunto de datos en un conjunto de prueba y de entrenamiento individual. Utilizamos el conjunto de entrenamiento para entrenar y optimizar nuestro modelo de aprendizaje automático, al tiempo que mantenemos el conjunto de prueba hasta el final para evaluar el modelo final.

Entrenar y seleccionar un modelo predictivo

Como veremos en capítulos próximos, se han desarrollado diferentes tipos de algoritmos de aprendizaje automático para resolver distintas tareas problemáticas. Un punto importante que se puede resumir de los famosos teoremas de No hay almuerzo gratis de David Wolpert es que no podemos aprender «gratis». Algunas publicaciones más importantes son The Lack of A Priori Distinctions Between Learning Algorithms [La falta de distinciones a priori entre los algoritmos de aprendizaje], D. H. Wolpert (1996); No free lunch theorems for optimization [Teoremas de no hay almuerzo gratis para la optimización], D. H. Wolpert y W.G. Macready (1997). Intuitivamente, podemos relacionar este concepto con la popular frase: «Si tu única herramienta es un martillo, tiendes a tratar cada problema como si fuera un clavo» (Abraham Maslow, 1966). Por ejemplo, cada algoritmo de clasificación tiene sus sesgos inherentes, y ninguna clasificación individual es superior si no hacemos suposiciones sobre la tarea. En la práctica, resulta esencial comparar como mínimo un puñado de algoritmos distintos para entrenar y seleccionar el mejor modelo de rendimiento. Pero antes de comparar los diferentes modelos, debemos decidir una unidad para medir el rendimiento. Una unidad de medida que se utiliza con frecuencia es la precisión de la clasificación, que se define como la proporción de instancias clasificadas correctamente.

Una cuestión legítima que podemos preguntarnos es: «¿Cómo podemos saber qué modelo funciona bien en el conjunto de datos final y los datos reales si no utilizamos este conjunto de prueba para la selección del modelo, pero sí lo mantenemos para la evolución del modelo final?». Para abordar el problema incluido en esta cuestión, se pueden utilizar diferentes técnicas de validación cruzada, donde el conjunto de datos de entrenamiento se divide en subconjuntos de validación y entrenamiento para estimar el rendimiento de generalización del modelo. Al final, no podemos esperar que los parámetros predeterminados de los diferentes algoritmos de aprendizaje proporcionados por las librerías de los programas sean óptimos para nuestra tarea problemática concreta. Por lo tanto, utilizaremos a menudo técnicas de optimización de hiperparámetros que nos ayudarán, en próximos capítulos, a afinar el rendimiento de nuestro modelo. Intuitivamente, podemos pensar en dichos hiperparámetros como parámetros que no se aprenden de los datos sino que representan los botones de un modelo que podemos girar para mejorar su rendimiento. Todo esto quedará más claro en capítulos posteriores, donde veremos ejemplos reales.

Evaluar modelos y predecir instancias de datos no vistos

Después de haber seleccionado un modelo instalado en el conjunto de datos de entrenamiento, podemos utilizar el conjunto de datos de prueba para estimar cómo funciona con los datos no vistos para estimar el error de generalización. Si su rendimiento nos satisface, ya podemos utilizar este modelo para predecir nuevos y futuros datos. Es importante observar que los parámetros para los procedimientos mencionados anteriormente, como el escalado de características y la reducción de dimensionalidad, solo pueden obtenerse a partir de conjuntos de datos de entrenamiento, y que los mismos parámetros vuelven a aplicarse más tarde para transformar el conjunto de datos de prueba, así como cualquier nueva muestra de datos. De otro modo, el rendimiento medido en los datos de prueba puede ser excesivamente optimista.

Utilizar Python para el aprendizaje automático

Python es uno de los lenguajes de programación más populares para la ciencia de datos y, por ello, cuenta con un elevado número de útiles librerías complementarias desarrolladas por sus excelentes desarrolladores y su comunidad de código abierto.

Aunque el rendimiento de los lenguajes interpretados –como Python– para tareas de cálculo intensivo es inferior al de los lenguajes de bajo nivel, se han desarrollado librerías como NumPy y SciPy sobre implementaciones de C y Fortran de capa inferior para operaciones rápidas y vectorizadas en matrices multidimensionales.

Para tareas de programación de aprendizaje automático, haremos referencia sobre todo a la librería scikit-learn, que actualmente es una de las librerías de aprendizaje automático de código abierto más popular y accesible.

Instalar Python y sus paquetes desde el Python Package Index

Python está disponible para los tres sistemas operativos principales –Microsoft Windows, macOS y Linux– y tanto el instalador como la documentación se pueden descargar desde el sitio web oficial de Python: https://www.python.org.

Este libro está escrito para Python versión 3.5.2 o posterior, y es recomendable que utilices la versión más reciente de Python 3 que esté disponible actualmente, aunque la mayoría de los ejemplos de código también son compatibles con Python 2.7.13 o superior. Si decides utilizar Python 2.7 para ejecutar los ejemplos de código, asegúrate de que conoces las diferencias principales entre ambas versiones. Puedes consultar un buen resumen de las diferencias entre Python 3.5 y 2.7 en https://wiki.python.org/moin/Python2orPython3.