Un conocido ejemplo de aprendizaje reforzado es un motor de ajedrez. Aquí, el agente elige entre una serie de movimientos según el estado del tablero (el entorno), y la recompensa se puede definir como «ganas» o «pierdes» al final del juego:
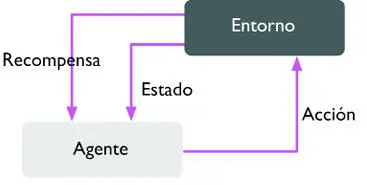
Existen diferentes subtipos de aprendizaje reforzado. Sin embargo, un esquema general es que el agente en aprendizaje reforzado intenta maximizar la recompensa mediante una serie de interacciones con el entorno. Cada estado puede estar asociado a una recompensa positiva o negativa, y una recompensa se puede definir como el logro de un objetivo general (como ganar o perder una partida de ajedrez). Por ejemplo, en ajedrez, el resultado de cada movimiento podría ser un estado distinto del entorno. Para explorar un poco más el ejemplo del ajedrez, pensemos en ciertas jugadas del tablero asociadas a un evento positivo (por ejemplo, eliminar una pieza del contrincante o amenazar a la reina). Sin embargo, otras jugadas están asociadas a un evento negativo (como perder una pieza para el contrincante en el siguiente turno). Ahora, no todos los turnos dan como resultado la eliminación de una pieza del tablero, y el aprendizaje reforzado se centra en aprender las series de pasos maximizando una recompensa basada en el feedback inmediato y diferido.
Aunque esta sección ofrece una visión básica del aprendizaje reforzado, ten en cuenta que las aplicaciones de este tipo de aprendizaje están fuera del alcance de este libro, que prioriza la clasificación, el análisis de regresión y el agrupamiento.
Descubrir estructuras ocultas con el aprendizaje sin supervisión
En el aprendizaje supervisado, cuando entrenamos nuestro modelo sabemos la respuesta correcta de antemano, y en el reforzado definimos una medida de recompensa para acciones concretas mediante el agente. Sin embargo, en el aprendizaje sin supervisión tratamos con datos sin etiquetar o datos de estructura desconocida. Con las técnicas de aprendizaje sin supervisión, podemos explorar la estructura de nuestros datos para extraer información significativa sin la ayuda de una variable de resultado conocida o una función de recompensa.
Encontrar subgrupos con el agrupamiento
El agrupamiento es una técnica exploratoria de análisis de datos que nos permite organizar un montón de información en subgrupos significativos (clústers) sin tener ningún conocimiento previo de los miembros del grupo. Cada clúster que surge durante el análisis define un grupo de objetos que comparten un cierto grado de semejanza pero difieren de los objetos de otros clústers, razón por la cual el agrupamiento también se denomina a veces clasificación sin supervisión. El agrupamiento es una excelente técnica para estructurar información y derivar relaciones significativas de los datos. Por ejemplo, permite a los vendedores descubrir grupos de clientes basados en sus intereses, con el fin de desarrollar programas de marketing exclusivos.
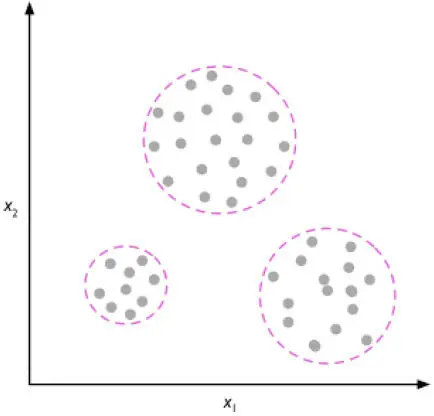
La siguiente figura muestra cómo se puede aplicar el agrupamiento para organizar datos sin etiquetar en tres grupos distintos, basados en la similitud de sus características 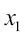 y
y 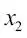 :
:
Reducción de dimensionalidad para comprimir datos
Otro subcampo del aprendizaje sin supervisión es la reducción de dimensionalidad. Muchas veces trabajamos con datos de alta dimensionalidad (cada observación muestra un elevado número de medidas), lo cual puede suponer un reto para el espacio de almacenamiento limitado y el rendimiento computacional de los algoritmos del aprendizaje automático. La reducción de dimensionalidad sin supervisión es un enfoque utilizado con frecuencia en el preprocesamiento de características para eliminar ruido de los datos; también puede degradar el rendimiento predictivo de ciertos algoritmos y comprimir los datos en un subespacio dimensional más pequeño, manteniendo la mayor parte de la información importante.
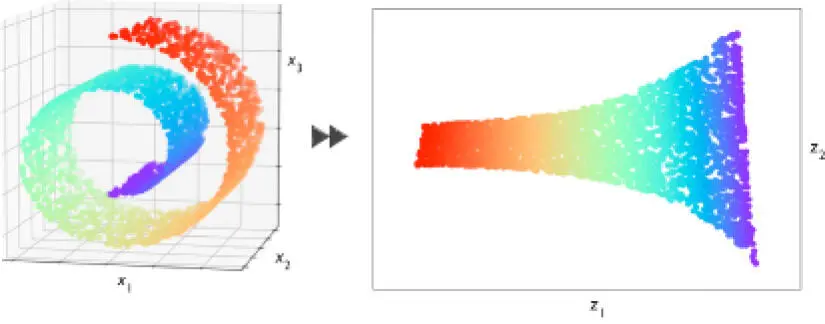
A veces, la reducción de dimensionalidad también puede ser útil para visualizar datos; por ejemplo, un conjunto de características dimensionales pueden ser proyectadas en un espacio de características de una, dos o tres dimensiones para visualizarlas mediante gráficos de dispersión o histogramas 2D o 3D. Las siguientes figuras muestran un ejemplo donde la reducción de dimensionalidad no lineal se ha aplicado para comprimir un brazo de gitano tridimensional en un subespacio con características 2D:
Introducción a la terminología básica y las notaciones
Ahora que ya hemos tratado las tres categorías principales de aprendizaje automático –supervisado, sin supervisión y reforzado–, vamos a echar un vistazo a la terminología básica que utilizaremos en este libro. La tabla siguiente muestra un extracto del conjunto de datos Iris, un ejemplo clásico en el campo del aprendizaje automático. El conjunto de datos Iris contiene las medidas de 150 flores iris de tres especies distintas: Setosa, Versicolor y Virginica. Cada muestra de flor representa una fila de nuestro conjunto de datos y las medidas de la flor en centímetros se almacenan en columnas, que también denominamos características del conjunto de datos:
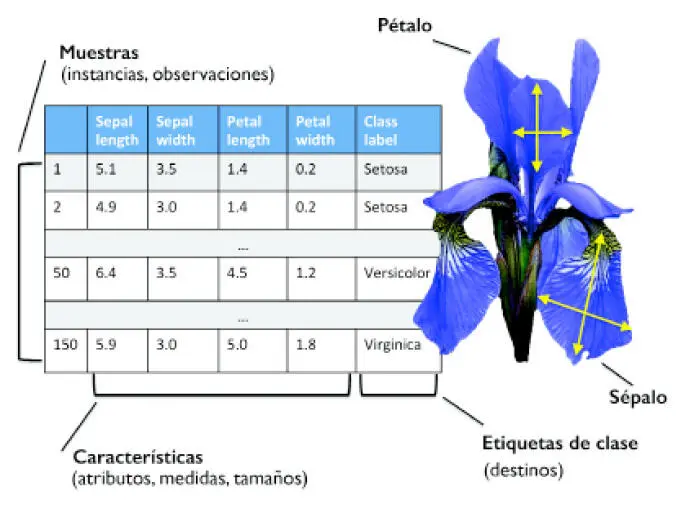
Para que la notación sea simple a la vez que eficiente, utilizaremos algunos de los términos básicos de álgebra lineal. En los siguientes capítulos, utilizaremos una matriz y una notación vectorial para referirnos a nuestros datos. Seguiremos la convención común para representar cada muestra como una fila independiente en una matriz de características X, donde cada característica se almacena en una columna independiente.
Así, el conjunto de datos Iris que contiene 150 muestras y cuatro características también se puede escribir como una matriz 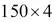
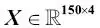 :
:
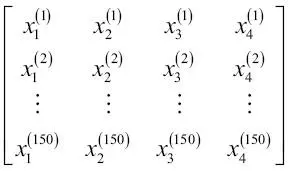
 |
 |
Para el resto del libro, si no se indica de otro modo, utilizaremos el superíndice i para indicar la muestra de entrenamiento i, y el subíndice j para indicar la dimensión j del conjunto de datos de entrenamiento.Utilizamos letras en negrita y minúsculas para referirnos a vectores 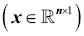 y letras en negrita y mayúsculas para hablar de matrices y letras en negrita y mayúsculas para hablar de matrices 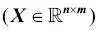 . Para referirnos a elementos individuales en un vector o matriz, escribimos las letras en cursiva ( . Para referirnos a elementos individuales en un vector o matriz, escribimos las letras en cursiva ( 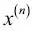 o o 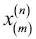 , respectivamente).Por ejemplo, , respectivamente).Por ejemplo, 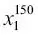 se refiere a la primera dimensión de las 150 muestras de flores, largo de sépalo. Así, cada fila de la matriz de características representa una instancia de flor y puede ser escrita como un vector de fila de cuatro dimensiones se refiere a la primera dimensión de las 150 muestras de flores, largo de sépalo. Así, cada fila de la matriz de características representa una instancia de flor y puede ser escrita como un vector de fila de cuatro dimensiones  : : 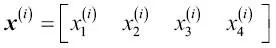 Y cada dimensión de características es un vector de columna de 150 dimensiones Y cada dimensión de características es un vector de columna de 150 dimensiones 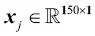 . Por ejemplo: . Por ejemplo: 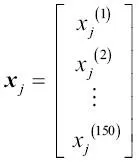 De forma similar, almacenamos las variables de destino (aquí, etiquetas de clase) como un vector de columna de 150 dimensiones: De forma similar, almacenamos las variables de destino (aquí, etiquetas de clase) como un vector de columna de 150 dimensiones:  |
 |
Una hoja de ruta para crear sistemas de aprendizaje automático
Читать дальше


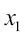 y
y 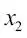 :
:


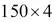
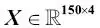 :
: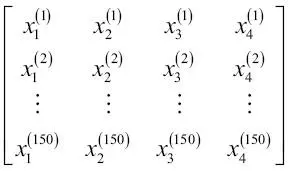


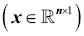 y letras en negrita y mayúsculas para hablar de matrices
y letras en negrita y mayúsculas para hablar de matrices 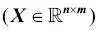 . Para referirnos a elementos individuales en un vector o matriz, escribimos las letras en cursiva (
. Para referirnos a elementos individuales en un vector o matriz, escribimos las letras en cursiva ( 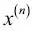 o
o 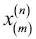 , respectivamente).Por ejemplo,
, respectivamente).Por ejemplo, 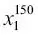 se refiere a la primera dimensión de las 150 muestras de flores, largo de sépalo. Así, cada fila de la matriz de características representa una instancia de flor y puede ser escrita como un vector de fila de cuatro dimensiones
se refiere a la primera dimensión de las 150 muestras de flores, largo de sépalo. Así, cada fila de la matriz de características representa una instancia de flor y puede ser escrita como un vector de fila de cuatro dimensiones  :
: 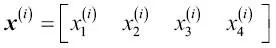 Y cada dimensión de características es un vector de columna de 150 dimensiones
Y cada dimensión de características es un vector de columna de 150 dimensiones 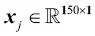 . Por ejemplo:
. Por ejemplo: 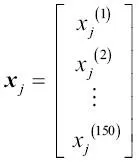 De forma similar, almacenamos las variables de destino (aquí, etiquetas de clase) como un vector de columna de 150 dimensiones:
De forma similar, almacenamos las variables de destino (aquí, etiquetas de clase) como un vector de columna de 150 dimensiones: 












