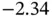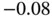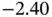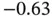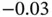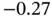Table 1.2Descriptive statistics for the AIDS Blood Transfusion Data: sample size 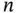 and mean (and standard deviation, SD) for the incubation time (months) by age at infection.
and mean (and standard deviation, SD) for the incubation time (months) by age at infection.
| Age group |
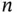 |
Mean (SD) |
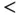 30 years 30 years |
56 |
27.09 (18.28) |
| 30–60 years |
104 |
33.80 (18.95) |
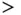 60 years 60 years |
135 |
32.46 (16.74) |
This dataset is used in Chapters 2, 3, 4and 5and can be obtained from AIDS.DTin DTDApackage.
1.4.3 Equipment‐ SRounded Failure Time Data
Companies are often interested in estimating the time to failure of their devices after installation. For doing this, maintenance departments may register events of failure between two specific dates 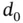 and
and 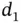 for the units installed in the field. This field lifetime distribution is, however, doubly truncated because of the interval sampling. The Equipment‐
for the units installed in the field. This field lifetime distribution is, however, doubly truncated because of the interval sampling. The Equipment‐ Sdata (Ye and Tang, 2016) concern 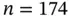 failures of a certain device (details are not given due to confidentiality issues) recorded between 1996 and 2011, a 15 year long observational window. Information on the date of installation and the date of failure, rounded to years, was obtained by digitizing Figure 2 in the referred paper. This dataset is therefore a discrete version of the original data in Ye and Tang (2016). In this example the right‐truncation time
failures of a certain device (details are not given due to confidentiality issues) recorded between 1996 and 2011, a 15 year long observational window. Information on the date of installation and the date of failure, rounded to years, was obtained by digitizing Figure 2 in the referred paper. This dataset is therefore a discrete version of the original data in Ye and Tang (2016). In this example the right‐truncation time  is the number of years between installation and 2011, while the left‐truncation time is just
is the number of years between installation and 2011, while the left‐truncation time is just 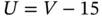 . In Table 1.3the Equipment‐
. In Table 1.3the Equipment‐ Sfailure times are summarized.
The observable range for the Equipment‐ Sfailure times goes from zero to 34 years, which is the maximum observed value for the right‐truncating variable 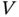 ; hence, estimation of the reliability can only be done conditional on failure within the first 34 years of operation.
; hence, estimation of the reliability can only be done conditional on failure within the first 34 years of operation.
EqSRoundedin the DTDApackage contains this dataset, which is used in Chapter 2.
A classical motivating example of doubly truncated data, introduced by Efron and Petrosian (1999), is found in cosmology when registering the luminosity of quasars. Quasars are observed only if the luminosity lies within a certain interval, bounded at both ends that are determined by detection limits of observation devices, so the data suffer from double truncation. The original dataset studied by Efron and Petrosian (1999) comprises 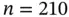 triplets
triplets 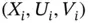 , where
, where 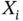 is the luminosity in the log‐scale, obtained from a transformation model based on the redshift and the apparent magnitude of the
is the luminosity in the log‐scale, obtained from a transformation model based on the redshift and the apparent magnitude of the 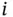 th quasar. See Efron and Petrosian (1999) for further details on the transformation model. Due to experimental constraints, the distribution of each luminosity in the log‐scale is truncated to a known interval
th quasar. See Efron and Petrosian (1999) for further details on the transformation model. Due to experimental constraints, the distribution of each luminosity in the log‐scale is truncated to a known interval 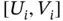 . Specifically, quasars with apparent magnitude above
. Specifically, quasars with apparent magnitude above 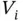 were too dim to yield dependent redshifts, and hence they were excluded from the study. In addition, the lower limit
were too dim to yield dependent redshifts, and hence they were excluded from the study. In addition, the lower limit 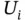 was used to avoid confusion with non‐quasar stellar objects. Some descriptive statistics are provided in Table 1.4.
was used to avoid confusion with non‐quasar stellar objects. Some descriptive statistics are provided in Table 1.4.
Table 1.3Years to failure and number of failing units for the Equipment‐ SRounded Failure Time Data.
| Years: |
0–4 |
5–9 |
10–14 |
15–19 |
20–24 |
25–29 |
30–34 |
| N. units: |
1 |
26 |
26 |
51 |
44 |
14 |
12 |
Table 1.4Descriptive statistics for the Quasar Data. Luminosity in log‐scale ( 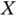 ) and observation interval
) and observation interval 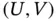 .
.
| Variable |
Min |
Q1 |
Q2 |
Mean |
Q3 |
Max |
| X |
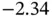 |
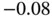 |
0.39 |
0.24 |
0.71 |
2.08 |
| U |
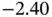 |
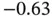 |
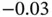 |
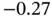 |
0.26 |
0.75 |
| V |
0.15 |
1.78 |
2.10 |
1.95 |
2.36 |
2.58 |
The Quasar Data are used in Chapter 3. This classical example is also included in the DTDApackage (dataset Quasars).
1.4.5 Parkinson's Disease Data
Clark et al. (2011) investigated the association of candidate single nucleotide polymorphisms (SNPs) and age of onset of Parkinson's disease (PD). For this, genomic DNA samples from human blood samples were obtained from the National Institute of Neurological Disorders and Stroke (NINDS) Human Genetics DNA and Cell Line Repository at the Coriell Institute for Medical Research (Camden, New Jersey). More specifically, one aim of the study was to detect association between the rs8192678 PGC‐1a and A10398G SNPs and the risk or age of onset of PD.
Читать дальше

 and mean (and standard deviation, SD) for the incubation time (months) by age at infection.
and mean (and standard deviation, SD) for the incubation time (months) by age at infection.
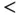 30 years
30 years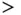 60 years
60 years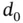 and
and 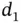 for the units installed in the field. This field lifetime distribution is, however, doubly truncated because of the interval sampling. The Equipment‐
for the units installed in the field. This field lifetime distribution is, however, doubly truncated because of the interval sampling. The Equipment‐ 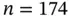 failures of a certain device (details are not given due to confidentiality issues) recorded between 1996 and 2011, a 15 year long observational window. Information on the date of installation and the date of failure, rounded to years, was obtained by digitizing Figure 2 in the referred paper. This dataset is therefore a discrete version of the original data in Ye and Tang (2016). In this example the right‐truncation time
failures of a certain device (details are not given due to confidentiality issues) recorded between 1996 and 2011, a 15 year long observational window. Information on the date of installation and the date of failure, rounded to years, was obtained by digitizing Figure 2 in the referred paper. This dataset is therefore a discrete version of the original data in Ye and Tang (2016). In this example the right‐truncation time  is the number of years between installation and 2011, while the left‐truncation time is just
is the number of years between installation and 2011, while the left‐truncation time is just 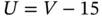 . In Table 1.3the Equipment‐
. In Table 1.3the Equipment‐ 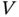 ; hence, estimation of the reliability can only be done conditional on failure within the first 34 years of operation.
; hence, estimation of the reliability can only be done conditional on failure within the first 34 years of operation.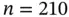 triplets
triplets 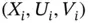 , where
, where 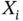 is the luminosity in the log‐scale, obtained from a transformation model based on the redshift and the apparent magnitude of the
is the luminosity in the log‐scale, obtained from a transformation model based on the redshift and the apparent magnitude of the 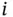 th quasar. See Efron and Petrosian (1999) for further details on the transformation model. Due to experimental constraints, the distribution of each luminosity in the log‐scale is truncated to a known interval
th quasar. See Efron and Petrosian (1999) for further details on the transformation model. Due to experimental constraints, the distribution of each luminosity in the log‐scale is truncated to a known interval 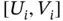 . Specifically, quasars with apparent magnitude above
. Specifically, quasars with apparent magnitude above 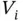 were too dim to yield dependent redshifts, and hence they were excluded from the study. In addition, the lower limit
were too dim to yield dependent redshifts, and hence they were excluded from the study. In addition, the lower limit 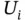 was used to avoid confusion with non‐quasar stellar objects. Some descriptive statistics are provided in Table 1.4.
was used to avoid confusion with non‐quasar stellar objects. Some descriptive statistics are provided in Table 1.4.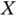 ) and observation interval
) and observation interval 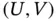 .
.