With interval sampling the variable 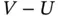 is degenerated at
is degenerated at  . This occurs in other sampling schemes too, in which
. This occurs in other sampling schemes too, in which  and
and 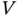 are certain subject‐specific event dates. An illustrative example is given by the Parkinson's Disease Data, see Section 1.4.5, where
are certain subject‐specific event dates. An illustrative example is given by the Parkinson's Disease Data, see Section 1.4.5, where  is the individual age at blood sampling. When
is the individual age at blood sampling. When 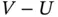 is constant, the couple
is constant, the couple 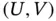 falls on a line, and its joint density does not exist, even when the truncating variables may be continuous.
falls on a line, and its joint density does not exist, even when the truncating variables may be continuous.
In other situations, the truncating variables 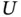 and
and 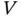 are not linked through the linear equation
are not linked through the linear equation 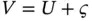 . For example,
. For example, 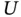 and
and  could represent some random observation limits beyond which the variable of interest
could represent some random observation limits beyond which the variable of interest 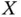 can not be sampled or detected. Situations like this occur for example in Astronomy, as it is illustrated in Section 1.4.4.
can not be sampled or detected. Situations like this occur for example in Astronomy, as it is illustrated in Section 1.4.4.
With random double truncation, both large and small values of 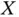 are observed in principle with a relatively small probability. However, the real observational bias for
are observed in principle with a relatively small probability. However, the real observational bias for 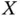 varies from application to application, depending on the joint distribution of
varies from application to application, depending on the joint distribution of 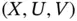 . We will see, for example, that the probability of sampling a value
. We will see, for example, that the probability of sampling a value  , namely
, namely  , may be roughly constant, inducing no observational bias; or that it may be roughly decreasing, indicating the dominance of the right‐truncation bias relative to the left‐truncation bias.
, may be roughly constant, inducing no observational bias; or that it may be roughly decreasing, indicating the dominance of the right‐truncation bias relative to the left‐truncation bias.
Another issue of relevance is that of the identifiability of the distribution of 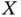 . Intuitively it is clear that with doubly truncated data it is only possible to estimate the distribution of
. Intuitively it is clear that with doubly truncated data it is only possible to estimate the distribution of 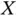 conditional on
conditional on 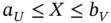 , where
, where 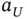 and
and 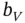 denote respectively the lower and upper endpoints of the supports of
denote respectively the lower and upper endpoints of the supports of 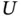 and
and 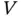 (see Chapter 2for details). This may have important practical consequences, as we will see. On the other hand, in applications with doubly truncated survival data the estimates correspond to the susceptible population for which the terminal event of interest is sure. This is in contrast to the standard analysis of survival times where a portion of the individuals may belong to the so‐called cured fraction , or immunes. This should be taken into account when interpreting the results from the analysis.
(see Chapter 2for details). This may have important practical consequences, as we will see. On the other hand, in applications with doubly truncated survival data the estimates correspond to the susceptible population for which the terminal event of interest is sure. This is in contrast to the standard analysis of survival times where a portion of the individuals may belong to the so‐called cured fraction , or immunes. This should be taken into account when interpreting the results from the analysis.
An important difference of double truncation when compared to one‐sided truncation is that, with doubly truncated data, the NPMLE of the probability distribution has no explicit form. In fact, the NPMLE may be non‐unique and even non‐existing (Xiao and Hudgens, 2019); see Chapter 2. Several iterative algorithms that have been proposed to compute the NPMLE in practice (Efron and Petrosian, 1999; Shen, 2010) will be reviewed in this book, and simulated and real data examples will be analysed with existing libraries of the software R. Semiparametric and parametric alternatives to the NPMLE will be introduced too; these approaches avoid some of the aforementioned potential issues of non‐uniqueness or non‐existence of the NPMLE, also reducing the variance at the price of introducing some bias in estimation. Also, resampling procedures, testing problems, smoothing methods, regression models and multi‐state data analysis under double truncation will be presented.
In this section we introduce the datasets that will be used throughout the book for illustration purposes. All of them suffer from double truncation. These examples are available within the last update of the DTDApackage (Moreira et al., 2021a).
1.4.1 Childhood Cancer Data
The Childhood Cancer Data were gathered from the IPO ( Instituto Português de Oncologia ) of Porto, Portugal, by the RORENO (Registro Oncológico do Norte) service. The information corresponds to all children diagnosed from cancer between 1 January 1999 ( 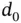 ) and 31 December 2003 (
) and 31 December 2003 ( 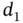 ) in the region of North Portugal, which includes five districts: Porto, Braga, Bragança, Vila Real and Viana do Castelo. The variable of main interest
) in the region of North Portugal, which includes five districts: Porto, Braga, Bragança, Vila Real and Viana do Castelo. The variable of main interest 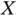 is the age at diagnosis which, by definition of childhood cancer, is supported on the
is the age at diagnosis which, by definition of childhood cancer, is supported on the  interval (time in years). The number of cases was 409. However, for three cases the value of
interval (time in years). The number of cases was 409. However, for three cases the value of 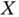 was not available, so we only consider the
was not available, so we only consider the 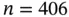 children who report complete information.
children who report complete information.
Читать дальше

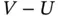 is degenerated at
is degenerated at  . This occurs in other sampling schemes too, in which
. This occurs in other sampling schemes too, in which  and
and 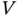 are certain subject‐specific event dates. An illustrative example is given by the Parkinson's Disease Data, see Section 1.4.5, where
are certain subject‐specific event dates. An illustrative example is given by the Parkinson's Disease Data, see Section 1.4.5, where  is the individual age at blood sampling. When
is the individual age at blood sampling. When 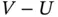 is constant, the couple
is constant, the couple 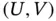 falls on a line, and its joint density does not exist, even when the truncating variables may be continuous.
falls on a line, and its joint density does not exist, even when the truncating variables may be continuous.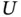 and
and 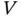 are not linked through the linear equation
are not linked through the linear equation 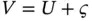 . For example,
. For example, 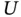 and
and  could represent some random observation limits beyond which the variable of interest
could represent some random observation limits beyond which the variable of interest 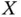 can not be sampled or detected. Situations like this occur for example in Astronomy, as it is illustrated in Section 1.4.4.
can not be sampled or detected. Situations like this occur for example in Astronomy, as it is illustrated in Section 1.4.4.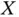 are observed in principle with a relatively small probability. However, the real observational bias for
are observed in principle with a relatively small probability. However, the real observational bias for 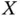 varies from application to application, depending on the joint distribution of
varies from application to application, depending on the joint distribution of 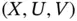 . We will see, for example, that the probability of sampling a value
. We will see, for example, that the probability of sampling a value  , namely
, namely  , may be roughly constant, inducing no observational bias; or that it may be roughly decreasing, indicating the dominance of the right‐truncation bias relative to the left‐truncation bias.
, may be roughly constant, inducing no observational bias; or that it may be roughly decreasing, indicating the dominance of the right‐truncation bias relative to the left‐truncation bias.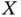 . Intuitively it is clear that with doubly truncated data it is only possible to estimate the distribution of
. Intuitively it is clear that with doubly truncated data it is only possible to estimate the distribution of 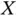 conditional on
conditional on 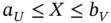 , where
, where 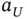 and
and 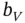 denote respectively the lower and upper endpoints of the supports of
denote respectively the lower and upper endpoints of the supports of 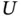 and
and 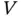 (see Chapter 2for details). This may have important practical consequences, as we will see. On the other hand, in applications with doubly truncated survival data the estimates correspond to the susceptible population for which the terminal event of interest is sure. This is in contrast to the standard analysis of survival times where a portion of the individuals may belong to the so‐called cured fraction , or immunes. This should be taken into account when interpreting the results from the analysis.
(see Chapter 2for details). This may have important practical consequences, as we will see. On the other hand, in applications with doubly truncated survival data the estimates correspond to the susceptible population for which the terminal event of interest is sure. This is in contrast to the standard analysis of survival times where a portion of the individuals may belong to the so‐called cured fraction , or immunes. This should be taken into account when interpreting the results from the analysis.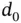 ) and 31 December 2003 (
) and 31 December 2003 ( 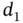 ) in the region of North Portugal, which includes five districts: Porto, Braga, Bragança, Vila Real and Viana do Castelo. The variable of main interest
) in the region of North Portugal, which includes five districts: Porto, Braga, Bragança, Vila Real and Viana do Castelo. The variable of main interest 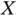 is the age at diagnosis which, by definition of childhood cancer, is supported on the
is the age at diagnosis which, by definition of childhood cancer, is supported on the  interval (time in years). The number of cases was 409. However, for three cases the value of
interval (time in years). The number of cases was 409. However, for three cases the value of 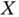 was not available, so we only consider the
was not available, so we only consider the 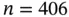 children who report complete information.
children who report complete information.










