Parts of this book were written while the authors were supported by the Grants MTM2017‐89422‐P (MINECO/AEI/FEDER, UE) (first author), UIDB/00013/2020 and UIDP/00013/2020 (second author), and MTM2016‐76969‐P (MINECO/AEI/FEDER, UE) (third author). This is acknowledged.
| May 2021 |
|
Jacobo de Uña‐Álvarez, Carla Moreira and Rosa M. CrujeirasVigo, V. N. Famalicão and Santiago de Compostela |
1 Introduction
1.1 Random Truncation
Random truncation generally refers to a situation in which a number of individuals of the target population cannot be sampled because a certain random event precludes them. When this random event is unrelated to the variables of interest standard statistical methods apply, with the only inconvenience of using a smaller sample size. In many practical cases, however, the truncation event is related to the variables under study, and specific methods to overcome the sampling bias must be considered.
This book is focused on random truncation phenomena that arise (usually, but not only) when sampling time‐to‐event data. That is, the variable of interest is the time 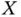 elapsed from a well‐defined origin to another well‐defined end point. In this setting, a truncated sample of
elapsed from a well‐defined origin to another well‐defined end point. In this setting, a truncated sample of 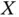 is a set of independent and identically distributed (iid) random variables
is a set of independent and identically distributed (iid) random variables 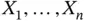 with the conditional distribution of
with the conditional distribution of 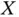 given
given 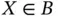 , where
, where 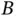 is a random set. Since the truncation event
is a random set. Since the truncation event 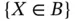 is obviously related to
is obviously related to  , standard statistical methods applied to the truncated sample may be systematically biased. For example, the ordinary empirical cumulative distribution function (ecdf) of
, standard statistical methods applied to the truncated sample may be systematically biased. For example, the ordinary empirical cumulative distribution function (ecdf) of 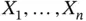 at point
at point 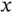 ,
, 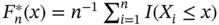 , converges to
, converges to  rather than to the target cumulative distribution function (cdf)
rather than to the target cumulative distribution function (cdf) 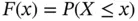 . This problem has received remarkable attention since the seminal paper by Turnbull (1976). Special forms of truncation when sampling time‐to‐event data are reviewed in Sections 1.2and 1.3.
. This problem has received remarkable attention since the seminal paper by Turnbull (1976). Special forms of truncation when sampling time‐to‐event data are reviewed in Sections 1.2and 1.3.
Time‐to‐event data are relevant in fields like Survival Analysis and Reliability Engineering, in which random truncation often occurs. Random truncation is found in Astronomy too, where 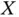 represents the luminosity of an stellar object that is subject to observation limits. Examples from these areas will be introduced and analysed throughout this book.
represents the luminosity of an stellar object that is subject to observation limits. Examples from these areas will be introduced and analysed throughout this book.
1.2 One‐sided Truncation
1.2.1 Left‐truncation
Left‐truncation is a common feature when sampling time‐to‐event data. A left‐truncation time for the target 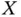 is defined as a random variable
is defined as a random variable 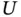 such that
such that 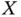 is observed only when
is observed only when 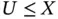 , determining the random set
, determining the random set 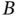 in the previous section.
in the previous section.
Left‐truncation occurs, for example, with cross‐sectional sampling, where the sampled individuals are those being between the origin and the end point at a certain calendar time, which is the cross‐section date (Wang, 1991). That is, the observer arrives at the process at a given date, being allowed to observe the time‐to‐event 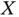 and the left‐truncation time
and the left‐truncation time 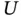 for the individuals 'in progress' by that date. With cross‐sectional sampling, the variable
for the individuals 'in progress' by that date. With cross‐sectional sampling, the variable 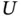 is simply defined as the time from onset to the cross‐section date. This sampling procedure is often applied because it entails relatively little effort to reach a pre‐specified sampling size. In medical research, such a design leads to the sampling of the so‐called prevalent cases: patients already diagnosed from a certain disease of interest who survived beyond the cross‐section date. Clearly, such a sampling design implies an observational bias, in the sense that individuals with longer survival (the
is simply defined as the time from onset to the cross‐section date. This sampling procedure is often applied because it entails relatively little effort to reach a pre‐specified sampling size. In medical research, such a design leads to the sampling of the so‐called prevalent cases: patients already diagnosed from a certain disease of interest who survived beyond the cross‐section date. Clearly, such a sampling design implies an observational bias, in the sense that individuals with longer survival (the 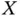 value) will be observed with a relatively large probability. There exist well investigated proposals to overcome such a bias, based on the simple idea of taking the observed left‐truncation times into account to define suitable risk sets. For this purpose, independence between
value) will be observed with a relatively large probability. There exist well investigated proposals to overcome such a bias, based on the simple idea of taking the observed left‐truncation times into account to define suitable risk sets. For this purpose, independence between 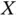 and
and 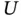 has been traditionally assumed. This independence assumption states that the time‐to‐event distribution remains unchanged along time, being unrelated to the date of onset. A classical example of left‐truncation are the Channing House data, where the age at death is measured for people living in that retirement centre; in this case, the target variable is left‐truncated by the age when entering the residence (Klein and Moeschberger, 2003).
has been traditionally assumed. This independence assumption states that the time‐to‐event distribution remains unchanged along time, being unrelated to the date of onset. A classical example of left‐truncation are the Channing House data, where the age at death is measured for people living in that retirement centre; in this case, the target variable is left‐truncated by the age when entering the residence (Klein and Moeschberger, 2003).
Another feature leading to left‐truncation is the delayed entry into study. This happens when the individuals enter the study only at some random time 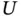 after onset. For example, diagnosis of a certain disease may not be ascertained until the first visit to the hospital. If the 'end‐of‐disease' event occurs before the potential date of visit, the time‐to‐event of such a patient will be never known, with the resulting difficulty in observing relatively small event times. Beyersmann et al. (2012) provide an illustrative example of this issue in the investigation of abortion times.
after onset. For example, diagnosis of a certain disease may not be ascertained until the first visit to the hospital. If the 'end‐of‐disease' event occurs before the potential date of visit, the time‐to‐event of such a patient will be never known, with the resulting difficulty in observing relatively small event times. Beyersmann et al. (2012) provide an illustrative example of this issue in the investigation of abortion times.
Читать дальше

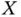 elapsed from a well‐defined origin to another well‐defined end point. In this setting, a truncated sample of
elapsed from a well‐defined origin to another well‐defined end point. In this setting, a truncated sample of 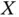 is a set of independent and identically distributed (iid) random variables
is a set of independent and identically distributed (iid) random variables 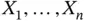 with the conditional distribution of
with the conditional distribution of 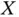 given
given 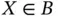 , where
, where 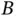 is a random set. Since the truncation event
is a random set. Since the truncation event 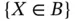 is obviously related to
is obviously related to  , standard statistical methods applied to the truncated sample may be systematically biased. For example, the ordinary empirical cumulative distribution function (ecdf) of
, standard statistical methods applied to the truncated sample may be systematically biased. For example, the ordinary empirical cumulative distribution function (ecdf) of 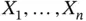 at point
at point 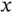 ,
, 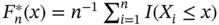 , converges to
, converges to  rather than to the target cumulative distribution function (cdf)
rather than to the target cumulative distribution function (cdf) 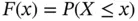 . This problem has received remarkable attention since the seminal paper by Turnbull (1976). Special forms of truncation when sampling time‐to‐event data are reviewed in Sections 1.2and 1.3.
. This problem has received remarkable attention since the seminal paper by Turnbull (1976). Special forms of truncation when sampling time‐to‐event data are reviewed in Sections 1.2and 1.3.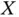 represents the luminosity of an stellar object that is subject to observation limits. Examples from these areas will be introduced and analysed throughout this book.
represents the luminosity of an stellar object that is subject to observation limits. Examples from these areas will be introduced and analysed throughout this book.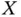 is defined as a random variable
is defined as a random variable 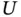 such that
such that 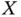 is observed only when
is observed only when 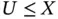 , determining the random set
, determining the random set 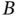 in the previous section.
in the previous section.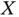 and the left‐truncation time
and the left‐truncation time 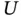 for the individuals 'in progress' by that date. With cross‐sectional sampling, the variable
for the individuals 'in progress' by that date. With cross‐sectional sampling, the variable 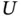 is simply defined as the time from onset to the cross‐section date. This sampling procedure is often applied because it entails relatively little effort to reach a pre‐specified sampling size. In medical research, such a design leads to the sampling of the so‐called prevalent cases: patients already diagnosed from a certain disease of interest who survived beyond the cross‐section date. Clearly, such a sampling design implies an observational bias, in the sense that individuals with longer survival (the
is simply defined as the time from onset to the cross‐section date. This sampling procedure is often applied because it entails relatively little effort to reach a pre‐specified sampling size. In medical research, such a design leads to the sampling of the so‐called prevalent cases: patients already diagnosed from a certain disease of interest who survived beyond the cross‐section date. Clearly, such a sampling design implies an observational bias, in the sense that individuals with longer survival (the 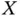 value) will be observed with a relatively large probability. There exist well investigated proposals to overcome such a bias, based on the simple idea of taking the observed left‐truncation times into account to define suitable risk sets. For this purpose, independence between
value) will be observed with a relatively large probability. There exist well investigated proposals to overcome such a bias, based on the simple idea of taking the observed left‐truncation times into account to define suitable risk sets. For this purpose, independence between 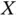 and
and 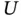 has been traditionally assumed. This independence assumption states that the time‐to‐event distribution remains unchanged along time, being unrelated to the date of onset. A classical example of left‐truncation are the Channing House data, where the age at death is measured for people living in that retirement centre; in this case, the target variable is left‐truncated by the age when entering the residence (Klein and Moeschberger, 2003).
has been traditionally assumed. This independence assumption states that the time‐to‐event distribution remains unchanged along time, being unrelated to the date of onset. A classical example of left‐truncation are the Channing House data, where the age at death is measured for people living in that retirement centre; in this case, the target variable is left‐truncated by the age when entering the residence (Klein and Moeschberger, 2003).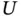 after onset. For example, diagnosis of a certain disease may not be ascertained until the first visit to the hospital. If the 'end‐of‐disease' event occurs before the potential date of visit, the time‐to‐event of such a patient will be never known, with the resulting difficulty in observing relatively small event times. Beyersmann et al. (2012) provide an illustrative example of this issue in the investigation of abortion times.
after onset. For example, diagnosis of a certain disease may not be ascertained until the first visit to the hospital. If the 'end‐of‐disease' event occurs before the potential date of visit, the time‐to‐event of such a patient will be never known, with the resulting difficulty in observing relatively small event times. Beyersmann et al. (2012) provide an illustrative example of this issue in the investigation of abortion times.










