In some particular settings, the target variable of ultimate interest 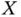 is observed only for the individuals who experience the event before a certain calendar time
is observed only for the individuals who experience the event before a certain calendar time 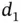 . A typical example of such a situation is the investigation of the incubation (or induction) times for AIDS; see for example Klein and Moeschberger (2003). The incubation time is defined as the time elapsed between the date of HIV infection,
. A typical example of such a situation is the investigation of the incubation (or induction) times for AIDS; see for example Klein and Moeschberger (2003). The incubation time is defined as the time elapsed between the date of HIV infection, 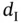 say, and the development of AIDS. If
say, and the development of AIDS. If 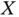 stands for the incubation time and
stands for the incubation time and 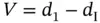 , then the incubation times of individuals developing AIDS prior
, then the incubation times of individuals developing AIDS prior 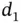 follow the distribution of
follow the distribution of 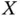 conditionally on
conditionally on 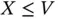 . Here,
. Here, 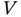 is called the right‐truncation time. An immediate effect of right‐truncation is that large values of
is called the right‐truncation time. An immediate effect of right‐truncation is that large values of 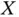 are sampled with a relatively small probability.
are sampled with a relatively small probability.
1.2.3 Truncation vs. Censoring
At this point, the reader may be curious about the difference between truncation and censoring. Right‐censoring is a very well known phenomenon in Survival Analysis and reliability studies, among other fields. It happens when the follow‐up of a given individual stops before the event of interest has taken place. In such a case, the observer only knows that the target variable is larger than the registered value, which is referred to as censoring time. A sample made up of real and censored values is typically analysed by the Kaplan–Meier estimator (Kaplan and Meier, 1958), which corrects for the fact that some of the recorded values for  are smaller than the true ones. With truncated data, every value in the sample corresponds to a true observation of
are smaller than the true ones. With truncated data, every value in the sample corresponds to a true observation of 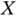 ; however, the distribution of the observed values may be shifted with respect to the true one due to the truncation event. This difference between truncation and censoring suggests that specific methods to estimate the target distribution under random truncation should be employed. Indeed, Woodroofe (1985) provides a deep analysis of one‐sided truncation, introducing the original idea of Lynden–Bell (1971) as a nonparametric maximum likelihood estimator (NPMLE) of the probability distribution in that setting. The estimator in Woodroofe (1985) is a particular case of the estimator corresponding to doubly truncated data, on which this book is focused.
; however, the distribution of the observed values may be shifted with respect to the true one due to the truncation event. This difference between truncation and censoring suggests that specific methods to estimate the target distribution under random truncation should be employed. Indeed, Woodroofe (1985) provides a deep analysis of one‐sided truncation, introducing the original idea of Lynden–Bell (1971) as a nonparametric maximum likelihood estimator (NPMLE) of the probability distribution in that setting. The estimator in Woodroofe (1985) is a particular case of the estimator corresponding to doubly truncated data, on which this book is focused.
A variable of interest 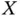 is said to be doubly truncated by a couple of random variables
is said to be doubly truncated by a couple of random variables 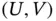 if the observation of
if the observation of 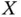 is possible only when
is possible only when 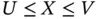 occurs. In such a case,
occurs. In such a case, 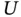 and
and 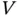 are called left‐ and right‐truncation variables respectively. Double truncation reduces to left‐truncation when
are called left‐ and right‐truncation variables respectively. Double truncation reduces to left‐truncation when 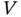 degenerates at
degenerates at 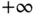 , while it corresponds to right‐truncation when
, while it corresponds to right‐truncation when 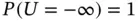 . This book is focused on the problem of estimating the distribution of
. This book is focused on the problem of estimating the distribution of 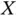 , and other related curves, from a set of iid triplets with the distribution of
, and other related curves, from a set of iid triplets with the distribution of 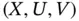 given
given 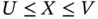 .
.
There are several scenarios where double truncation appears in practice. One setting leading to double truncation is that of interval sampling, where the sample is restricted to the individuals with event between two specific dates  and
and 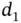 (Zhu and Wang, 2012). Then, the right‐truncation time is
(Zhu and Wang, 2012). Then, the right‐truncation time is 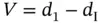 , where
, where 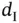 denotes the date of onset for the time‐to‐event, and the left‐truncation time is
denotes the date of onset for the time‐to‐event, and the left‐truncation time is 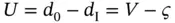 , where
, where 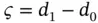 is the interval width. The Childhood Cancer Data in Section 1.4.1is an example of data obtained through interval sampling.
is the interval width. The Childhood Cancer Data in Section 1.4.1is an example of data obtained through interval sampling.
Читать дальше

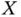 is observed only for the individuals who experience the event before a certain calendar time
is observed only for the individuals who experience the event before a certain calendar time 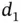 . A typical example of such a situation is the investigation of the incubation (or induction) times for AIDS; see for example Klein and Moeschberger (2003). The incubation time is defined as the time elapsed between the date of HIV infection,
. A typical example of such a situation is the investigation of the incubation (or induction) times for AIDS; see for example Klein and Moeschberger (2003). The incubation time is defined as the time elapsed between the date of HIV infection, 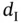 say, and the development of AIDS. If
say, and the development of AIDS. If 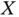 stands for the incubation time and
stands for the incubation time and 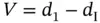 , then the incubation times of individuals developing AIDS prior
, then the incubation times of individuals developing AIDS prior 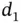 follow the distribution of
follow the distribution of 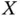 conditionally on
conditionally on 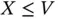 . Here,
. Here, 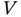 is called the right‐truncation time. An immediate effect of right‐truncation is that large values of
is called the right‐truncation time. An immediate effect of right‐truncation is that large values of 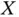 are sampled with a relatively small probability.
are sampled with a relatively small probability. are smaller than the true ones. With truncated data, every value in the sample corresponds to a true observation of
are smaller than the true ones. With truncated data, every value in the sample corresponds to a true observation of 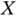 ; however, the distribution of the observed values may be shifted with respect to the true one due to the truncation event. This difference between truncation and censoring suggests that specific methods to estimate the target distribution under random truncation should be employed. Indeed, Woodroofe (1985) provides a deep analysis of one‐sided truncation, introducing the original idea of Lynden–Bell (1971) as a nonparametric maximum likelihood estimator (NPMLE) of the probability distribution in that setting. The estimator in Woodroofe (1985) is a particular case of the estimator corresponding to doubly truncated data, on which this book is focused.
; however, the distribution of the observed values may be shifted with respect to the true one due to the truncation event. This difference between truncation and censoring suggests that specific methods to estimate the target distribution under random truncation should be employed. Indeed, Woodroofe (1985) provides a deep analysis of one‐sided truncation, introducing the original idea of Lynden–Bell (1971) as a nonparametric maximum likelihood estimator (NPMLE) of the probability distribution in that setting. The estimator in Woodroofe (1985) is a particular case of the estimator corresponding to doubly truncated data, on which this book is focused.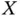 is said to be doubly truncated by a couple of random variables
is said to be doubly truncated by a couple of random variables 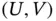 if the observation of
if the observation of 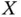 is possible only when
is possible only when 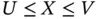 occurs. In such a case,
occurs. In such a case, 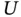 and
and 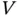 are called left‐ and right‐truncation variables respectively. Double truncation reduces to left‐truncation when
are called left‐ and right‐truncation variables respectively. Double truncation reduces to left‐truncation when 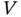 degenerates at
degenerates at 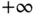 , while it corresponds to right‐truncation when
, while it corresponds to right‐truncation when 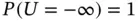 . This book is focused on the problem of estimating the distribution of
. This book is focused on the problem of estimating the distribution of 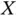 , and other related curves, from a set of iid triplets with the distribution of
, and other related curves, from a set of iid triplets with the distribution of 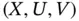 given
given 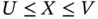 .
. and
and 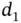 (Zhu and Wang, 2012). Then, the right‐truncation time is
(Zhu and Wang, 2012). Then, the right‐truncation time is 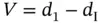 , where
, where 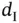 denotes the date of onset for the time‐to‐event, and the left‐truncation time is
denotes the date of onset for the time‐to‐event, and the left‐truncation time is 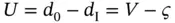 , where
, where 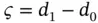 is the interval width. The Childhood Cancer Data in Section 1.4.1is an example of data obtained through interval sampling.
is the interval width. The Childhood Cancer Data in Section 1.4.1is an example of data obtained through interval sampling.










