1 ...6 7 8 10 11 12 ...41 A. 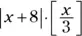 . The dot between the absolute value and greatest integer operations isn’t really necessary, but it helps define better what you’re expressing.
. The dot between the absolute value and greatest integer operations isn’t really necessary, but it helps define better what you’re expressing.
13  Use mathematical symbols to write the expression: “Four times z plus the square root of 11.”
Use mathematical symbols to write the expression: “Four times z plus the square root of 11.”
14 Use mathematical symbols to write the expression: “The difference between x and two is divided by pi.”
15 Use mathematical symbols to write the expression: “The product of six and the absolute value of the sum of eight and y is divided by the square root of the difference between 9 and x .”
Taking Aim at Algebra-Speak
Everything you study requires some understanding of the vocabulary and any special notation. When you can use one word like “introductory” instead of “all that good stuff that comes before the meat of the matter,” then you’ve saved time and space and gotten to the point quickly.
Algebra is full of good words and symbols, as you see in the previous section. And now you find how specific symbols and wording gets right to the point (and, yes, a point in algebra can mean multiply). You’re “equal” to the challenge!
Herding numbers with grouping symbols
Before a car manufacturer puts together a car, several different things have to be done first. The engine experts have to construct the engine with all its parts. The body of the car then has to be mounted onto the chassis and also secured. Other car assemblers have to perform the tasks that they specialize in as well. When these tasks are all accomplished in order, the car can be put together. The same is true with algebra. You have to do what’s inside the grouping symbol before you can use the result in the rest of the equation.
Grouping symbols tell you that you have to deal with the terms inside the grouping symbols before you deal with the larger problem. If the problem contains grouped items, do what’s inside a grouping symbol first, and then follow the order of operations. The grouping symbols are as follows.
Parentheses ( ): Parentheses are the most commonly used symbols for grouping.
Brackets [ ] and braces { }: Brackets and braces are also used frequently for grouping and have the same effect as parentheses. Using the different types of symbols helps when there’s more than one grouping in a problem. It’s easier to tell where a group starts and ends.
Radical : This is used for finding roots.
Fraction line (called the vinculum ): The fraction line also acts as a grouping symbol — everything above the line (in the numerator ) is grouped together, and everything below the line (in the denominator ) is grouped together.
Even though the order of operations and grouping-symbol rules are fairly straightforward, it’s hard to describe, in words, all the situations that can come up in these problems. The explanations and examples in Chapters 3and 7should clear up any questions you may have.
 Q.What are the operations found in the expression:
Q.What are the operations found in the expression: 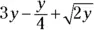 ?
?
A.The operations, in order from left to right, are multiplication, subtraction, division, addition, multiplication, and square root. The term 3 y means to multiply 3 times y . The subtraction symbol separates the first and second terms. Writing y over 4 in a fraction means to divide. Then that term has the radical added to it. The 2 and y are multiplied under the radical, and then the square root is taken.
Q.Identify the grouping symbols shown in 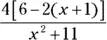 .
.
A.The first grouping symbol to recognize is the fraction line. It separates the term in the numerator, 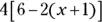 , from the terms in the denominator,
, from the terms in the denominator, 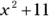 . Next, you see the brackets, which contain the two terms forming a subtraction,
. Next, you see the brackets, which contain the two terms forming a subtraction, 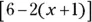 . The last grouping symbols are the parentheses, which have a multiplier of 2 and, inside, the sum of two terms.
. The last grouping symbols are the parentheses, which have a multiplier of 2 and, inside, the sum of two terms.
16  Write the expression using the correct symbols: “The square root of x is subtracted from 3 times y .”
Write the expression using the correct symbols: “The square root of x is subtracted from 3 times y .”
17 Write the expression using the correct symbols: “Add 2 and y ; then divide that sum by 11.”
18 Identify the grouping symbols in 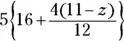 .
.
Algebra is all about relationships — not the he-loves-me-he-loves-me-not kind of relationship, but the relationships between numbers or among the terms of an expression. Although algebraic relationships can be just as complicated as romantic ones, you have a better chance of understanding an algebraic relationship. The symbols for the relationships are given here. The equations are found in Chapters 14through 18, and inequalities are found in Chapter 19.
= means that the first value is equal to or the same as the value that follows.
≠ means that the first value is not equal to the value that follows.
≈ means that one value is approximately the same or about the same as the value that follows; this is used when rounding numbers.
≤ means that the first value is less than or equal to the value that follows.
< means that the first value is less than the value that follows.
≥ means that the first value is greater than or equal to the value that follows.
> means that the first value is greater than the value that follows.
 Q.Write this expression using mathematical symbols: “When you square the sum of x and 4, the result is greater than or equal to 23.”
Q.Write this expression using mathematical symbols: “When you square the sum of x and 4, the result is greater than or equal to 23.”
A.  . The point of the inequality symbol always faces the smaller value.
. The point of the inequality symbol always faces the smaller value.
Q.Write this expression using mathematical symbols: “The circumference, C, of a circle divided by the diameter, d, is equal to pi, which is about 3.1416.”
Читать дальше

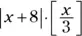 . The dot between the absolute value and greatest integer operations isn’t really necessary, but it helps define better what you’re expressing.
. The dot between the absolute value and greatest integer operations isn’t really necessary, but it helps define better what you’re expressing. Use mathematical symbols to write the expression: “Four times z plus the square root of 11.”
Use mathematical symbols to write the expression: “Four times z plus the square root of 11.” Q.What are the operations found in the expression:
Q.What are the operations found in the expression: 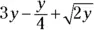 ?
?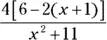 .
.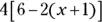 , from the terms in the denominator,
, from the terms in the denominator, 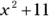 . Next, you see the brackets, which contain the two terms forming a subtraction,
. Next, you see the brackets, which contain the two terms forming a subtraction, 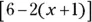 . The last grouping symbols are the parentheses, which have a multiplier of 2 and, inside, the sum of two terms.
. The last grouping symbols are the parentheses, which have a multiplier of 2 and, inside, the sum of two terms.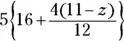 .
. . The point of the inequality symbol always faces the smaller value.
. The point of the inequality symbol always faces the smaller value.










