A coefficient is another type of constant. It is a multiplier of a variable. In the equation , a and b are coefficients. They have constant, assigned values and are factors, but they have the special role of multiplying variables.
An exponent is a small number written slightly above and to the right of a variable or number, such as the 2 in the expression 32. It’s used to show repeated multiplication. An exponent is also called the power of the value. For more on exponents, see Chapter 5.
 Q.Identify the terms, coefficients, factors, exponents, and constants in the expression
Q.Identify the terms, coefficients, factors, exponents, and constants in the expression 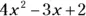 .
.
A.There are three terms, separated by the subtraction and addition symbols. In the first term, the 4 is the coefficient, and the 4 and  are factors. The 2 is the exponent. In the second term, the 3 and the x are factors. The exponent 1 isn’t shown on the x ; it’s just assumed. And the final term, the 2, is a constant.
are factors. The 2 is the exponent. In the second term, the 3 and the x are factors. The exponent 1 isn’t shown on the x ; it’s just assumed. And the final term, the 2, is a constant.
Q.Identify the terms, coefficients, factors, exponents, and constants in the expression 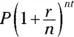 .
.
A.This expression has just one term. The P is a factor, and the parentheses form the other factor. There are two terms in the parentheses, and the exponent on the parentheses is nt .
9  How many terms are there in the expression:
How many terms are there in the expression: 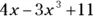 ?
?
10 How many factors are found in the expression: 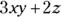 ?
?
11 Which are the variables and which are the constants in the expression: 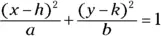 ?
?
12 Which are the exponents in the expression: 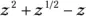 ?
?
Describing the size of an expression
An expression is a combination of terms and operations and can take on many different formats. In Chapters 11through 16, you see many types of expressions and several types of equations that are created from the expressions. Many of these expressions and equations have very precise and descriptive names.
A polynomial is an expression containing variables and constants. It consists of one or more terms. The terms are separated by addition and subtraction. And the exponents on the variable terms are always whole numbers, never fractions or negative numbers.Ex:
A monomial is a polynomial consisting of exactly 1 term.Ex:
A binomial is a polynomial consisting of exactly 2 terms.Ex:
A trinomial is a polynomial consisting of exactly 3 terms.Ex:
A linear expression is a polynomial in which there is no variable with an exponent greater than 1. In fact, the exponents can be only 1 or 0. And there must be at least one variable term with an exponent of 1.Ex:
A quadratic expression is a polynomial in which there is no variable with an exponent greater than 2. In fact, the exponents can be only 2, 1, or 0. And there must be at least one variable term with an exponent of 2.Ex.
Relating operations with symbols
The basics of algebra involve symbols. Algebra uses symbols for quantities, operations, relations, or grouping. The symbols are shorthand and are much more efficient than writing out the words or meanings. But you need to know what the symbols represent, and the following list shares some of that information. The operations are covered thoroughly in Chapter 6.
+ means add or find the sum or more than or increased by; the result of addition is the sum. It also is used to indicate a positive number.
– means subtract or minus or decreased by or less; the result is the difference. It’s also used to indicate a negative number.
× means multiply or times. The values being multiplied together are the multipliers or factors; the result is the product. Some other symbols meaning multiply can be grouping symbols: ( ), [ ], { }, ·, *. In algebra, the × symbol is used infrequently because it can be confused with the variable x. The symbol is popular because it’s easy to write. The grouping symbols are used when you need to contain many terms or a messy expression. By themselves, the grouping symbols don’t mean to multiply, but if you put a value in front of or behind a grouping symbol, it means to multiply.
÷ means divide . The number that’s going into the dividend is the divisor. The result is the quotient. Other signs that indicate division are the fraction line and slash, /.
means to take the square root of something — to find the number, which, multiplied by itself, gives you the number under the sign. (See Chapter 6for more on square roots.)
means to find the absolute value of a number, which is the number itself or its distance from 0 on the number line. (For more on absolute value, turn to Chapter 2.)
π is the Greek letter pi that refers to the irrational number: 3.14159. It represents the relationship between the diameter and circumference of a circle.
is the greatest integer operation. It tells you to evaluate what’s in the brackets and replace it with the biggest integer that is not larger than what’s in them.
 Q.Use mathematical symbols to write the expression: “The product of 6 and a is divided by the difference between the square of a and 1 and added to the square root of the difference between pi and r cubed.”
Q.Use mathematical symbols to write the expression: “The product of 6 and a is divided by the difference between the square of a and 1 and added to the square root of the difference between pi and r cubed.”
A. 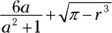 . You don’t need a dot between the 6 and the a . Writing the two factors together indicates a product. Putting the binomial
. You don’t need a dot between the 6 and the a . Writing the two factors together indicates a product. Putting the binomial  in the denominator indicates that you’re dividing the 6 a by that expression. The exponent of 3 indicates r is being cubed. The two terms in the difference both appear under the radical.
in the denominator indicates that you’re dividing the 6 a by that expression. The exponent of 3 indicates r is being cubed. The two terms in the difference both appear under the radical.
Q.Use mathematical symbols to write the expression: “The absolute value of the sum of x and 8 times the greatest integer value of the quotient of x and 3.”
Читать дальше

 Q.Identify the terms, coefficients, factors, exponents, and constants in the expression
Q.Identify the terms, coefficients, factors, exponents, and constants in the expression 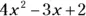 .
. are factors. The 2 is the exponent. In the second term, the 3 and the x are factors. The exponent 1 isn’t shown on the x ; it’s just assumed. And the final term, the 2, is a constant.
are factors. The 2 is the exponent. In the second term, the 3 and the x are factors. The exponent 1 isn’t shown on the x ; it’s just assumed. And the final term, the 2, is a constant.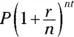 .
. How many terms are there in the expression:
How many terms are there in the expression: 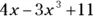 ?
?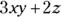 ?
? ?
?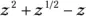 ?
?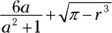 . You don’t need a dot between the 6 and the a . Writing the two factors together indicates a product. Putting the binomial
. You don’t need a dot between the 6 and the a . Writing the two factors together indicates a product. Putting the binomial  in the denominator indicates that you’re dividing the 6 a by that expression. The exponent of 3 indicates r is being cubed. The two terms in the difference both appear under the radical.
in the denominator indicates that you’re dividing the 6 a by that expression. The exponent of 3 indicates r is being cubed. The two terms in the difference both appear under the radical.










