Integers are popular in algebra. When you solve a long, complicated problem and come up with an integer, you can be joyous because your answer is probably right. After all, it’s not a fraction! This doesn’t mean that answers in algebra can’t be fractions or decimals. It’s just that most textbooks and reference books try to stick with nice answers to increase the comfort level and avoid confusion. This is my plan in this book, too. After all, who wants a messy answer — even though, in real life, that’s more often the case. I use integers in Chapter 14and those later on, where you find out how to solve equations.
Being reasonable: Rational numbers
Rational numbers act rationally! What does that mean? In this case, acting rationally means that the decimal equivalent of the rational number behaves. The decimal eventually ends somewhere, or it has a repeating pattern to it. That’s what constitutes “behaving.”
Some rational numbers have decimals that end such as: 3.4, 5.77623, –4.5. Other rational numbers have decimals that repeat the same pattern, such as  , or
, or 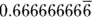 . The horizontal bar over the 164 and the 6 lets you know that these numbers repeat forever.
. The horizontal bar over the 164 and the 6 lets you know that these numbers repeat forever.
In all cases, rational numbers can be written as fractions. Each rational number has a fraction that it’s equal to. So one definition of a rational number is any number that can be written as a fraction, 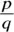 , where p and q are integers (except q can’t be 0). If a number can’t be written as a fraction, then it isn’t a rational number. Rational numbers appear in Chapter 16, where you see quadratic equations, and later, when the applications are presented.
, where p and q are integers (except q can’t be 0). If a number can’t be written as a fraction, then it isn’t a rational number. Rational numbers appear in Chapter 16, where you see quadratic equations, and later, when the applications are presented.
Restraining irrational numbers
Irrational numbers are just what you may expect from their name: the opposite of rational numbers. An irrational number cannot be written as a fraction, and decimal values for irrationals never end and never have a nice pattern to them. Whew! Talk about irrational! For example, π, with its never-ending decimal places, is irrational. Irrational numbers are often created when using the quadratic formula, as you see in Chapter 16, because you find the square roots of numbers that are not perfect squares, such as: 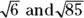 .
.
Picking out primes and composites
A number is considered to be prime if it can be divided evenly only by 1 and by itself. The prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and so on. The only prime number that’s even is 2, the first prime number. Mathematicians have been studying prime numbers for centuries, and prime numbers have them stumped. No one has ever found a formula for producing all the primes. Mathematicians just assume that prime numbers go on forever.
A number is composite if it isn’t prime — if it can be divided by at least one number other than 1 and itself. So the number 12 is composite because it’s divisible by 1, 2, 3, 4, 6, and 12. Chapter 8deals with primes, but you also see them throughout the chapters, where I show you how to factor primes out of expressions.
Numbers can be classified in more than one way, the same way that a person can be classified as male or female, tall or short, blonde or brunette, and so on. The number –3 is negative, it’s an integer, it’s an odd number, it’s rational, and it’s real. The number –3 is also a negative prime number. You should be familiar with all these classifications so that you can read mathematics correctly.
Zero is a very special number. It wasn’t really used in any of the earliest counting systems. In fact, there is no symbol for zero in the Roman numerals!
Zero is a very useful number, but it also comes with its challenges. You can’t divide by zero, but you can add zero to a number and multiply a number by 0. You’ll find zero popping up in the most interesting places!
Imagining imaginary numbers
Yes, there are imaginary numbers in mathematics. These numbers were actually created by mathematicians who didn’t like not finishing a problem! They would be trying to solve a quadratic equation and be stumped by the situation where they needed the square root of a negative number. There was no way to deal with this.
So some clever mathematicians came up with a solution. They declared that 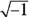 must be equal to i . Yes, the i stands for “imaginary.” You’ll see how this works in Chapter 16.
must be equal to i . Yes, the i stands for “imaginary.” You’ll see how this works in Chapter 16.
Coping with complex numbers
A complex number isn’t really all that mysterious. This is just a designation that allows for you to deal with both real and imaginary parts of a number. A complex number has some of each! Complex numbers have the general format of 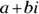 , where a and b are real numbers, and the i is that imaginary number,
, where a and b are real numbers, and the i is that imaginary number, 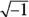 .
.
 Q.Using the choices: natural, whole, integer, rational, irrational, prime, and imaginary, which of these can be used to describe the number 8?
Q.Using the choices: natural, whole, integer, rational, irrational, prime, and imaginary, which of these can be used to describe the number 8?
A. Natural, whole, integer, rational.The number 8 fits all of these descriptions. It is rational, because you can write it as a fraction such as 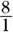 or
or 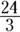 .
.
Q.Using the choices: natural, whole, integer, rational, irrational, prime, and imaginary, which of these can be used to describe the number 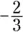 ?
?
A. Rational.This is written as a fraction but cannot be reduced to create an integer.
Q.Using the choices: natural, whole, integer, rational, irrational, prime, and imaginary, which of these can be used to describe the number 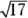 ?
?
A. Irrational.The number 17 isn’t a perfect square, so the decimal equivalence of 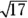 is a decimal that goes on forever without repeating or terminating.
is a decimal that goes on forever without repeating or terminating.
Q.Using the choices: natural, whole, integer, rational, irrational, prime, and imaginary, which of these can be used to describe the number  ?
?
Читать дальше

 , or
, or 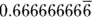 . The horizontal bar over the 164 and the 6 lets you know that these numbers repeat forever.
. The horizontal bar over the 164 and the 6 lets you know that these numbers repeat forever.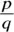 , where p and q are integers (except q can’t be 0). If a number can’t be written as a fraction, then it isn’t a rational number. Rational numbers appear in Chapter 16, where you see quadratic equations, and later, when the applications are presented.
, where p and q are integers (except q can’t be 0). If a number can’t be written as a fraction, then it isn’t a rational number. Rational numbers appear in Chapter 16, where you see quadratic equations, and later, when the applications are presented.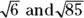 .
.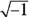 must be equal to i . Yes, the i stands for “imaginary.” You’ll see how this works in Chapter 16.
must be equal to i . Yes, the i stands for “imaginary.” You’ll see how this works in Chapter 16.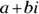 , where a and b are real numbers, and the i is that imaginary number,
, where a and b are real numbers, and the i is that imaginary number, 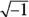 .
. Q.Using the choices: natural, whole, integer, rational, irrational, prime, and imaginary, which of these can be used to describe the number 8?
Q.Using the choices: natural, whole, integer, rational, irrational, prime, and imaginary, which of these can be used to describe the number 8?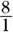 or
or 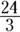 .
.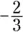 ?
?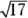 ?
?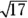 is a decimal that goes on forever without repeating or terminating.
is a decimal that goes on forever without repeating or terminating. ?
?










