9 Book 5: Solving Linear and Polynomial Equations Chapter 14: Establishing Ground Rules for Solving Equations Creating the Correct Setup for Solving Equations Keeping Equations Balanced Solving with Reciprocals Making a List and Checking It Twice Practice Problems Answers and Explanations Whaddya Know? Chapter 14 Quiz Answers to Chapter 14 Quiz Chapter 15: Lining Up Linear Equations Playing by the Rules Using the Addition/Subtraction Property Using the Multiplication/Division Property Putting Several Operations Together Solving Linear Equations with Grouping Symbols Working with Proportions Solving for Variables in Formulas Practice Questions Answers and Explanations Whaddya Know? Chapter 15 Quiz Answers to Chapter 15 Quiz Chapter 16: Muscling Up to Quadratic Equations Using the Square-Root Rule Factoring for a Solution Solving Quadratics with Three Terms Using the Quadratic Formula Completing the Square Imagining the Worst with Imaginary Numbers Practice Problems Answers and Explanations Whaddya Know? Chapter 16 Quiz Answers to Chapter 16 Quiz
10 Book 6: Dealing with Non-Polynomial Equations and Inequalities Chapter 17: Yielding to Higher Powers Queuing Up to Cubic Equations Determining How Many Possible Roots Applying the Rational Root Theorem Using the Factor/Root Theorem Solving by Factoring Solving Powers That Are Quadratic-Like Solving Synthetically Practice Questions Answers and Explanations Whaddya Know? Chapter 17 Quiz Answers to Chapter 17 Quiz Chapter 18: Reeling in Radical and Absolute Value Equations Raising Both Sides to Solve Radical Equations Doubling the Fun with Radical Equations Solving Absolute Value Equations Checking for Absolute Value Extraneous Roots Practice Questions Answers and Explanations Whaddya Know? Chapter 18 Quiz Answers to Chapter 18 Quiz Chapter 19: Getting Even with Inequalities Defining the Inequality Notation Using the Rules to Work on Inequality Statements Rewriting Inequalities Using Interval Notation Solving Linear Inequalities Solving Quadratic Inequalities Dealing with Polynomial and Rational Inequalities Solving Absolute-Value Inequalities Solving Complex Inequalities Practice Questions Answers and Explanations Whaddya Know? Chapter 19 Quiz Answers to Chapter 19 Quiz
11 Book 7: Evaluating Formulas and Story Problems Chapter 20: Facing Up to Formulas Working with Formulas Measuring Up Deciphering Perimeter, Area, and Volume Getting Interested in Using Percent Working out the Combinations and Permutations Practice Questions Answers and Explanations Whaddya Know? Chapter 20 Quiz Answers to Chapter 20 Quiz Chapter 21: Making Formulas Work in Basic Story Problems Setting Up to Solve Story Problems Applying the Pythagorean Theorem Using Geometry to Solve Story Problems Working around Perimeter, Area, and Volume Going ’Round in Circles Putting Distance, Rate, and Time in a Formula Counting on Interest and Percent Practice Questions Answers and Explanations Whaddya Know? Chapter 21 Quiz Answers to Chapter 21 Quiz Chapter 22: Relating Values in Story Problems Tackling Age Problems Tackling Consecutive Integer Problems Working Together on Work Problems Throwing an Object into the Air Practice Questions Answers and Explanations Whaddya Know? Chapter 22 Quiz Answers to Chapter 22 Quiz Chapter 23: Measuring Up with Quality and Quantity Story Problems Achieving the Right Blend with Mixture Problems Concocting the Correct Solution 100% of the Time Dealing with Money Problems Practice Questions Answers and Explanations Whaddya Know? Chapter 23 Quiz Answers to Chapter 23 Quiz
12 Book 8: Getting a Grip on Graphing Chapter 24: Getting a Handle on Graphing Thickening the Plot with Points Graphing Lines Computing Slopes of Lines Writing Equations of Lines Picking on Parallel and Perpendicular Lines Finding Distances between Points Finding Midpoints of Segments Practice Questions Answers and Explanations Whaddya Know? Chapter 24 Quiz Answers to Chapter 24 Quiz Chapter 25: Extending the Graphing Horizon Finding the Intersections of Lines Graphing Parabolas and Circles Curling Up with Parabolas Plotting and Plugging in Polynomial Graphs Investigating Graphs of Inequality Functions Taking on Absolute-Value Function Graphs Graphing with Transformations Practice Questions Answers and Explanations Whaddya Know? Chapter 25 Quiz Answers to Chapter 25 Quiz Chapter 26: Coordinating Systems of Equations and Graphing Defining Solutions of Systems of Equations Solving Systems of Linear Equations Solving Systems Involving Non-Linear Equations Taking on Systems of Three Linear Equations Practice Problems Answers and Explanations Whaddya Know? Chapter 26 Quiz Answers to Chapter 26 Quiz
13 Index
14 About the Author
15 Connect with Dummies
16 End User License Agreement
1 Chapter 2 TABLE 2-1 Comparing Positive and Negative Numbers
2 Chapter 8TABLE 8-1 Rules of Divisibility
3 Chapter 24TABLE 24-1 QuadrantsTABLE 24-2 Axes
1 Chapter 1FIGURE 1-1: A number line from 0 to 5 with half-unit increments.FIGURE 1-2: A number line from –10 to 10 with one-unit increments.
2 Chapter 2FIGURE 2-1: A number line.FIGURE 2-2: Another number line.FIGURE 2-3: Positive and negative numbers on a number line.
3 Chapter 8FIGURE 8-1: Finding the prime factors using a tree.
4 Chapter 9FIGURE 9-1: Pascal’s Triangle can help you find powers of binomials.
5 Chapter 19FIGURE 19-1: The graphs of greater-than and less-than-or-equal-to.FIGURE 19-2: A graph of the inequality.FIGURE 19-3: A graph of the interval.FIGURE 19-4: A graph of the inequality.FIGURE 19-5: A graph of the interval.FIGURE 19-6: A graph of an inequality.FIGURE 19-7: A graph of an inequality.FIGURE 19-8: A number line helps you find the signs of the factors and their pr...FIGURE 19-9: Filling in the signs between the critical numbers.FIGURE 19-10: The sign changes at each critical number in this problem.FIGURE 19-11: The sign of the quotient is shown.FIGURE 19-12: The 1 and –1 are included in the solution.
6 Chapter 20FIGURE 20-1: Triangulating the “right” way.
7 Chapter 21FIGURE 21-1: Fencing three sides of the field.FIGURE 21-2: Volume is determined by multiplying length, width, and height.FIGURE 21-3: Some people believe pyramids have preservation powers.FIGURE 21-4: Basketballs, globes, planets, and sometimes oranges are spheres.FIGURE 21-5: The diameter is the longest distance across a circle.FIGURE 21-6: The corral along a river.FIGURE 21-7: ABC is similar to DEF.FIGURE 21-8: Trapezoidal room.
8 Chapter 23FIGURE 23-1: Visualizing containers can help with mixture problems.FIGURE 23-2: Assigning prices and pounds.
9 Chapter 24FIGURE 24-1: Identifying quadrants.FIGURE 24-2: Graphing 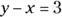 .FIGURE 24-3: Horizontal lines are parallel to the x-axis.FIGURE 24-4: When all the x-coordinates are the same, you get a vertical line.FIGURE 24-5: Pick a line — see its slope.FIGURE 24-6: Horizontal lines have a 0 slope. Vertical lines have an undefined ...FIGURE 24-7: Parallel lines are like railroad tracks; perpendicular lines meet ...
.FIGURE 24-3: Horizontal lines are parallel to the x-axis.FIGURE 24-4: When all the x-coordinates are the same, you get a vertical line.FIGURE 24-5: Pick a line — see its slope.FIGURE 24-6: Horizontal lines have a 0 slope. Vertical lines have an undefined ...FIGURE 24-7: Parallel lines are like railroad tracks; perpendicular lines meet ...
10 Chapter 25FIGURE 25-1: The intersection of two lines at a point (1,–2).FIGURE 25-2: The simplest parabola.FIGURE 25-3: A steeper parabola and a flatter parabola.FIGURE 25-4: Parabolas spooning.FIGURE 25-5: Pretty parabolas all in a row.FIGURE 25-6: The circle has a radius of 5.FIGURE 25-7: The x-intercepts and the graph of the polynomial.FIGURE 25-8: The intercepts help with the graph of the polynomial.FIGURE 25-9: Use a dashed line when the line is not included.FIGURE 25-10: The origin is included in the solution.FIGURE 25-11: The negative values are flipped over the x-axis.FIGURE 25-12: The 2 multiplier steepens the graph.FIGURE 25-13: Parabolas galore.
Читать дальше

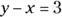 .FIGURE 24-3: Horizontal lines are parallel to the x-axis.FIGURE 24-4: When all the x-coordinates are the same, you get a vertical line.FIGURE 24-5: Pick a line — see its slope.FIGURE 24-6: Horizontal lines have a 0 slope. Vertical lines have an undefined ...FIGURE 24-7: Parallel lines are like railroad tracks; perpendicular lines meet ...
.FIGURE 24-3: Horizontal lines are parallel to the x-axis.FIGURE 24-4: When all the x-coordinates are the same, you get a vertical line.FIGURE 24-5: Pick a line — see its slope.FIGURE 24-6: Horizontal lines have a 0 slope. Vertical lines have an undefined ...FIGURE 24-7: Parallel lines are like railroad tracks; perpendicular lines meet ...










