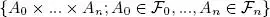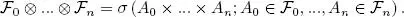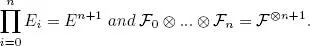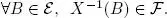Among the elementary properties of σ -algebra, we can cite stability through any intersection (countable or not).
PROPOSITION 1.1.– Any intersection of σ-algebras over a set Ω is a σ-algebra over Ω.
PROOF.– Let (  i) i∈Ibe any family of σ -algebra indexed by a non-empty set I . Thus,
i) i∈Ibe any family of σ -algebra indexed by a non-empty set I . Thus,
– first of all, for any i, Ω ∈ i, thus Ω ∈ ∩i∈Ii;
– secondly, if A ∈ ∩i∈I i, then for any i, A ∈ i. As these are σ-algebras, we have that for any i, Ac ∈ i, thus Ac ∈ ∩i∈I i;
– finally, if for any n ∈ ℕ, An ∈ ∩i∈I i, then for any i, n, An ∈ i. As these are σ-algebras, we have that for any i, ∪n∈ℕAn ∈ i, thus
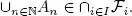

It is generally difficult to make explicit all the events in a σ -algebra. We often describe it using generating events.
DEFINITION 1.3.– Let ε be a subset of 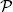 (Ω) . The σ-algebra σ (ε) generated by ε is the intersection of all σ-algebras containing ε . It is the smallest σ-algebra containing ε . ε is called the generating system of the σ-algebra σ ( ε ).
(Ω) . The σ-algebra σ (ε) generated by ε is the intersection of all σ-algebras containing ε . It is the smallest σ-algebra containing ε . ε is called the generating system of the σ-algebra σ ( ε ).
It can be seen that σ (ε) is indeed a σ -algebra, being an intersection of σ -algebras.
EXAMPLE 1.3.– If A ⊂ Ω , then, σ ( A ) = {∅, Ω , A, A c} is the smallest σ-algebra Ω containing A .

EXAMPLE 1.4.– If Ω is a topological space, the σ-algebra generated by the open sets of Ω is called the Borel σ-algebra of Ω . A Borel set is a set belonging to the Borel σ-algebra. On ℝ, 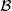 (ℝ) generally denotes the σ-algebra of Borel sets. It must be recalled that this is also the σ-algebra generated by the intervals, or by the intervals of the form ] − ∞ , x ] , x ∈ ℝ . Thus, there is no unicity of the generating system .
(ℝ) generally denotes the σ-algebra of Borel sets. It must be recalled that this is also the σ-algebra generated by the intervals, or by the intervals of the form ] − ∞ , x ] , x ∈ ℝ . Thus, there is no unicity of the generating system .

We will now recall the concept of the product σ -algebra.
DEFINITION 1.4.– Let ( E i,  i) i∈ℕ be a sequence of measurable spaces .
i) i∈ℕ be a sequence of measurable spaces .
– Let n ∈ ℕ. The σ-algebra defined over and generated by
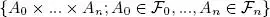
is denoted by  0⊗ ... ⊗
0⊗ ... ⊗  n , and it is called the product σ-algebra over We have, in particular ,
n , and it is called the product σ-algebra over We have, in particular ,
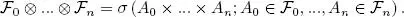
In the specific case where E 0= ... = E n= E and  0= ... =
0= ... =  n= , we also write
n= , we also write
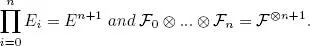
– We use ⊗i∈ℕi to denote the σ-algebra over the countable product space generated by the sets of the form where Ai ∈ i and Ai = Ei except for a finite number of indices i. In the specific case where, for any and i = , the product space is denoted by Eℕ, and the σ-algebra ⊗i∈ℕi is denoted by ⊗N.
Finally, let us review the concepts of measurability and measure.
DEFINITION 1.5.– Let Ω be non-empty set and  be a σ-algebra on Ω.
be a σ-algebra on Ω.
– A measure over a probabilizable space (Ω, ) is defined as any mapping μ defined over , with values in [0, +∞] = ℝ+ ∪ {+∞}, such that μ(∅) = 0 and for any family (Ai)i∈ℕ of pairwise disjoint elements of , we have the property of σ-additivity:
– A measure μ over a probabilizable space (Ω, ) is said to be finite, or have finite total mass, if μ(Ω) < ∞.
– If μ is a measure over a probabilizable space (Ω, ), then the triplet (Ω, , μ) is called a measured space.
DEFINITION 1.6.– Let (Ω,  ) and ( E , ε ) be two probabilizable spaces. A mapping X, defined over Ω taking values in E, is said to be (
) and ( E , ε ) be two probabilizable spaces. A mapping X, defined over Ω taking values in E, is said to be (  , ε ) -measurable, or just measurable, if there is no ambiguity regarding the reference σ-algebras, if
, ε ) -measurable, or just measurable, if there is no ambiguity regarding the reference σ-algebras, if
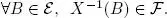
In practice, when E ⊂ ℝ, we set ε = 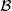 ( E ) the set of Borel subsets of E , that is, the set of subsets of E . We can simply say that X is
( E ) the set of Borel subsets of E , that is, the set of subsets of E . We can simply say that X is  -measurable. When, in addition, we manipulate a single σ -algebra
-measurable. When, in addition, we manipulate a single σ -algebra  over Ω, it can be simply said that X is measurable. If we work with several σ -algebras over Ω, the concerned σ -algebra must always be specified: X is
over Ω, it can be simply said that X is measurable. If we work with several σ -algebras over Ω, the concerned σ -algebra must always be specified: X is  -measurable.
-measurable.
EXAMPLE 1.5.– If (Ω,  ) is a measurable space and A ∈ , then the indicator function
) is a measurable space and A ∈ , then the indicator function
Читать дальше

 i) i∈Ibe any family of σ -algebra indexed by a non-empty set I . Thus,
i) i∈Ibe any family of σ -algebra indexed by a non-empty set I . Thus,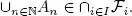

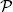 (Ω) . The σ-algebra σ (ε) generated by ε is the intersection of all σ-algebras containing ε . It is the smallest σ-algebra containing ε . ε is called the generating system of the σ-algebra σ ( ε ).
(Ω) . The σ-algebra σ (ε) generated by ε is the intersection of all σ-algebras containing ε . It is the smallest σ-algebra containing ε . ε is called the generating system of the σ-algebra σ ( ε ).
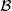 (ℝ) generally denotes the σ-algebra of Borel sets. It must be recalled that this is also the σ-algebra generated by the intervals, or by the intervals of the form ] − ∞ , x ] , x ∈ ℝ . Thus, there is no unicity of the generating system .
(ℝ) generally denotes the σ-algebra of Borel sets. It must be recalled that this is also the σ-algebra generated by the intervals, or by the intervals of the form ] − ∞ , x ] , x ∈ ℝ . Thus, there is no unicity of the generating system .