This book is arranged as follows: Chapter 1reviews the basic concepts and notations in probability and random variables, especially discrete variables, and also provides an introduction to the concept of stochastic processes. Chapter 2is dedicated to the introduction and study of the concept of conditional expectation, a key concept in the definition of martingales and the computation of financial options. Chapter 3aims to introduce an interesting example of stochastic process, namely a simple symmetric random walk, with minimal formalism. This chapter may be read as a standalone chapter. Chapter 4defines and characterizes the concept of a martingale in discrete time and studies certain properties.
From Chapter 5onward, we focus on financial mathematics, strictly speaking. We define essential financial vocabulary such as the concept of a financial asset, investment strategy and the concept of arbitrage. We also begin to establish a link with martingales. We also introduce a typical example of a discrete financial market: the Cox, Ross and Rubinstein binomial model, which acts as a guiding thread through all the following chapters. In particular, the question of Optimal Portfolio Management in this model is studied through guided work. This is a discretized version of the famous Merton problem, originally posed in the continuous Black and Scholes [MER 69] model. Chapter 6introduces and studies the first large and specific category of conditional assets, i.e. European options. This is the simplest example of a financial asset which may be exercised subject to the realization of a certain condition. We examine, in detail, the question of the pricing and hedging of these options in the general case of a discrete financial market and then in the specific case of the Cox, Ross and Rubinstein model. Chapter 7is dedicated to the study of a slightly more complex family of conditional assets: American options. We once again undertake a detailed study of the question of the pricing and hedging of these options and connect them to the theory of optimal stopping, in the general case of a discrete financial market and then in the specific case of the Cox, Ross and Rubinstein model.
The detailed solution to all the exercises and practical work are given together at the end of the book in Chapter 8.
1
Elementary Probabilities and an Introduction to Stochastic Processes
This chapter reviews the basic concepts related to probability and random variables which will be useful for the rest of this text. For a more detailed explanation as well as demonstrations, the readers may refer to [BAR 07, DAC 82, FOA 03, OUV 08, OUV 09] in French and [BIL 12, CHU 01, DUR 10, KAL 02, SHI 00] in English. The readers who are already familiar with these concepts may proceed straight to section 1.3, which introduces the concept of stochastic processes.
This chapter begins with a brief summary of the concepts of a σ -algebra in section 1.1. These concepts will help in understanding the construction of the properties of conditional expectation in Chapter 2. We then study the chief definitions and properties of random variables and their distribution in section 1.2. There is an emphasis on discrete random variables as this entire book essentially studies discrete cases. Section 1.3defines a stochastic process, which is the main subject studied in this book. Finally, there are exercises in handling these different concepts in section 1.4. The solutions are given in Chapter 8.
Throughout the rest of the text, Ω is a non-empty set and 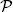 (Ω) denotes the set of the subsets of Ω :
(Ω) denotes the set of the subsets of Ω :
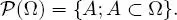
The set Ω is called the universeor the fundamental set. In practice, the set Ω contains all the possible outcomes of a random experiment.
1.1. Measures and σ -algebras
Let us start by reviewing the concept of a σ -algebra.
DEFINITION 1.1.– A subset  of
of 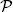 (Ω) is a σ-algebra over Ω if
(Ω) is a σ-algebra over Ω if
1 1) Ω ∈ ;
2 2) is stable by complementarity: for any A ∈ , we have Ac ∈ , where Ac denotes the complement of A in Ω: Ac = Ω\A;
3 3) is stable under a countable union: for any sequence of elements (An)n∈ℕ of , we have
Elements of a σ-algebra are called events .
EXAMPLE 1.1.– The set 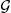 = {∅, Ω} is a σ-algebra and is also the smallest σ-algebra over Ω ; it is called the trivial σ-algebra. Indeed ,
= {∅, Ω} is a σ-algebra and is also the smallest σ-algebra over Ω ; it is called the trivial σ-algebra. Indeed , 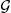 is in fact a σ-algebra since Ω ∈
is in fact a σ-algebra since Ω ∈ 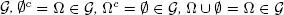 and by creating unions of ∅ and Ω we always obtain ∅ ∈
and by creating unions of ∅ and Ω we always obtain ∅ ∈ 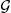 or Ω ∈
or Ω ∈ 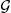 . Further, for any other σ-algebra
. Further, for any other σ-algebra  , we clearly have
, we clearly have 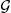 ⊂
⊂  .
.
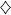
EXAMPLE 1.2.– The set 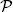 (Ω) is the largest σ-algebra over Ω ; it is called the largest σ-algebra. Indeed, by construction ,
(Ω) is the largest σ-algebra over Ω ; it is called the largest σ-algebra. Indeed, by construction , 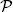 (Ω) contains all the subsets of Ω , and thus it contains in particular Ω and it is stable by complementarity and under countable unions. In addition, any other σ-algebra
(Ω) contains all the subsets of Ω , and thus it contains in particular Ω and it is stable by complementarity and under countable unions. In addition, any other σ-algebra  over Ω is clearly included in
over Ω is clearly included in 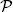 (Ω).
(Ω).
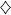
DEFINITION 1.2.– Let Ω be a non-empty set and  be a σ-algebra over Ω . The couple (Ω,
be a σ-algebra over Ω . The couple (Ω,  ) is called a probabilizable space .
) is called a probabilizable space .
Читать дальше

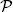 (Ω) denotes the set of the subsets of Ω :
(Ω) denotes the set of the subsets of Ω :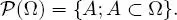
 of
of 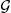 = {∅, Ω} is a σ-algebra and is also the smallest σ-algebra over Ω ; it is called the trivial σ-algebra. Indeed ,
= {∅, Ω} is a σ-algebra and is also the smallest σ-algebra over Ω ; it is called the trivial σ-algebra. Indeed , 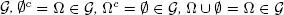 and by creating unions of ∅ and Ω we always obtain ∅ ∈
and by creating unions of ∅ and Ω we always obtain ∅ ∈