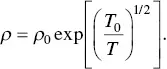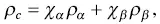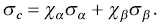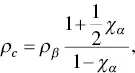1 ...6 7 8 10 11 12 ...15 The temperature dependence of the conductivity of semiconductors is quite different from metals. The temperature can affect both the charge carrier density and the charge carrier mobility of semiconductors. There are three temperature ranges in terms of the temperature effect on the charge carrier density. At the low temperature range below the saturation temperature ( T s), the thermal energy is less than the ionization energy of the doping atoms. As a result, not all the doping atoms ionize. The electron (or hole) density in the conduction band (or valence band) depends on the thermal excitation of the electrons (or holes) from the dopant to the conduction band (or valence band). The charge carrier density increases with the increasing temperature. In the medium temperature of T s< T < T iwith T ibeing the intrinsic temperature, the thermal energy is high enough for the ionization of all the dopants, but it is lower than the energy bandgap between the valence band and the conduction band. The charge carrier density equals the dopant density, and it is constant in this temperature range. At the high temperature range of T > T i, the thermal energy can excite the electrons from the conduction band to the valence band. This produces electrons in the conduction band and holes in the valence band. In this high temperature range, both the electron and hole densities increase with the increasing temperature.
There are two temperature regimes for the temperature dependence of the charge carrier mobility of semiconductors. At low temperature regime, the ionized impurities are the charge carrier scattering centers. In this temperature range, the charge carrier mobility increases with the increasing temperature because the scattering area decreases. At high temperature, the scattering by the lattice vibration becomes the dominant factor for the charge carrier mobility. Similar to metals, the charge carrier mobility decreases with the increasing temperature in the high temperature regime.
Therefore, the temperature dependence of the conductivity of semiconductor is more complicated than that of metals. At low and high temperature range, the conductivity of semiconductor increases with the increasing temperature. The conductivity can be less sensitive to the temperature or even decrease in the medium temperature range.
The temperature dependence of the conductivity is usually used to determine whether a conductor is metallic or semiconductive. In general, if the conductivity decreases with the increasing temperature, it is metallic. In contrast, if the conductivity increases with the increasing temperature, it is considered as semiconductive behavior. This is also frequently used to judge the charge transport mechanism of non‐conventional materials, such as carbon nanotubes, graphene, and charge‐transfer organic salts.
1.1.5.3.3 Conducting Polymers
The temperature dependence of the conductivity of conducting polymers is different because they are disordered systems. The charge transport is dominated by the interchain charge hopping. In general, the conductivity of conducting polymers follows the one‐dimensional variable range hopping model,
(1.17) 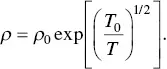
In terms of this model, the resistivity increases with the increasing temperature. The kT 0value suggests the energy barrier for the charge hopping. It decreases with the increasing crystallinity. It is easy to confuse the charge hopping mechanism with the metallic band structure of conducting polymers. At high doping level, the conducting polymers can have energy band structure like metals. This picture is applicable for an individual chain. For a conducting polymer sample, the charge transport is dominated by interchain charge hopping.
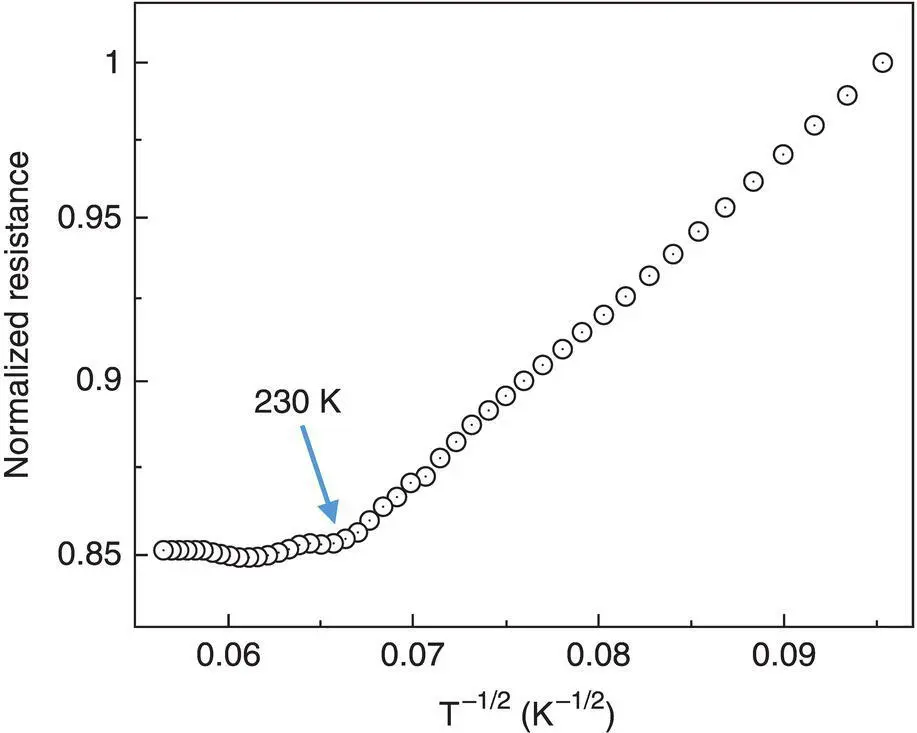
Figure 1.16 Temperature dependence of the resistance of a PEDOT:PSS treated with H 2SO 4.
Source: Xia et al. [21]. © John Wiley & Sons.
However, semimetallic or metallic behavior, that is, the conductivity is insensitive to temperature or decreases with the increasing temperature, was reported on a few conducting polymers with high conductivity. For example, H 2SO 4treatment can enhance the conductivity of a PEDOT:PSS film prepared from the Clevious PH1000 aqueous dispersion from ~0.2 S cm −1to >3000 S cm −1[21]. As shown in Figure 1.16, when the temperature is lower than 230 K, the temperature dependence of the resistance still follows the one‐dimensional variable range hopping model. Nevertheless, when the temperature is higher than 230 K, the thermal energy can overcome the energy barrier for the interchain charge hopping. As a result, the resistance becomes insensitive to temperature. This indicates semimetallic or metallic behavior. Metallic or semimetallic behavior was also observed on highly conductive polyaniline [27].
1.1.5.4 Conductivity of Composites
Some composites particularly the dispersion of inorganic nano‐fillers in polymer matrix can exhibit high thermoelectric properties [28, 29]. There can be three different structures for a two‐phase composite ( Figure 1.17). The resistivity ( ρ c) of the composites depends on the volume fractions and the resistivity of the two phases. When the two phases α and β are in series, the resistivity of the composite is given by,
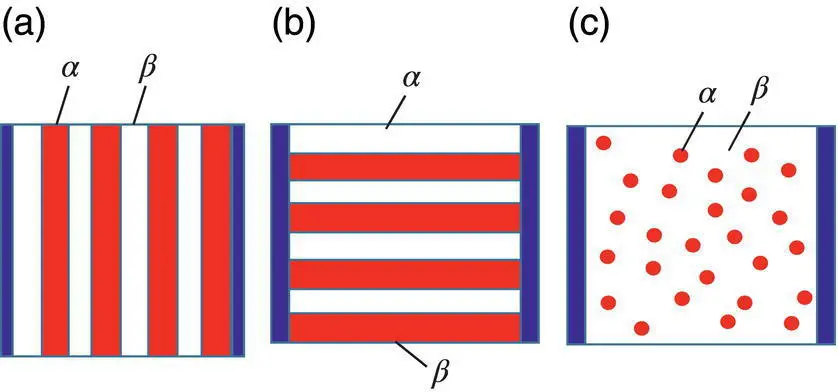
Figure 1.17 Structures of a composite with two phases of α and β (a) in series, (b) in parallel, and (c) one phase dispersed in another phase.
(1.18) 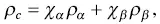
where χ αand χ βare the volume fractions of the α and β phases, respectively, and ρ αand ρ βare the resisitivities of the two phases, respectively. The resistivity of the composite is dominated by the phase of higher resistivity.
When the two phases of α and β are parallel, the conductivity ( σ c) of the composites is related to the conductivities of the two phases by the following equation,
(1.19) 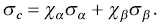
The phase with higher conductivity will be the dominant one for the conductivity of the composite.
If a composite has a structure of the α phase dispersed in the β phase, the α phase is the dispersed phase and the β phase is the matrix. The resistivity of the composite depends on the relative resistivities of the two phases. If the α phase is more resistive than the β phase, ρ α> 10 ρ β, the resistivity of the composite is given by
(1.20) 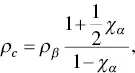
Читать дальше