2 2. Unsupervised Leaning: In unsupervised learning, the algorithm only feeds the set of input to the neural model and the weighted connection of the network is adjusted by internal monitoring system. The neural network finds some kind of pattern within the given input and accordingly the artificial is network is modified without any external assistance.
3 3. Reinforcement Learning: Reinforcement learning has some resemblance with supervised learning, but in this case no target output is given, instead, certain reward or penalties are given based on the performance of the neural model. It is a goal-oriented algorithm which receives the reward through trial-and-error method.
So far, we have given a brief overview of ANNs which a significant domain of artificial intelligence. In the next section, we will focus on the core area of this chapter, i.e., ANN using DNA computing. In the sphere of DNA computation, the logical aspect of artificial intelligence has been replaced by chemical properties and characteristics of DNA molecules.
DNA molecules are capable of storing and processing information which stimulates the idea of DNA computing. It is the emerging arena in the domain of computation, and gradually, we are approaching toward the paradigm shift, from silicon to carbon, where DNA computing is overcoming the drawbacks of traditional silicon-based computing. Because of the unique properties (like, Watson-Crick base pairing) of DNA molecules, it has become an influential tool of engineering at nano-scale. The models of ANNs, DNA logic gates, and DNA logic circuits, as illustrated in this chapter, inspire the basic design of DNA computer.
Set of short DNA sequences, i.e., DNA oligonucleotides can be used to design a model of ANN. These short DNA sequences are used to code input and output signal and to build the basic architecture of the neuron. In the subsequent subsections, we focus on some of the ANN models developed using DNA sequences.
2.4.1 Formation of Axon by DNA Oligonucleotide and Generation of Output Sequence
Mills [4] has developed a simple model of neural network which is capable to transport signal using DNA oligonucleotides. The states of activity of the neural model are coded by the concentrations of the neuron DNA oligonucleotides. The input and output neurons are coded by single stranded DNA sequences. Partially double-stranded DNA sequences denote the formed axons.
The DNA oligonucleotides that represent the input and output signals are used to encode the axon of the neural model. These oligonucleotides are then temporarily attached to each other by a linker oligonucleotide. The one half of the linker sequence is complementary to the half of output neuron oligonucleotide and other half is complementary to the prefix of input neuron oligonucleotide. Then, T4 DNA ligase joins these two oligonucleotides permanently. The polymerase extension of the linker sequence along with the out sequence is used to protect the output end of linked oligonucleotide. The formation of the axon sequence is explained in Figure 2.9. The rate at which input neuron DNA concentrations lead to the generation of corresponding concentration of output neuron oligonucleotides is governed by the concentration of the axon DNA oligonucleotides. Axon of each neuron can be prepared in the form of partially double-stranded DNA sequences in ideal wet lab environment.
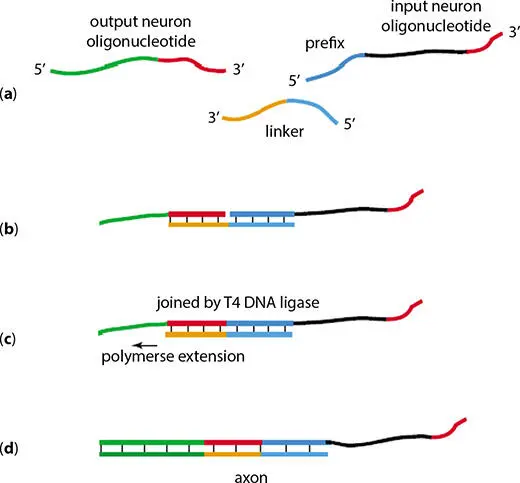
Figure 2.9 Formation of axon. (a) Input and output neuron oligonucleotides and the linker sequence. (b) Input and output neurons get hybridized to each other using the linker sequence. (c) Input and output neurons are joined by T4 DNA ligase; DNA polymerase starts the extension of the linker molecule along the output oligonucleotide. (d) Partially double-stranded axon is formed after completion of polymerase extension.
For development of the model of single-layer neural network, a set of input neuron oligonucleotide, complementary to the input neurons, is used. This set and designed axon sequence ( Figure 2.9) are mixed together. This mixed solution is treated with DNA polymerase in presence of appropriate reaction buffer. The input neuron hybridizes to the single stranded part of partially double-stranded axon. This hybridization procedure releases the output oligonucleotide from the axon molecules that were already attached on their output end. This mechanism is illustrated in Figure 2.10.

Figure 2.10 Formation of output molecule using DNA neural network. (a) Axon molecule and input oligonucleotide. (b) Input molecule hybridizes to the corresponding axon; extension of the strands gets started using DNA polymerase. (c) The extension of the primer leads to the release of output DNA oligonucleotide.
Generalization of the above discussed single-layer neural model to multi-layer networks is possible. To achieve this, each layer should be designed individually. The output of one layer is the input of the following layer in the multi-layer model.
2.4.2 Design Strategy of DNA Perceptron
In 2009, Liu et al . [5] used the property of massive parallelism of DNA molecules and designed a model perceptron. Thus, the running time of the algorithm can be reduced to a great extent. The structure of the perceptron is presented in Figure 2.11. It has two layers: the input layer generates n input signals and the output layer generates m output signals. Apart from n number of input signals, there is another additional signal termed as bias signal. The i thinput neuron is joined with j thoutput neuron by a joining weight denoted as, w ij. Each of the m output neurons receives n signals from the input layer and organizes them with the corresponding n weight coefficient. The weighted sum for each output neuron can be expressed by the following equation;
(2.6) 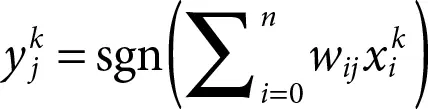
where
k ≡ k thsample of training set;
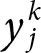 ≡ output value of j thoutput neuron;
≡ output value of j thoutput neuron;
wij ≡ weight value joining i thinput and j thoutput neuron;
 ≡ input value of i thinput neuron.
≡ input value of i thinput neuron.
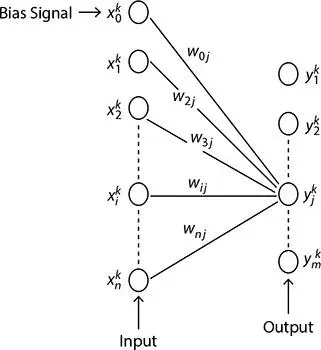
Figure 2.11 Structure of perceptron [5].
The designed algorithm for perceptron categorizer model follows two processes: one is training process and the other is category process.
• Training process: In this process, the ideal input values, , and the ideal output values, , are used to train weight coefficient to get the set of weights. The sample vector is represented by Equation (2.7). (2.7)
The set of weights, wk , is represented by the following expression:
Читать дальше



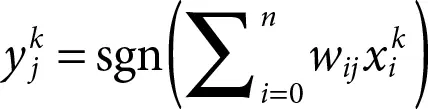
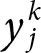 ≡ output value of j thoutput neuron;
≡ output value of j thoutput neuron; ≡ input value of i thinput neuron.
≡ input value of i thinput neuron.











