Tao and Wang (2015) propose a simple TS algorithm for the routing problem and a least waste algorithm for the packing problem.
Junqueira et al . (2013) propose an ILP exact method to solve small-scale instances of the 3L-CVRP (number of customers <15). They assume a homogeneous vehicle fleet, sequence-based loading, stacking constraints, orientation constraints and stability constraints. The authors take into account the unloading pattern of the items at customer sites to be solved.
Hokima et al . (2016) propose two branch-and-cut algorithms for the 3L-CVRP variant with only an LIFO constraint but no fragility and stability constraints. In addition, the authors propose an iterated local search (ILS) method for the routing sub-problem.
Vega et al . (2020) propose a hybrid heuristic that combines a greedy randomized adaptive search procedure (GRASP) heuristic and a Clarke and Wright savings (CWS) algorithm.
1.3.2. Problem description
The 3L-CVRP is defined as follows (Gendreau et al . 2006). Let G = ( V , E ) be a complete graph, where V = {0, 1, …, n} is a set of n + 1 vertices and E the complete set of edges connecting each vertex pair.
Vertex 0 corresponds to the depot, while vertices {1, …, n} are the n customers to be served. Each edge is denoted by ( i , j ) and has an associated routing cost cij where ( i , j = 0, …, n ).
It is also given a fleet of v homogeneous vehicles, each one is characterized by four variants D , W , H and L presented the capacity, the width W , the height H and the length L , respectively. Each vehicle has an opening on the rear for the loading/unloading operations. We suppose the opening to be as large as the vehicle ( W* H ).
The demand of customer i consists of a set of mi items whose total weight is di ( i = 1, …, n ). Each item k of customer i is denoted by Iik and is a 3D cuboid, having width w ik , height hik and length lik ( i = 1, …, n , k = 1, …, mi ).
The total demand asked by a customer i is denoted by 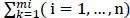 .
.
The 3L-CVRP calls for finding a set of at most v routes where minimizing the total travel cost with ensuring that the constraint 3D of each item is respected. A 3D loading is feasible if it does not exceed the vehicle weight capacity D and if there exists a placement of the items in the vehicle volume that satisfies both the classical 3D-BPP constraints (items do not overlap and are completely contained by the bins/vehicles) and a series of operational constraints. Figure 1.2illustrates an example of 3L-CVRP solution.

Figure 1.2. An example of a 3L-CVRP solution
The most studied 3L-CVRP variants are 3L-CVRP with time windows, 3L-CVRP with backhauls and 3L-CVRP with pickup and delivery. The 3L-CVRP is integrated with 3D-BPP constraints such as last in-first out (LIFO); rotation of items; vertical stability; fragility and weight limit.
1.3.3.1. 3L-CVRP with time windows
Moura (2008) presented three objectives organized as follows, to minimize the number of vehicles and the total distance and to maximize the volume used, respectively. Moura and Oliveira (2009) developed a sequential approach (using LS and GRASP heuristics) and a hierarchical approach (using constructive; post constructive; and local search phase) to solve the 3L-CVRPTW. The objectives are to minimize the number of vehicles and the total route time. In the hierarchical approach, the loading problem is seen as a sub-problem of the routing problem.
Bortfeldt and Homberger (2013) described two steps: the first one is to pack items into vehicles with respect to the capacity of each vehicle and the second one consists of designing a route sequence.
Zhang et al . (2017) proposed a hybrid approach by combining TS and the artificial bee colony (ABC) algorithm to solve a VRP with pallet loading and time window constraints.
The problem considers the LIFO constraint; fragility and orientation are not considered. Moura et al . (2019) presented a MILP model. The model allows all boxes to rotate in 3D and they may also have fixed or limited orientation. The boxes could be loaded in multiple layers formed by different sized and shaped boxes.
Vega et al . (2019) studied VRP with 3D loading constraints and additional constraints such as time windows and capacity constraints. They proposed a nonlinear mixed integer program (NLMIP). Pace et al . (2015) considered a constraint of a heterogeneous fleet of vehicles for the 3L-CVRPTW. Iterated local search (ILS) and simulated annealing (SA) are proposed to solve the problem.
1.3.3.2. 3L-CVRP with backhaul
The combination of VRP with backhauls and loading constraints is a recently studied problem. Bortfeldt et al . (2015) proposed a large neighborhood search and a variable neighborhood search (LNS-VNS) for solving the 3D VRP with backhaul in both routing and a packing procedure in addition, a tree search heuristic (TSH) is considered for loading items. Koch et al . (2018) addressed the CVRP with time windows and 3D loading constraints (3L-VRPSDPTW). They used a large neighborhood search to solve the problem. Reil et al . (2018) extended the last approach proposed by Bortfeldt et al . (2015) for the VRPBTW with 3D loading constraints by considering various types of backhauls. Koch et al . (2020) proposed a TS for the routing problem and a set of loading heuristics for the loading problem for solving the 3L-CVRP with mixed backhauls (3L-VRPMB).
1.3.3.3. 3L-CVRP with pickup and delivery
Bartok and Imreh (2011) used a simple local search method for solving the 3L-VRPPD. Mannel and Bortfeldt (2016) discussed several 3L-VRPPD variants and hybrid approaches based on LNS and tree search heuristics are proposed for packing boxes.
1.3.3.4. 3L-CVRP with split delivery
Yi and Bortfeldt (2016) addressed the 3L-SDVRP with the same packing constraints as the 3L-CVRP in Gendreau formulation. Only inevitable splits are allowed, that is serving a customer in two or more routes is only permitted if not all boxes can be packed into a single loading space. A hybrid heuristic is developed that can be considered as a preliminary variant of the algorithm presented here.
Li et al . (2018) proposed a novel data-driven three-layer search algorithm to solve the 3L-SDVRP. They minimize the number of vehicles used as a first priority and the total travel distance as a second priority.
Bortfeldt and Yi (2020) studied two variants of the 3L-SDVRP. In the first, a delivery is only split if the customer demand cannot be carried by a single vehicle. In the second, splitting customer deliveries can be done any number of times. The authors proposed a hybrid algorithm consisting of an LS and a GA to solve the two variants.
Table 1.2presents a comparative study of the existing literature on 3L-CVRP.
Читать дальше

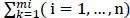 .
.











