In recent years, some researchers have focused on the combined routing and loading problem. The combinatorial problem includes the 2D loading VRP, denoted as 2L-CVRP and the 3D loading VRP, denoted as 3L-CVRP. The purpose of addressing these problems is to minimize the overall travel costs associated with all the routes that serve each of the customers, as well as to satisfy all the constraints of the loading dimensions. The two problems are solved by exact and metaheuristic algorithms which are reviewed in detail in the sections that follow. For further information, we refer the reader to Pollaris et al . (2015) and Iori and Martello (2010), wherein detailed surveys are presented in relation to vehicle routing with packing problems.
This chapter is organized as follows: section 1.2provides an overview of the literature concerning VRPs in combination with 2D loading problems and the existing variants and constraints. Section 1.3focuses on VRPs with 3D loading problems and the existing variants and constraints. Finally, in section 1.4, we close with conclusions and opportunities for further research.
1.2. The capacitated vehicle routing problem with two-dimensional loading constraints
The 2L-CVRP is a variant of the classical CVRP characterized by the two-dimensionality of customer demand. The problem aims to serve a set of customers using a homogeneous fleet of vehicles with minimum total cost. The 2D loading constraints must be respected.
The 2L-CVRP is available in a set of real-life problems (Sbai et al . 2020b), for example household appliances and professional cleaning equipment. Table 1.1presents a comparative study of the existing literature for the 2L-CVRP, which includes solution methods, variants and constraints.
Table 1.1. Comparative study of the 2L-CVRP
| Author |
Problem |
Routing problem Solution methods |
Loading problem Solution methods |
| lori et al . (2007) Gendreau et al . (2008) Fuellerer et al . (2009) Zachariadis et al . (2009) |
2L-CVRP 2L-CVRP 2L-CVRP 2L-CVRP |
Branch-and-cut TS ACO GTS |
Branch-and-bound LH2SL, LH2U L LB, Branch and Bound Bottom-Left Fill (L,W axis) Max Touching Perimeter Max Touching Perimeter No Walls Min Area Bottom-Left Fill(L,W axis) Max Touching Perimeter Max Touching Perimeter No Walls Min. Area LBFH GRASP-ELS PRMP |
| Leung et al . (2011) |
2L-CVRP |
EGTS |
| Duhamel et al . (2011) Zachariadis et al . (2013) Wei et al . (2015) Wei et al . (2017) Sbai et al . (2020b) Leung et al . (2013) |
2L-CVRP 2L-CVRP 2L-CVRP 2L-CVRP 2L-CVRP 2L-HFVRP |
GRASP-ELS LS VNS SA GA SA H LS |
Skyline heuristic Open space based heuristic ALWF Bottom-Left Fill (L,W axis) Max. Touching Perimeter Max. Touching Perimeter No Walls Min. Area Max. fitness value Bottom-Left Fill (L,W axis) Max Touching Perimeter Max. Touching Perimeter No Walls Min. Area Max. fitness value Lower Bound L-cuts MA ALWF ILP GVNS BLH Best-Fit LS VNS VNS LS Bottom-Left Heuristics |
| Sabar et al . (2020) |
2L-HFVRP |
MA |
| Cote et al . (2013) Cote et al . (2020) Khebbache-Hadji et al . (2013) Sbai et al . (2017) Attanasio et al . (2007) Song et al . (2019) Pinto et al . (2015) Dominguez et al . (2016) Zachariadis et al . (2017) Pinto et al . (2017) Pinto et al . (2020) Zachariadis et al . (2016) Malapert et al . (2008) |
S2L-CVRP S2L-CVRP 2L-CVRPTW 2L-CVRPTW 2L-CVRPTW 2L-CVRPTW 2L-VRPMB 2L-VRPB 2L-VRPB 2L-SPD 2L-VRPB 2L-VRPMB 2L-SPD 2L-VRPPD |
L-Cuts L-Cuts MA GA ILP GVNS Insert-heur LNS Touch-Per LS VNS VNS LS Scheduling based-model |
The 2L-CVRP is an NP-hard problem, it is solved by exact, heuristic and metaheuristic algorithms:
Iori et al . (2007) use the first exact algorithm for solving small-scale instances of the 2L-CVRP and only for the sequential variant. They proposed a branch-and-cut approach for the routing problem and branch-and-bound for the packing problem.
Gendreau et al . (2008) use a Tabu search (TS) metaheuristic algorithm. They considered two loading heuristics for the sequential and unrestricted case, known as the LH2S L and the LH2U L.
Zachariadis et al . (2009) propose another metaheuristic algorithm which integrates TS and guided local search, referred to as GTS. For the loading problem, they used five packing heuristics and three neighborhood searches to generate the initial solution, namely: customer relocation, route exchange and route interchange.
Fuellerer et al . (2009) present an algorithm based on ant colony optimization (ACO) while bottom-left-fill and touching perimeter algorithms are proposed for solving the packing problem.
Leung et al . (2011) propose an extended guided Tabu search (EGTS) algorithm for the routing problem and a lowest line best-fit heuristic (LBFH) to solve 2D-BPP.
Duhamel et al . (2011) use the greedy randomized adaptive search procedure and the evolutionary local search algorithm, denoted GRASP-ELS.
Leung et al . (2013) study the heterogeneous fleet vehicle routing problem (2L-HFVRP). They propose six packing heuristics to check the feasibility of loading (presented in Table 1.1) and simulated annealing with a heuristic local search (SA-HLS) for the routing problem.
Zacharidis et al . (2013) present a static move description algorithm.
Dominguez et al . (2016) study the 2L-CVRP with a heterogeneous fleet using the multi-start biased randomized algorithm and the touching perimeter algorithm for the packing problem.
Wei et al . (2015) propose a variable neighborhood search (VNS) approach for solving the 2L-CVRP and adapt the skyline heuristic to examine loading constraints.
Wei et al . (2017) propose the simulated annealing (SA) algorithm to solve 2 |SO| L, 2 |SR| L, 2 |UO| L and 2 |UR| L versions of the 2L-CVRP.
Sbai et al . (2017) propose a new heuristic based on an adaptive genetic algorithm (GA) for solving the 2L-CVRP, considering only the unrestricted loading case.
Sabar et al . (2020) present a heterogeneous fleet 2L-CVRP, denoted as 2L-HFVRP. They propose a two-stage method: the routing stage and the packing stage. The problem is solved using MA for the routing stage and five heuristics (presented in Table 1.1) for the packing stage.
Coté et al . (2020) introduce a stochastic variant of the 2L-CVRP, known as the S2L-CVRP, where the size of some items is uncertain at the time the vehicle routes are planned. They use a lower bounding functional, called L-cuts, to solve the problem.
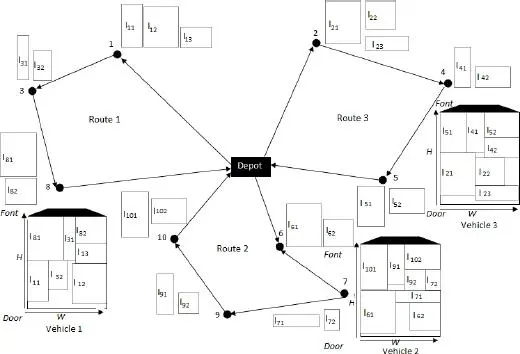
Figure 1.1. An example of a 2L-CVRP solution
1.2.2. Problem description
2L-CVRP is defined (Gendreau et al . 2008) on a complete undirected graph G = ( V , E ), where V = {0, …, n } is the vertex set and E = { ( i , j )| i , j ϵ V , i ≠ j } is the edge set characterized by a cost c i j. A set of v homogeneous vehicles are located at the depot, each one is identified by D , W and H representing the weight capacity, the width and the height, respectively. Let A = W *H denote the loading area. The demand of client i {1, …, n} consists of mi items of total weight di : item Iil { l =1, …, mi } has width wil and height hil . Let ai = 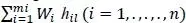 denotes the total area of the client i demand. Figure 1.1illustrates an example of 2L-CVRP solution.
denotes the total area of the client i demand. Figure 1.1illustrates an example of 2L-CVRP solution.
Читать дальше


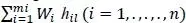 denotes the total area of the client i demand. Figure 1.1illustrates an example of 2L-CVRP solution.
denotes the total area of the client i demand. Figure 1.1illustrates an example of 2L-CVRP solution.










