Paul J. van Leeuwen - Quantum Physics is NOT Weird

Albert Michelson received the Nobel Prize in physics in 1907 for his performance in optics and his contribution to physics. A considerable prize for a "failed" experiment.

The subject of the previous paragraphs was the rise and the great success of classical physics. It has now hopefully become clear why, apart from a few imperfections, classical physics fits so seamlessly into our daily experience of material reality. We can summarize our own everyday experience of the world as follows:

If I want to move something, I must push it or pull it.

What I perceive exists objectively and independently of me. The world seems to exist with or without me.

Even when I am not looking at the moon, or when it has disappeared behind the horizon, I am sure that it is still 100% materially there.

According to classical physics, my inner experience of reality is an image that coincides with the "real" world around me.

Mathematics is the ultimate tool to create a model of the world that explains exactly how it works.

Causality, cause and effect, reigns absolute.

The whole is just the sum of the parts. After analyzing the parts first, in principle the whole is known.

In short, the world seems to us solid and permanent. Most scientists considered physics as virtually complete in the second half of the 19th century, except for a few problems. Smart young students like Max Planck were discouraged from pursuing a career in physics, because there would be no longer any honor to be gained in it. However, it would turn out utterly different.

In 1886, seven years after Maxwell’s publication, Heinrich Hertz(1857-1894) confirmed the existence of standing electromagnetic (radio) waves with a wavelength of almost 61 meters (200 ft). It is probably not a coincidence that the depth of his laboratory was 30 meters, so that half that wavelength fitted precisely. Maxwell's theory was confirmed. Hertz saw no practical use for his discovery. Guglielmo Marconi(1874-1937) saw its potential and realized the first radio communication in 1889. In 1896, shortly after that, the telegram service and the Morse code were invented. Nikola Tesla(1856-1943) forgot to patent his invention concerning sound communication using radio waves and the patent was granted to the cunning Marconi.

In 1895, Wilhelm Röntgen(1845-1923) discovered highly energetic EM-waves generated by applying a high voltage between the electrodes of a vacuum tube. Röntgen called his discovery X-rays.

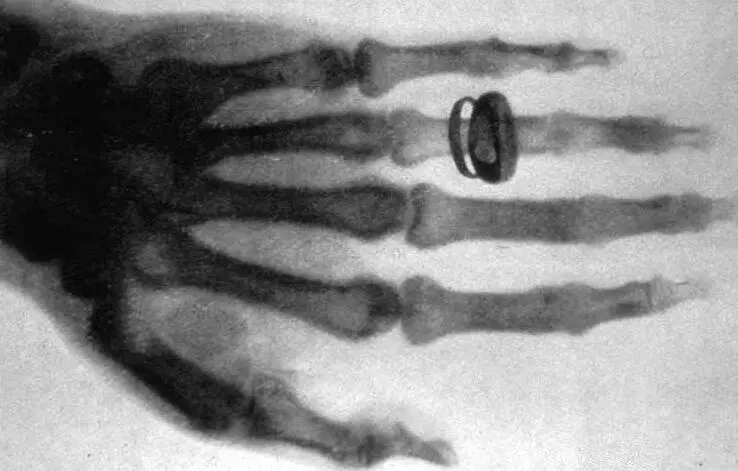
Figure 3.10: Albert von Kölliker’s hand photographed by Röntgen.

These X-rays have wavelengths between 0.01 and 10 nanometers. The first X-ray photos are those of Röntgen’s acquaintances; see figure 3.10 for an X-ray of Albert von Kölliker’s hand. Röntgen also took such an X-ray of his wife's hand. Upon seeing the photo, she feared her end was near. Incidentally, it is a remarkable example of serendipity that Röntgen made his discovery because it struck him that a screen, covered with barium platinocyanide, lit up in his darkened laboratory when he activated his vacuum device. The fact that he had coincidentally such a screen standing readily available in his laboratory, the fact that Röntgen noticed the effect and the fact that he draw the right conclusion is an excellent example of serendipity, the accidental and unsolicited discovery [1 3 ]. Serendipitous discoveries abound in the history of science.

Physicists thus gradually discovered the entire spectrum of EM radiation, from radio waves with wavelengths of thousands of kilometers to gamma radiation with wavelengths of 10 -14meters. Visible light is only a very small part of the full known spectrum. The limits left and right of the spectrum in figure 3.11 are not the limits of EM radiation. There is no known absolute upper or lower limit of the EM spectrum.

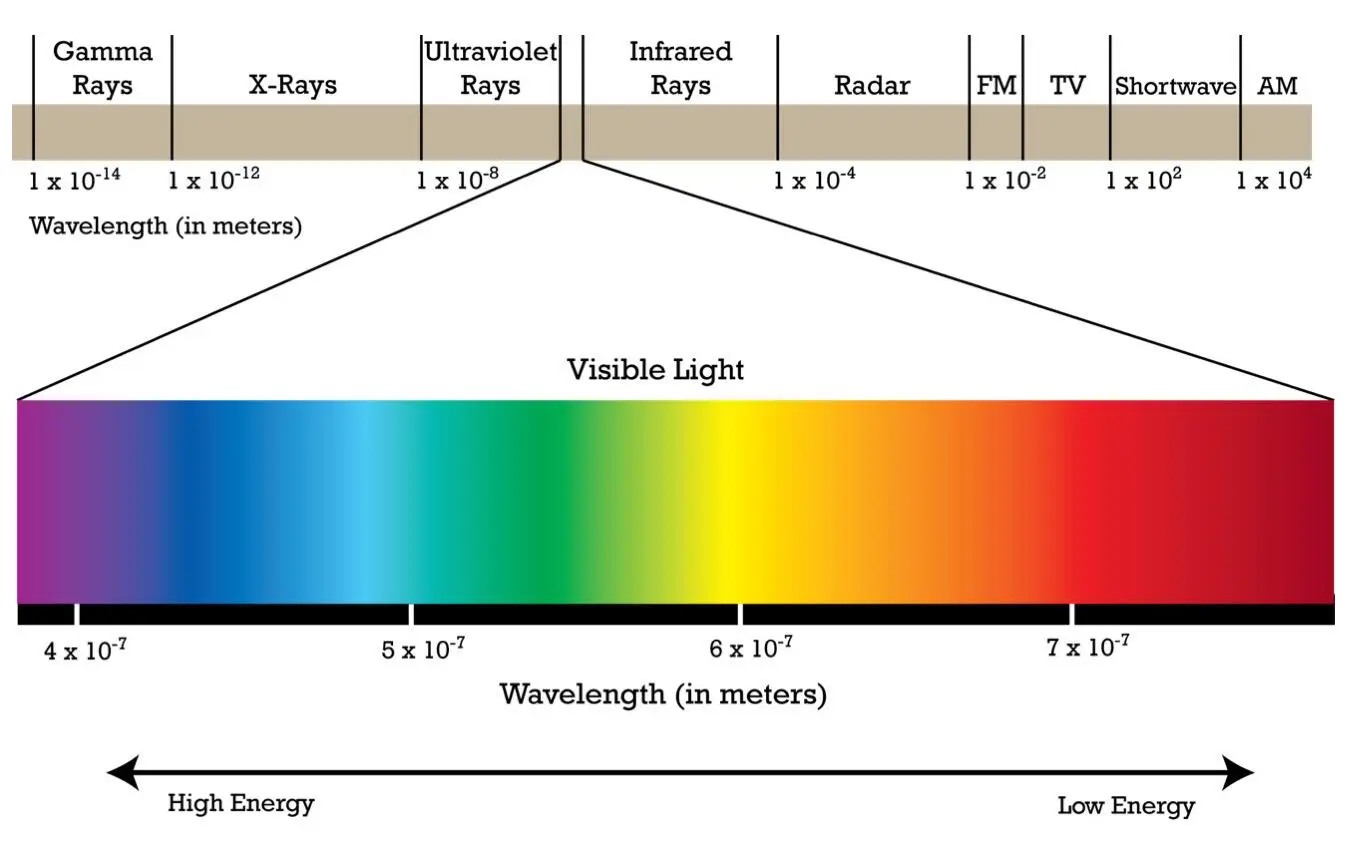
Figure 3.11: The EM-spectrum. Source: biology.stackexchange.com

To the left of the gamma radiation and to the right of the radio waves the EM-spectrum continues infinitely. The limits in figure 3.11 are not fundamental, they represent just the limits of our measuring instruments.

By the time of the rise of electric power, towards the end of the 19th century, the question of what was more efficient, gas light or electric light, became economically important. To investigate their efficiency scientifically, it was necessary to develop a standard light source with which various types of light sources could be compared. In 1887, inspired by Werner von Siemens, a special state laboratory was established in Berlin – the Physikalische-Technische Reichsanstalt – for physical research on applications of electricity and electromagnetic radiation.

The standard instrument for light intensity and color measurement, is basically a closed hollow cavity where the inner walls are heated to a precisely known temperature. The hot inner walls will start to emit and absorb heat radiation – infrared. On further increasing of the temperature, visible light and even UV – ultraviolet light will be emitted.

The intensity distribution of the emitted light, which is an EM-wave spectrum, depends solely on the inside temperature of the walls. Since the cavity is closed the radiation cannot leave it, resulting in an equilibrium condition within the cavity.

In 1859 Gustav Kirchhoff [1 4 ](1824-1887) established, based on theoretical grounds, that the intensity distribution over the EM spectrum of the radiation in that cavity does not depend on the nature of the material of the inner walls, but solely on their temperature. This independency of the construction material is highly suitable for the manufacture of an industry standard for light measurement.

To observe the radiation intensity in the cavity, a small opening– small enough to interfere not with the equilibrium within – is made in the cavity wall. Such a hot EM emitting device in equilibrium is called a Black Body Emitter. It emits Black Body Radiation [1 5 ]. A Black Body is a theoretical device, which absorbs all EM radiation perfectly, so it would be perceived as an utterly black object. It had already become possible, at the end of the 19 thcentury, to compare the light output of different light sources very accurately with these Black Body Emitter devices. Edison's incandescent light bulbs came out as slightly more efficient than those of his competitor Siemens.

Physicists prefer – understandably – mathematical theories with which the behavior of physical systems can be predicted as precisely as possible from fundamental properties of nature. Firstly, this is a confirmation of the theory, secondly, it reduces the number of constants that physics requires for its models, and thirdly, the cost of a pen and paper exercise is considerably less than a real physical experiment.

Max Planck [1 6 ](1858-1947), who had become in 1889 professor at the Friedrichs-Wilhems Universität in Berlin, had been commissioned by Siemens to do theoretical research on maximizing the light intensity from lightbulbs while minimizing energy. At the Physikalische-Technische Reichsanstalt he worked hard to find a theoretical solution for a problem that was known as the UV catastrophe. Statistical calculations in theoretical physics – based on the Maxwell equations for EM radiation – on the emission spectrum of a black emitter resulted in a ‘catastrophic’ prediction. The prediction of the theory was, that a black emitter, heated to 5000 Kelvin ( oK) – this is 5000 degrees above absolute zero – would emit almost all its energy as UV radiation. Just lighting a candle would cause you sunburn but would produce almost no visible light. Fortunately, reality was different. Which was, of course, a challenge for physics. Another theoretical approach of Black Body radiation predicted the emission in the UV range somewhat better but got out of hand in the infrared range. Both classical theoretical approaches misfired spectacularly.