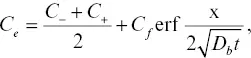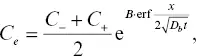2.5.3. Comparison to Previous Studies
It was shown previously that β factors correlate with the diffusivity of the cation normalized by that of Si (or SiO 2) ( Fig. 2.8). Since Si is strongly bound in multi‐atom complexes with O (as well as Al and other Si atoms), it diffuses more slowly than other elements, and hence the ratio D i/ D Siis generally greater than unity. For elements present in major quantities, the ratio D i/ D Siis typically close to unity because of the cooperative motion that is required to yield a net flux of counter‐diffusing major elements. The regime where D i/ D Siis high tends to occur in more silica‐rich liquids and with decreasing temperature (Dingwell, 1990).
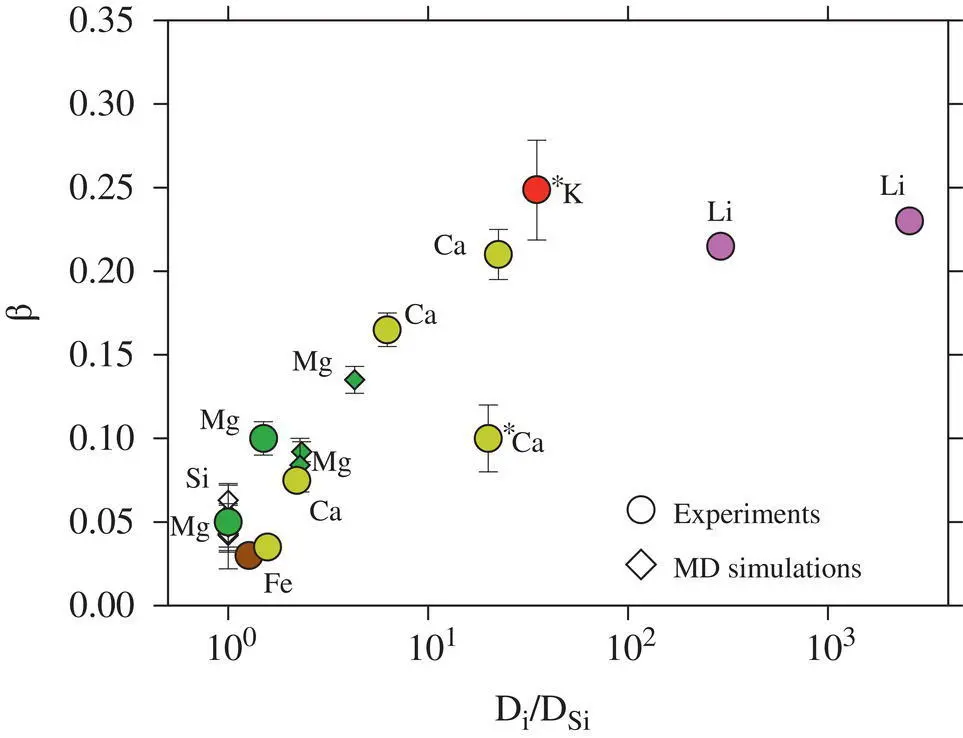
Figure 2.8 β factors from this study (points with an asterisk) compared to literature values. The quantity 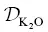 /D Siis used as a proxy for extent to which a diffusing cation is coupled to the melt matrix. The Ca β factor is offset from the overall trend, but this may be because
/D Siis used as a proxy for extent to which a diffusing cation is coupled to the melt matrix. The Ca β factor is offset from the overall trend, but this may be because 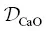 is overestimated. The β factor for K is the largest value yet reported for diffusion in silicate liquids.
is overestimated. The β factor for K is the largest value yet reported for diffusion in silicate liquids.
The ratio 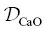 / D Siis inferred to be about 20, and the β factor for Ca is offset from the overall trend. The ratio
/ D Siis inferred to be about 20, and the β factor for Ca is offset from the overall trend. The ratio 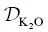 / D Siis inferred to be about 35 and the β factor for K is the highest value yet determined for diffusion in silicate liquids. Despite K 2O being present in major quantities, it behaves like a trace element insofar as its diffusion is kinetically decoupled from the motion of the slower‐moving aluminosilicate structures (cf. Dingwell, 1990). The high β factor suggests that large diffusive isotope effects can arise in high‐ T environments and our results should aid in the search for, and interpretation of, potentially large kinetic K isotope effects in nature.
/ D Siis inferred to be about 35 and the β factor for K is the highest value yet determined for diffusion in silicate liquids. Despite K 2O being present in major quantities, it behaves like a trace element insofar as its diffusion is kinetically decoupled from the motion of the slower‐moving aluminosilicate structures (cf. Dingwell, 1990). The high β factor suggests that large diffusive isotope effects can arise in high‐ T environments and our results should aid in the search for, and interpretation of, potentially large kinetic K isotope effects in nature.
2.6. CONCLUSIONS AND POSSIBLE FUTURE APPLICATIONS
We performed a set of diffusion couple experiments involving unusual phonolite and rhyolite compositions. The data and analysis of those experiments presented here provides additional β factors needed for modeling reaction and transport processes in high temperature geologic systems. Despite the complicated nature of the diffusion profiles, which is an inevitability when dealing with natural silicate liquid compositions, we showed how one can extract a meaningful β factor from the diffusion profiles using a modified effective binary diffusion model that was first developed by Zhang (1993). Our results confirm that β factors vary depending on the element as well as liquid composition, and also that large diffusive isotope effects can arise even in the absence of a large initial concentration gradient. The retrieved β factor for Ca is typical of Ca in natural silicate liquids whereas the β factor for K is the highest value yet reported, suggesting that large diffusive K isotope effects may yet be found in high‐ T environments.
One of the goals of this type of experimental study is to use the growing compilation of β factors to better understand how the mobility of key chemical constituents is controlled, and how that mobility relates to isotopic fractionation of Ca, Mg, Fe, Si, and K in high temperature systems. Recent work shows how isotopic effects in these elements can be used as tracers of micro‐ and nano‐scale processes at mineral surfaces and transport within geologic media at larger scales. For example, Antonelli et al. (2019a) documented small Ca isotope fractionations between volcanic phenocrysts (plagioclase, clinopyroxene, hornblende, and olivine) of various sizes (mm to cm) in lavas ranging in composition from alkali basalt to rhyodacite. They interpreted the effects as being due to diffusive isotope fractionation during crystal growth superimposed on small equilibrium fractionation effects. With knowledge of β factors, they used the model of Watson and Müller (2009) to show how Ca isotope fractionation could be used as a measure of crystal growth rates. They inferred plagioclase growth rates of order 0.03 to 0.3 cm/yr, which is in broad agreement with other estimates of typical volcanic phenocryst growth rates. This approach can be extended to other K‐bearing minerals (e.g., K‐spar, muscovite) using K isotopes in lieu of Ca isotopes.
Another example is the study by Chopra et al. (2012), who used their knowledge of Mg isotope fractionation effects to evaluate the isotopic gradients at the boundaries of a pillowed mafic dike intruded into a granitic intrusion at Vinalhaven, Maine. They used the isotope effects to confirm that diffusion was responsible for the chemical gradients and estimated a diffusion timescale for cooling of the dike‐granite system. We envision extending this to other elements (Ca and K) and other sites. There are many field localities where a mafic (gabbroic) magma with 6–8% CaO and < 1% K 2O has intruded a more silicic (granitic) body with 1–2% CaO and 2–5% K 2O. The Ca concentration gradient is downward toward the granitic phase and the K concentration gradient is downward toward the gabbroic phase. We anticipate that the use of two or more isotopic systems, such as Ca and K, with different temperature‐dependent diffusivities could provide unique information on mixing and cooling processes in magmatic systems.
APPENDIX LINEAR VERSUS EXPONENTIAL DEPENDENCE OF ACTIVITY ON SIO 2
Here we show that the model outputs and conclusions are not dependent on whether the activity is linearly or exponentially dependent on SiO 2concentration. If the activity is an exponential function of SiO 2, then the equation for C e
(2.A1) 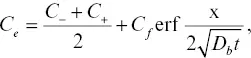
becomes
(2.A2) 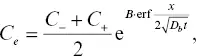
where the parameter B is functionally similar to the parameter C f(Zhang, 1993). An exponential dependence was also adopted by Richter (1993). Fig. 2.9compares the two approaches side by side and shows that the results and conclusions are not sensitive to this particular aspect of the Zhang model.
We are grateful for constructive reviews by James Van Orman and an anonymous reviewer. The experimental work of JMW was supported primarily by the National Science Foundation under Grant Nos. EAR0838168 and EAR0608885 to DJD. Support for isotopic analysis was also provided by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DEAC02‐05CH11231. This work was partially performed under the auspices of the U.S. Department of Energy by the University of California, Lawrence Livermore National Laboratory, under Contract Nos. W‐7405‐ Eng‐48, DE‐AC52‐07NA27344, and DE‐AC02‐05CH1123.
Читать дальше


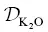 /D Siis used as a proxy for extent to which a diffusing cation is coupled to the melt matrix. The Ca β factor is offset from the overall trend, but this may be because
/D Siis used as a proxy for extent to which a diffusing cation is coupled to the melt matrix. The Ca β factor is offset from the overall trend, but this may be because 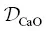 is overestimated. The β factor for K is the largest value yet reported for diffusion in silicate liquids.
is overestimated. The β factor for K is the largest value yet reported for diffusion in silicate liquids.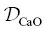 / D Siis inferred to be about 20, and the β factor for Ca is offset from the overall trend. The ratio
/ D Siis inferred to be about 20, and the β factor for Ca is offset from the overall trend. The ratio 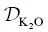 / D Siis inferred to be about 35 and the β factor for K is the highest value yet determined for diffusion in silicate liquids. Despite K 2O being present in major quantities, it behaves like a trace element insofar as its diffusion is kinetically decoupled from the motion of the slower‐moving aluminosilicate structures (cf. Dingwell, 1990). The high β factor suggests that large diffusive isotope effects can arise in high‐ T environments and our results should aid in the search for, and interpretation of, potentially large kinetic K isotope effects in nature.
/ D Siis inferred to be about 35 and the β factor for K is the highest value yet determined for diffusion in silicate liquids. Despite K 2O being present in major quantities, it behaves like a trace element insofar as its diffusion is kinetically decoupled from the motion of the slower‐moving aluminosilicate structures (cf. Dingwell, 1990). The high β factor suggests that large diffusive isotope effects can arise in high‐ T environments and our results should aid in the search for, and interpretation of, potentially large kinetic K isotope effects in nature.