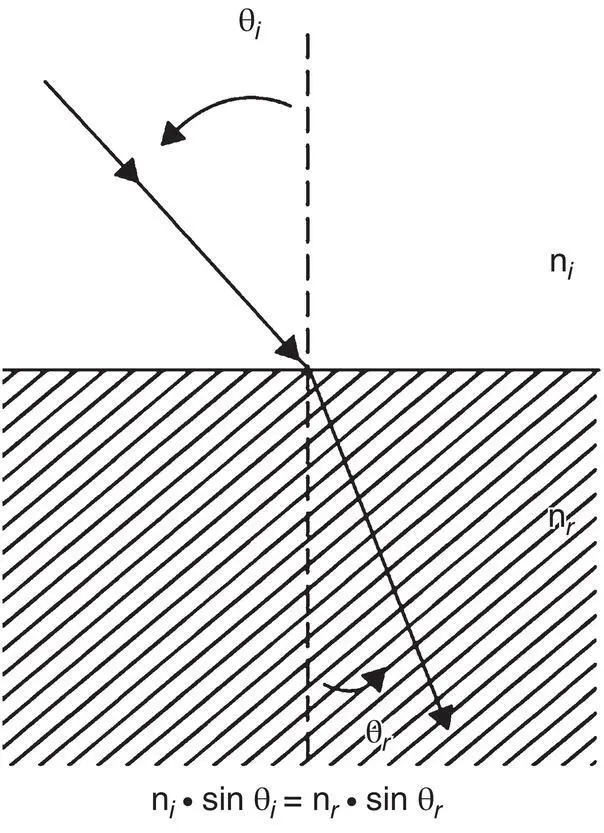
Figure 2.9 Refraction of light as it passes from one medium to another is governed by Snell's law, summarized in the formula below the diagram. The angle of refraction ( θ r) is a function of the angle of incidence ( θ i) and the refractive indices of the two media. In this representation, n i< n r; therefore, θ i> θ r.
Visual Optics
Refractive Structures of the Eye
Precorneal Tear Film and Cornea
As mentioned, light is successively refracted by the various ocular structures as it passes through the eye on its way to the retina. Table 2.13lists the refractive indices and powers of various ocular surfaces in humans. The most anterior optical surface of the eye is the PTF. By strict definition, it could be argued that the tear film is the most refractive layer of the eye. This is due to the large difference in refractive indices as light passes from air, which has a refractive index of almost 1, into the tear film, which has a refractive index of 1.337.
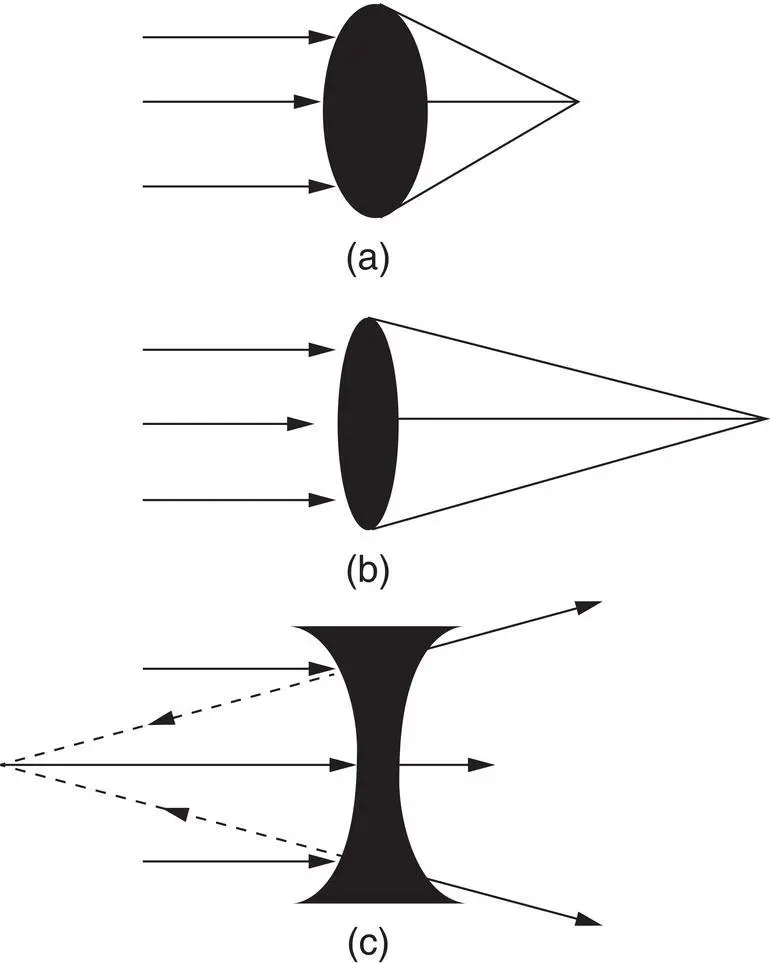
Figure 2.10 Refraction of light through various lenses. (a) A spherical convex lens with a power of 10 D focuses parallel light rays at a distance of 0.1 m. (b) A flatter, less spherical convex lens with a power of 5 D focuses parallel rays at a distance of 0.2 m. (c) Parallel rays passing through a concave spherical lens diverge. A virtual image is formed by tracing back (dashed lines) the diverging rays.
The cornea is the next tissue through which incoming light passes. The human corneal stroma has a refractive index of 1.376. Because this value is slightly higher than the refractive index of the tear film, passage of light from the tear film into the anterior layers of the cornea results in an additional 5 D of refractive power. However, these 5 D are “lost” when light passes from the posterior cornea into the AH, which has a refractive index nearly identical to that of the tears. When combined, the PTF and the cornea of humans contribute a net refractive power of 43 D.
Another factor affecting the refractive power of the cornea, besides the refractive index, is its curvature. Because the cornea converges light, it acts as a convex lens. As stated earlier, the refractive power of such a lens depends to a large extent on its curvature radius. Therefore, in large eyes, which are characterized by flat corneas, the refractive power of the cornea is reduced. Conversely, in small eyes with spherical corneas, its power is increased.
Table 2.13 Refraction constants in the human eye.
| Structure |
Refractive index |
Refractive power (D) |
Reference |
| Tears |
1.336 |
43.0 a |
Montes‐Mico et al. (2004) |
| Cornea |
1.376 |
42.3 a |
Duke‐Elder (1970); Naeser et al. (2016) |
| Anterior surface |
1.401 |
48.2 |
Patel et al. (1995) |
| Posterior surface |
1.373 |
−5.9 |
Patel et al. (1995) |
| Lens |
1.41 |
21.9 |
Duke‐Elder (1970); Chang et al. (2017) |
| Anterior surface |
|
8.4 |
Millodot (1982) |
| Posterior surface |
|
14.0 |
Millodot (1982) |
| Vitreous/aqueous |
1.336 |
|
Duke‐Elder (1970) |
| Retina |
1.363 |
|
Millodot (1982) |
aThe refractive power of the cornea and tears is not additive. Rather, that of the former arises from the latter, and from its interface with air. The net power of the tears and the anterior and posterior cornea is 43 D.
As noted, the refraction that occurs as light passes from the cornea into the AH and during its passage through the aqueous has little overall significance. Therefore, the next significant refractive structure through which light passes after the cornea is the lens. As in the case of the cornea, the refractive power of the lens is determined by both its refractive index and its curvature. In humans and in many nonaquatic species, the refractive index of the lens nucleus is about 1.41; it decreases gradually toward the cortex, forming a bell‐shaped refractive index curve known as the gradient index . In humans, the calculated refractive power of the lens is approximately 22 D.
The second factor determining lenticular refractivity, the lens curvature, also differs between aquatic and nonaquatic species. Generally, it can be said that the lens is spherical in fish and aquatic mammals, while it is more discoid (i.e., less spherical) in terrestrial species. Therefore, the lens will have a higher refractive power in the former compared to the latter ( Table 2.14). The reason for the increased refractive index and lens curvature in aquatic species is the loss of corneal refractive power underwater. Of course, the curvature (and, hence, the refractive power) of the lens can also be changed actively through a process termed accommodation .
The next refractive tissue is the vitreous. Though there is little refraction as light passes from the lens into the vitreous (due to their similar refractive indices), the vitreous plays an important role in refractive development of the eye. Vitreous elongation increases the axial length of the eye, thereby increasing the refractive path of light and inducing myopia, or nearsightedness ( Figure 2.11). In certain fish, this mechanism serves to increase ocular refraction and compensate for loss of corneal refractive power. In different goldfish strains, for example, the vitreous body can contribute anywhere from 37% to 70% of the total axial length of the eye.
Table 2.14 Eye size (ascending order) and corneal power (descending order) in selected animal species.
| Species |
Axial length (mm) |
Corneal power (D) |
References |
| Goldfish |
4.2 |
129 (in air) |
Hughes (1977) |
| Rat |
6.3 |
112.7 |
Hughes (1977) |
| Chicken |
8.9 |
108 |
Cohen et al. (2008) |
| Guinea pig |
8.9 |
83.9 |
Howlett & McFadden (2007) |
| Sea otter |
14.0 |
59.2 |
Murphy et al. (1990) |
| Rhesus monkey (4 months) |
16.3 |
56 |
Qiao‐Grider et al. (2010) |
| Rabbit |
18.0 |
44.6 |
Hughes (1977); Wang et al. (2014) |
| Cat |
21.3 |
43.0 |
Habib et al. (1995) |
| Dog |
19.5–21.9 |
37.8–43.2 a |
Gaiddon et al. (1991); Nelms et al. (1994); Rosolen et al. (1995) |
| Ostrich |
38/0 |
25.3 |
Martin et al. (2001) |
| Elephant |
38.8 |
21.3 |
Murphy et al. (1992a) |
| Horse |
39.2 |
16.5 |
McMullen & Gilger (2006) |
|
43.7 |
15.7–19.5 |
Farrall & Handscombe (1990); Miller & Murphy (2017) |
aThe range of values in the dog probably reflects a breed difference, because larger breeds have flatter corneas.
Accommodation is a rapid change in the refractive power of the eye, which is intended to bring the images of objects at different distances into focus on the retina. The stimulus for the accommodative response is a blurred, or defocused, retinal image. In vertebrates, eyes accommodate by one or more of the following mechanisms: (i) changing the curvature or position of the lens; (ii) changing the corneal curvature; (iii) changing the distance between the cornea and retina; or (iv) having two or more separate optical pathways of different refractive powers. Accommodation is most commonly measured using IR photoretinoscopy , which uses reflection of IR light from the fundus to measure dynamic changes in the refractive error. Since mammalian accommodation is mediated by contraction of the smooth ciliary muscle, it can be stimulated by pilocarpine. Humans and other primates accommodate by changing the curvature of the lens ( Figure 2.12). To view distant objects, sympathetic innervation induces relaxation of the ciliary body muscle, which in turn leads to stretching of the lens zonule. The increased tension of the zonules results in a greater pull on the lens capsule, thus causing the lens to become more discoid and decreasing its overall axial thickness and refractive power in a process of disaccommodation . To accommodate for near objects, the reverse process takes place. Parasympathetic input induces contraction of the ciliary body muscles, leading to relaxation of the zonular fibers and reduced tension on the lens capsule. In turn, this liberates the inherent elasticity of the lens, resulting in a more spherical lens possessing greater axial thickness and refractive power. Consequently, anterior chamber depth decreases and increases during accommodation and disaccommodation, respectively.
Читать дальше