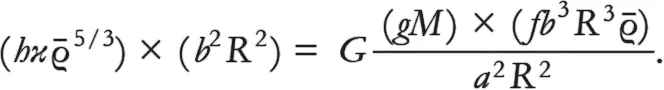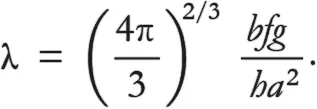Джефф Форшоу - Квантовая вселенная. Как устроено то, что мы не можем увидеть

Второй соавтор считает более четким следующее разъяснение: « f может в принципе по-разному сложным образом зависеть от r – расстояния кубика от центра звезды. Но давайте представим, что эти величины прямо пропорциональны, то есть f ∝ r . Иными словами, f = Br , где B – константа. Здесь самое важное то, что f – чисто численный показатель, в то время как r измеряется, например, в метрах. Отсюда следует, что B должно измеряться в 1/м, чтобы единицы расстояния взаимно сокращались. Итак, что нужно выбрать для B ? Мы не можем назначить нечто произвольное, например «1 обратный метр», поскольку это бессмысленно и никак не связано со звездой. Почему, например, не выбрать один обратный световой год, получив совершенно другой ответ? Единственное расстояние, с которым мы имеем дело, – это R , физический радиус звезды, так что придется использовать его, чтобы f всегда оставалось чистым числом. Это значит, что f может зависеть только от r / R . Вы, наверное, уже поняли, что тот же вывод можно было сделать, если бы мы начали с предположения, что, например, f ∝ r ²». Собственно, ровно то же говорил и первый соавтор, только сейчас вышло длиннее.

Это значит, что можно выразить массу нашего кубика размером L и объемом L ³, находящегося на расстоянии r от центра звезды, в виде Mcube = f(a)L ³ ρ̅ . Мы написали f(a) , а не просто f , чтобы не забывать, что f на деле зависит от нашего выбора a = r / R , а не от каких-то масштабных свойств звезды. Тот же аргумент можно использовать при указании, что мы можем записать Min = g(a)M , где g(a) – это опять же только функция от a . Например, функция g(a) , высчитанная для a = ½, подсказывает, какое количество массы звезды приходится на сферу с радиусом, равным половине радиуса всей звезды, и это количество неизменно для всех белых карликов независимо от их радиуса по причине, приведенной в предыдущем абзаце [61]. Вы могли заметить, что мы постоянно избавляемся от тех символов, которые встречаются в уравнении (1), заменяя их безразмерными величинами ( a, b, f и g ), помноженными на величины, зависящие только от массы и радиуса звезды (средняя плотность звезды определяется через M и R , поскольку ρ̅ = M / V и V = 4 πR ³ / 3, объем сферы). В довершение нужно сделать то же самое для разницы давлений, которую мы благодаря уравнению (4) можем записать как Pbottom – Ptop = = h(a, b)κρ̅ 5/3, где h(a, b) – безразмерная величина. То, что h(a, b) зависит одновременно от a и b , связано с тем, что разница давлений зависит не только от местоположения куба (представленного a ), но и от его объема (представленного b ): у более крупных кубов больше разница давлений. Самое важное здесь то, что, как и f(a) , и g(a), h(a, b) не может зависеть от радиуса звезды.

Мы можем воспользоваться только что выведенными выражениями и переписать уравнение (1):

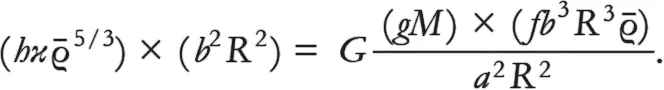
Кажется, что в уравнении царит хаос; непохоже, чтобы уже на следующей странице мы пришли к результату. Главное – заметить, что уравнение выражает отношения между массой звезды и ее радиусом – конкретная зависимость между ними уже нащупывается (или на виду, но чудовищно далека – в зависимости от вашего уровня владения математикой). После введения в наше хаотическое уравнение средней плотности звезды (то есть ρ̅ = M / (4πR ³ / 3) ) оно принимает следующий вид:

где

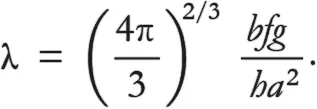
Теперь λ зависит только от безразмерных величин a, b, f, g и h , а следовательно, не зависит от величин, которые описывают звезду в целом, M и R , а следовательно, λ должна иметь одно и то же значение для всех белых карликов.

Если вас интересует, что произойдет, если изменить a и/или b (то есть изменить местоположение и/или размеры нашего кубика), то вы упустили главное в наших аргументах. Если понимать буквально, кажется, что изменение a и b изменит и λ , так что мы получим другой результат для RM ⅓. Но ведь это невозможно, так как известно, что RM ⅓зависит от самой звезды, а не от конкретных свойств того кубика, который мы придумали (или не придумали).