Джефф Форшоу - Квантовая вселенная. Как устроено то, что мы не можем увидеть

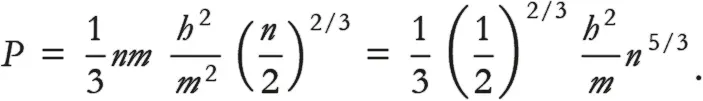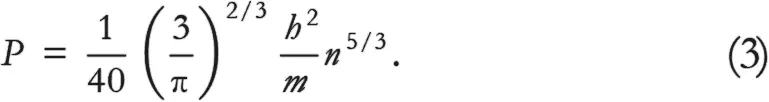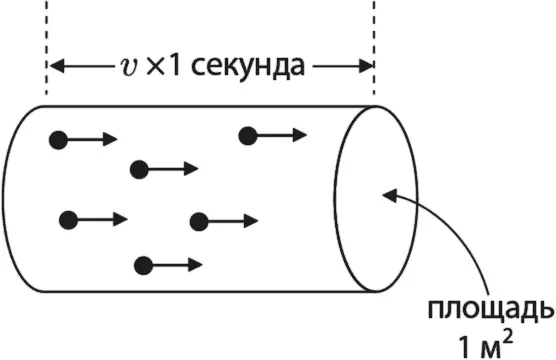
Рис. 12.4. Флот электронов (маленькие точки), движущийся в едином направлении. Все электроны в трубке такого размера будут ежесекундно ударяться о зеркало

Мы знаем это, потому что все электроны, удаленные от зеркала на расстояние v × 1 с, будут ежесекундно врезаться в зеркало. Это относится ко всем электронам в трубке, изображенной на рисунке. Поскольку объем цилиндра равен площади его поперечного сечения, помноженной на длину, то объем трубки равен v м³, а поскольку во флоте электронов на 1 м³ приходится n электронов, значит, ежесекундно в зеркало врезается nv электронов.

Когда каждый электрон отскакивает от зеркала, он получает обратный импульс, то есть каждый электрон изменяет свой импульс на величину 2 mv . Сила требуется как для того, чтобы остановить движущийся автобус и отправить его в противоположном направлении, так и для поворота импульса электрона. И тут вновь в игру вступает Исаак Ньютон. В главе 1 мы записали его второй закон в виде F = ma , но вообще-то это частный случай более общего правила, которое гласит, что сила равна изменению импульса [59]. Итак, все электроны прикладывают к зеркалу общую силу F = 2 mv × (nv) , потому что именно таково общее ежесекундное изменение импульса электронов. Благодаря тому, что пучок электронов имеет площадь 1 м², таково же будет и давление, оказываемое всеми электронами на зеркало.

От пучка электронов до газа, состоящего из электронов, лишь маленький шаг. Мы должны теперь учесть, что не все электроны движутся в одном направлении: какие-то движутся вверх, какие-то вниз, какие-то направо, какие-то налево и т. д. В результате мы должны разделить давление, оказываемое в любом направлении, на 6 (вспомните о шести гранях куба). Получится ( 2 mv) × (nv) / 6 = nmv ² / 3. В этом уравнении v можно заменить типичными скоростями движения электронов, которые мы получили в предыдущем уравнении (2) благодаря принципу неопределенности Гейзенберга, и вычислить общую величину давления, которое оказывают электроны в звезде – белом карлике [60]:

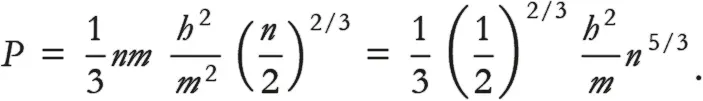
Если помните, мы предупреждали, что это приблизительный результат. Полный результат, для которого требуется гораздо больше математики, таков:

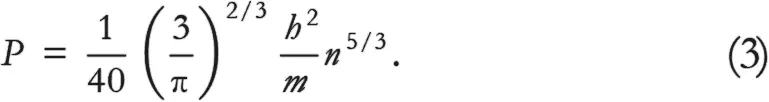
Это отличный результат. Он говорит, что давление в некотором месте звезды варьируется пропорционально количеству электронов на единицу объема в этом месте, возведенном в степень 5/3. Не беспокойтесь о том, что мы не получили константу пропорциональности в этих приблизительных расчетах, – важно, что все сошлось. Мы тем самым сказали также, что наша оценка импульса электронов, вероятно, чуть завышена, что объясняет, почему наша оценка давления оказалась выше истинного значения.

Выражение давления через плотность электронов – хорошее начало, но нашим целям лучше соответствовало бы выразить его через истинную плотность звезды. Это можно сделать, высказав на редкость безопасное предположение, что подавляющее большинство массы звезды приходится на ядра, а не на электроны (масса протона примерно в 2000 раз больше массы электрона). Мы знаем также, что количество электронов в звезде должно равняться количеству протонов, потому что звезда электрически нейтральна. Чтобы получить массовую плотность, мы должны знать, сколько протонов и нейтронов приходится на 1 м³ звезды, при этом о нейтронах забывать нельзя, так как это побочный продукт процесса синтеза. У более легких белых карликов ядро в основном будет состоять из гелия-4, конечного продукта водородного синтеза, а следовательно, количество нейтронов и протонов будет одинаковым. Теперь немного об условных обозначениях. Номер атомной массы А условно используется для обозначения числа протонов и нейтронов в ядре. Для гелия-4 А = 4.

Количество протонов в ядре мы обозначим буквой Z , для гелия Z = 2. Теперь можем выразить отношение между плотностью электронов n и массовой плотностью ρ :

и мы предположили, что масса протона, m p , равна массе нейтрона, что вполне достаточно для наших целей.