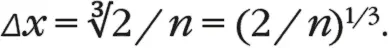Джефф Форшоу - Квантовая вселенная. Как устроено то, что мы не можем увидеть

Мы можем зайти еще дальше, потому что можно применить принцип неопределенности Гейзенберга для вычисления типичного импульса электрона. Например, если мы ограничиваем электрон областью размера Δx , он будет совершать скачки с типичным импульсом p ~ h / Δx . Собственно, как мы говорили в главе 4, импульс приблизится к верхнему пределу, а типичный импульс будет равняться чему-то от нуля до этого значения; запомните эту информацию, она понадобится нам позже. Знание импульса позволяет немедленно узнать еще две вещи. Во-первых, если электроны не подчиняются принципу Паули, то они будут ограничены областью не размера Δx , а гораздо большего размера. Это, в свою очередь, означает гораздо меньшее количество колебаний, а чем меньше колебаний, тем меньше давление. Итак, очевидно, что принцип Паули входит в игру; он настолько давит на электроны, что те, в соответствии с принципом неопределенности Гейзенберга, демонстрируют избыточные колебания. Через некоторое время мы преобразуем идею избыточных колебаний в формулу давления, но сначала узнаем, что же будет «во-вторых». Так как импульс p = mv , то скорость колебаний тоже имеет обратную зависимость от массы, так что электроны прыгают туда-сюда гораздо быстрее, чем более тяжелые ядра, которые тоже часть звезды. Вот почему давление атомных ядер пренебрежимо мало.

Итак, как можно, зная импульс электрона, вычислить давление, которое оказывает состоящий из этих электронов газ? Для начала нужно выяснить, какого размера должны быть блоки, содержащие пары электронов. Наши маленькие блоки имеют объем ( Δx )³, и, поскольку мы должны разместить все электроны внутри звезды, выразить это можно в виде числа электронов внутри звезды ( N ), деленного на объем звезды ( V ). Чтобы поместились все электроны, понадобится ровно N / 2 контейнеров, поскольку в каждом контейнере может располагаться два электрона. Это значит, что каждый контейнер будет занимать объем V , деленный на N / 2, то есть 2( V / N ). Нам неоднократно понадобится величина N / V (количество электронов на единицу объема внутри звезды), так что присвоим ей собственный символ n . Теперь можно записать, каким должен быть объем контейнеров, чтобы в нем поместились все электроны звезды, то есть ( Δx )³ = 2 / n . Извлечение кубического корня из правой части уравнения дает возможность вывести, что

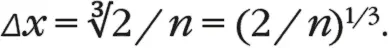
Теперь можно соотнести это с нашим выражением, полученным из принципа неопределенности, и вычислить типичный импульс электронов в соответствии с их квантовыми колебаниями:

где знак ~ означает «примерно равно». Разумеется, уравнение не может быть точным, потому что все электроны никак не могут колебаться одинаково: одни будут двигаться быстрее типичного значения, другие медленнее. Принцип неопределенности Гейзенберга не способен точно сказать, сколько электронов движутся с одной скоростью, а сколько с другой. Он дает возможность сделать более приблизительное утверждение: например, если сжать область электрона, то он будет колебаться с импульсом, примерно равным h / Δx . Мы возьмем этот типичный импульс и положим его одинаковым для всех электронов. Тем самым немного потеряем в точности вычислений, но существенно выиграем в простоте, а физика явления определенно останется той же самой [58].

Теперь мы знаем скорость электронов, что дает достаточно информации для определения давления, которое они оказывают на наш кубик. Чтобы убедиться в этом, представьте, как целый флот электронов движется в одном и том же направлении с одной и той же скоростью ( v ) по направлению к прямому зеркалу. Они ударяются о зеркало и отскакивают, двигаясь все с той же скоростью, но на сей раз в обратном направлении. Давайте вычислим силу, с которой электроны действуют на зеркало. После этого можно перейти к более реалистичным вычислениям для случаев, когда электроны двигаются в разных направлениях. Такая методология очень распространена в физике: сначала стоит поразмыслить над более простым вариантом задачи, которую хочешь решить. Тем самым можно разобраться в физике явления с меньшими проблемами и обрести уверенность для решения более серьезной задачи.

Представьте, что флот электронов состоит из n частиц на м³ и для простоты имеет в круглом сечении площадь 1 м², как показано на рис. 12.4. Через секунду nv электронов ударится о зеркало (если v измеряется в метрах в секунду).